概念的外延是一個集合。外延的集合指代的是概念。
所以可以把集合論(包括集合的定義和運算)看作是邏輯的形式化表示。
1.??
通過外延定義概念
A={a,b,c}
。外延中的對象與概念的關系:
a
∈
A
2.??
通過內涵定義概念
A={x|x
滿足所有內涵的條件
}
3.??
概念的運算
首先約定:空概念
?
;論域
R
:是邏輯運算的前提,是對概念進行運算和比較的范圍。
交
?
(邏輯乘),并
è
(邏輯加),差-(邏輯減),非
?
(邏輯反)
概念的運算結果可以產生新的概念,表現為知識的創新。
4.??
概念間的關系
相容關系
A
?
B
1
?
??????????
其中交叉關系:
A
?
B
ì
A
且
A
?
B
ì
B
??????????
包含關系:
A
ì
B
或
B
ì
A
??????????
全同關系
:
A=B
不相容關系
A
?
B=
?
??????????
其中矛盾關系:
A
è
B
=
R
??????????
反對關系:
A
è
B
ì
R
5.??
運算律
交換律:
A
è
B
=
B
è
A
;
A
?
B
=
B
?
A
結合律:(
A
è
B
)
è
C
=
A
è
(
B
è
C
);(
A
?
B
)
?
C
=
A
?
(
B
?
C
)
分配律:
A
è
(
B
?
C
)=
(
A
è
B
)
?
(
A
è
C
);
A
?
(
B
è
C
)=(
A
?
B
)
è
(
A
?
C
)
反演律(德摩根律):
?
(
A
è
B
)=
?
A
?
?
B
;
?
(
A
?
B
)=
?
A
è
?
B
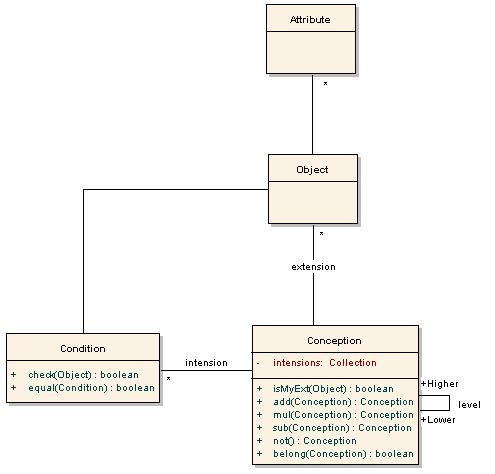
上面是數學的形式化,是針對人的。計算機并不懂這個,所以對于計算機的形式化應該反應在類的設計上:
本人的最新博客遷移到http://thinkinside.tk,使用GitHub Pages建立。
我會陸續將所寫的文章遷移過去,并進行補充和修正,
歡迎過來圍觀。




