Commons Math學習筆記——函數
看其他篇章到目錄選擇。
向量和矩陣可以說是線性代數的代表,那么返還到高等數學中,函數就是我們最常用到的單位了,還有各種微積分和其他應用,都是建立在變量、函數的基礎上的。Commons Math庫的下一個研讀部分就是針對函數這一塊。在Commons Math中也單獨有一個analysis包完成這部分實現。
縱觀analysis包中的類與接口,首先在analysis包中定義了很多函數的接口,其中主要是這幾個:UnivariateRealFunction單元實函數、BivariateRealFunction雙元實函數和MultivariateRealFunction多元實函數。其中單元和多元函數接口還有對應的矩陣函數和向量函數接口。單元和多元函數還有可微分變量函數子接口。總體來講,analysis包中的接口定義覆蓋了最常用的函數定義。比如UnivariateRealFunction只有一個成員方法那就是double value(double x),返回當前函數對應點的函數值。而如果是MultivariateRealFunction,那么它的value方法參數是一個double數組。對于繼承了UnivariateRealFunction的DifferentiableUnivariateRealFunction又添加了一個UnivariateRealFunction derivative()方法,用來返回當前函數的導數。為此,我們主要拿這個函數作為入手,來分析一些應用。關于多元函數的補充,其實多元函數在可微性上有方向導數和梯度的概念,這個在DifferentialMultivariateRealFunction中是有定義的。所以需要用到的時候,大可放心的使用相關接口定義來實現自己的函數類。
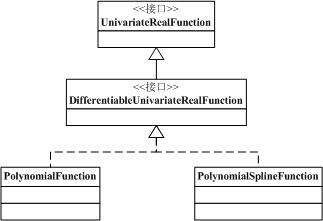
首先就是如何定義一個自己的函數類,很簡單,實現DifferentiableUnivariateRealFunction接口就夠了,然后把這兩個方法實現。舉例如下:
 public class SinFunction implements DifferentiableUnivariateRealFunction {
public class SinFunction implements DifferentiableUnivariateRealFunction {2

3
 /* Evaluate sinus fuction.
/* Evaluate sinus fuction.4
 * @see org.apache.commons.math.UnivariateRealFunction#value(double)
* @see org.apache.commons.math.UnivariateRealFunction#value(double)5
 */
*/6
 public double value(double x) throws FunctionEvaluationException {
public double value(double x) throws FunctionEvaluationException {7
 return Math.sin(x);
return Math.sin(x);8
 }
}9

10
 /* First derivative of sinus function
/* First derivative of sinus function11
 */
*/12
 public UnivariateRealFunction derivative() {
public UnivariateRealFunction derivative() {13
 return new UnivariateRealFunction() {
return new UnivariateRealFunction() {14
 public double value(double x) throws FunctionEvaluationException {
public double value(double x) throws FunctionEvaluationException {15
 return Math.cos(x);
return Math.cos(x);16
 }
}17
 };
};18
 }
}19

20
 }
}21

很顯然,這是一個正弦函數的定義。其中它的導數返回的是余弦函數,還是正確的。
定義好函數后,對于一個函數的操作運算就是相當復雜的是事情了。這次文檔只做一個關于函數的說明吧。
相關資料:
函數:http://zh.wikipedia.org/zh-cn/%E5%87%BD%E6%95%B0
Commons math包:http://commons.apache.org/math/index.html
posted on 2010-12-14 19:39 changedi 閱讀(3286) 評論(0) 編輯 收藏 所屬分類: 數學




