前文提到過(guò),除了開(kāi)方檢驗(yàn)(CHI)以外,信息增益(IG,Information Gain)也是很有效的特征選擇方法。但凡是特征選擇,總是在將特征的重要程度量化之后再進(jìn)行選擇,而如何量化特征的重要性,就成了各種方法間最大的不同。開(kāi)方檢驗(yàn)中使用特征與類別間的關(guān)聯(lián)性來(lái)進(jìn)行這個(gè)量化,關(guān)聯(lián)性越強(qiáng),特征得分越高,該特征越應(yīng)該被保留。
在信息增益中,重要性的衡量標(biāo)準(zhǔn)就是看特征能夠?yàn)榉诸愊到y(tǒng)帶來(lái)多少信息,帶來(lái)的信息越多,該特征越重要。
因此先回憶一下信息論中有關(guān)信息量(就是“熵”)的定義。說(shuō)有這么一個(gè)變量X,它可能的取值有n多種,分別是x1,x2,……,xn,每一種取到的概率分別是P1,P2,……,Pn,那么X的熵就定義為:
意思就是一個(gè)變量可能的變化越多(反而跟變量具體的取值沒(méi)有任何關(guān)系,只和值的種類多少以及發(fā)生概率有關(guān)),它攜帶的信息量就越大(因此我一直覺(jué)得我們的政策法規(guī)信息量非常大,因?yàn)樗兓芏啵境钕Ω模Γ?
對(duì)分類系統(tǒng)來(lái)說(shuō),類別C是變量,它可能的取值是C1,C2,……,Cn,而每一個(gè)類別出現(xiàn)的概率是P(C1),P(C2),……,P(Cn),因此n就是類別的總數(shù)。此時(shí)分類系統(tǒng)的熵就可以表示為:
有同學(xué)說(shuō)不好理解呀,這樣想就好了,文本分類系統(tǒng)的作用就是輸出一個(gè)表示文本屬于哪個(gè)類別的值,而這個(gè)值可能是C1,C2,……,Cn,因此這個(gè)值所攜帶的信息量就是上式中的這么多。
信息增益是針對(duì)一個(gè)一個(gè)的特征而言的,就是看一個(gè)特征t,系統(tǒng)有它和沒(méi)它的時(shí)候信息量各是多少,兩者的差值就是這個(gè)特征給系統(tǒng)帶來(lái)的信息量,即增益。系統(tǒng)含有特征t的時(shí)候信息量很好計(jì)算,就是剛才的式子,它表示的是包含所有特征時(shí)系統(tǒng)的信息量。
問(wèn)題是當(dāng)系統(tǒng)不包含t時(shí),信息量如何計(jì)算?我們換個(gè)角度想問(wèn)題,把系統(tǒng)要做的事情想象成這樣:說(shuō)教室里有很多座位,學(xué)生們每次上課進(jìn)來(lái)的時(shí)候可以隨便坐,因而變化是很大的(無(wú)數(shù)種可能的座次情況);但是現(xiàn)在有一個(gè)座位,看黑板很清楚,聽(tīng)老師講也很清楚,于是校長(zhǎng)的小舅子的姐姐的女兒托關(guān)系(真輾轉(zhuǎn)啊),把這個(gè)座位定下來(lái)了,每次只能給她坐,別人不行,此時(shí)情況怎樣?對(duì)于座次的可能情況來(lái)說(shuō),我們很容易看出以下兩種情況是等價(jià)的:(1)教室里沒(méi)有這個(gè)座位;(2)教室里雖然有這個(gè)座位,但其他人不能坐(因?yàn)榉凑膊荒軈⑴c到變化中來(lái),它是不變的)。
對(duì)應(yīng)到我們的系統(tǒng)中,就是下面的等價(jià):(1)系統(tǒng)不包含特征t;(2)系統(tǒng)雖然包含特征t,但是t已經(jīng)固定了,不能變化。
我們計(jì)算分類系統(tǒng)不包含特征t的時(shí)候,就使用情況(2)來(lái)代替,就是計(jì)算當(dāng)一個(gè)特征t不能變化時(shí),系統(tǒng)的信息量是多少。這個(gè)信息量其實(shí)也有專門的名稱,就叫做“條件熵”,條件嘛,自然就是指“t已經(jīng)固定“這個(gè)條件。
但是問(wèn)題接踵而至,例如一個(gè)特征X,它可能的取值有n多種(x1,x2,……,xn),當(dāng)計(jì)算條件熵而需要把它固定的時(shí)候,要把它固定在哪一個(gè)值上呢?答案是每一種可能都要固定一下,計(jì)算n個(gè)值,然后取均值才是條件熵。而取均值也不是簡(jiǎn)單的加一加然后除以n,而是要用每個(gè)值出現(xiàn)的概率來(lái)算平均(簡(jiǎn)單理解,就是一個(gè)值出現(xiàn)的可能性比較大,固定在它上面時(shí)算出來(lái)的信息量占的比重就要多一些)。
因此有這樣兩個(gè)條件熵的表達(dá)式:
這是指特征X被固定為值xi時(shí)的條件熵,
這是指特征X被固定時(shí)的條件熵,注意與上式在意義上的區(qū)別。從剛才計(jì)算均值的討論可以看出來(lái),第二個(gè)式子與第一個(gè)式子的關(guān)系就是:
具體到我們文本分類系統(tǒng)中的特征t,t有幾個(gè)可能的值呢?注意t是指一個(gè)固定的特征,比如他就是指關(guān)鍵詞“經(jīng)濟(jì)”或者“體育”,當(dāng)我們說(shuō)特征“經(jīng)濟(jì)”可能的取值時(shí),實(shí)際上只有兩個(gè),“經(jīng)濟(jì)”要么出現(xiàn),要么不出現(xiàn)。一般的,t的取值只有t(代表t出現(xiàn))和![]() (代表t不出現(xiàn)),注意系統(tǒng)包含t但t 不出現(xiàn)與系統(tǒng)根本不包含t可是兩回事。
(代表t不出現(xiàn)),注意系統(tǒng)包含t但t 不出現(xiàn)與系統(tǒng)根本不包含t可是兩回事。
因此固定t時(shí)系統(tǒng)的條件熵就有了,為了區(qū)別t出現(xiàn)時(shí)的符號(hào)與特征t本身的符號(hào),我們用T代表特征,而用t代表T出現(xiàn),那么:
與剛才的式子對(duì)照一下,含義很清楚對(duì)吧,P(t)就是T出現(xiàn)的概率,![]() 就是T不出現(xiàn)的概率。這個(gè)式子可以進(jìn)一步展開(kāi),其中的
就是T不出現(xiàn)的概率。這個(gè)式子可以進(jìn)一步展開(kāi),其中的
另一半就可以展開(kāi)為:
因此特征T給系統(tǒng)帶來(lái)的信息增益就可以寫(xiě)成系統(tǒng)原本的熵與固定特征T后的條件熵之差:
公式中的東西看上去很多,其實(shí)也都很好計(jì)算。比如P(Ci),表示類別Ci出現(xiàn)的概率,其實(shí)只要用1除以類別總數(shù)就得到了(這是說(shuō)你平等的看待每個(gè)類別而忽略它們的大小時(shí)這樣算,如果考慮了大小就要把大小的影響加進(jìn)去)。再比如P(t),就是特征T出現(xiàn)的概率,只要用出現(xiàn)過(guò)T的文檔數(shù)除以總文檔數(shù)就可以了,再比如P(Ci|t)表示出現(xiàn)T的時(shí)候,類別Ci出現(xiàn)的概率,只要用出現(xiàn)了T并且屬于類別Ci的文檔數(shù)除以出現(xiàn)了T的文檔數(shù)就可以了。
從以上討論中可以看出,信息增益也是考慮了特征出現(xiàn)和不出現(xiàn)兩種情況,與開(kāi)方檢驗(yàn)一樣,是比較全面的,因而效果不錯(cuò)。但信息增益最大的問(wèn)題還在于它只能考察特征對(duì)整個(gè)系統(tǒng)的貢獻(xiàn),而不能具體到某個(gè)類別上,這就使得它只適合用來(lái)做所謂“全局”的特征選擇(指所有的類都使用相同的特征集合),而無(wú)法做“本地”的特征選擇(每個(gè)類別有自己的特征集合,因?yàn)橛械脑~,對(duì)這個(gè)類別很有區(qū)分度,對(duì)另一個(gè)類別則無(wú)足輕重)。
看看,導(dǎo)出的過(guò)程其實(shí)很簡(jiǎn)單,沒(méi)有什么神秘的對(duì)不對(duì)。可有的學(xué)術(shù)論文里就喜歡把這種本來(lái)很直白的東西寫(xiě)得很晦澀,仿佛只有讀者看不懂才是作者的真正成功。
咱們是新一代的學(xué)者,咱們沒(méi)有知識(shí)不怕被別人看出來(lái),咱們有知識(shí)也不怕教給別人。所以咱都把事情說(shuō)簡(jiǎn)單點(diǎn),說(shuō)明白點(diǎn),大家好,才是真的好。


![clip_image002[4] clip_image002[4]](http://www.aygfsteel.com/images/blogjava_net/zhenandaci/WindowsLiveWriter/7fce385fe28b_D158/clip_image002%5B4%5D_thumb.gif)
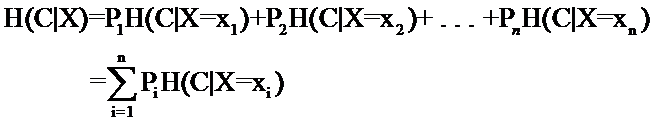
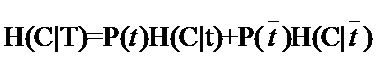
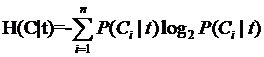

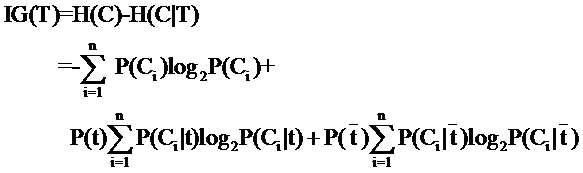


注意我說(shuō)過(guò),當(dāng)你忽略類別的大小時(shí)用1除以類別總數(shù)。您的做法是考慮了類別大小的方法。
明白了。還有一個(gè)問(wèn)題麻煩您幫忙,您列出了不少關(guān)于文本分類的參考文獻(xiàn),其中哪幾篇文獻(xiàn),特征選擇講的比較詳細(xì)?
遺憾的是基本沒(méi)有什么文獻(xiàn)會(huì)仔細(xì)的說(shuō),這可能是學(xué)術(shù)論文的通病吧,總希望讀者看不懂才好。
同感。看了不少學(xué)術(shù)論文,沒(méi)一個(gè)講明白的。弄的我在寫(xiě)程序的時(shí)候犯了不少錯(cuò)誤,例如計(jì)算信息增益的P(Ci|t)時(shí),用出現(xiàn)了T并且屬于類別Ci的“詞條數(shù)”除以出現(xiàn)了T的“詞條數(shù)”,其實(shí)應(yīng)該是“文檔數(shù)”,要不是看樓主的文章,現(xiàn)在還是這么想的,在這里,謝謝樓主了。
我也在研究特征選擇,中文學(xué)術(shù)論文對(duì)這方面寫(xiě)得感覺(jué)不大好,英文學(xué)術(shù)論文就很多比較詳細(xì)的,比如:
Y.Yang and J.Pedersen. A comparative study on feature selection in text categorization
Feature Selection for Text Categorization on Imbalanced Data
還有很多新的feature selection,我看到頭都暈了......有興趣可以發(fā)E-MAIL給我一起研究 lebee_leon@163.com
在用開(kāi)方檢驗(yàn)的方法進(jìn)行特征選擇,用LIBSVM進(jìn)行分類,訓(xùn)練數(shù)據(jù)和測(cè)試數(shù)據(jù)的accuracy是達(dá)到90%以上。但用信息增益的方法,得到模型時(shí),訓(xùn)練數(shù)據(jù)最好的結(jié)果都是90%上,但測(cè)試數(shù)據(jù)的結(jié)果卻是60%左右。我所用的數(shù)據(jù)是北大分類語(yǔ)料和SOGOU的語(yǔ)料。
博主,我想問(wèn)問(wèn),會(huì)有這么大差距,還是我的IG算錯(cuò)了?
非常期待您的回復(fù)。謝謝!
可以試試卡方檢驗(yàn)(CHI Test)。
對(duì)啊!!!
一氣看了博主的文本分類的文章,寫(xiě)的好呀
多類劃分方法的最后方案類似決策樹(shù)啊。
膜拜
看到樓主的最后一句,感覺(jué)仿佛說(shuō)出了自己的心聲。說(shuō)的好!
我算出IG較大的詞都是在文本集合中僅出現(xiàn)過(guò)一次的詞(即出現(xiàn)該特征的文檔數(shù)為1)
贊!!
有的學(xué)術(shù)論文作者可能是1號(hào)技能強(qiáng)2號(hào)技能弱,從而導(dǎo)致別人看不懂自己的文章,但并不一定是故意讓別人看不懂。。。
而博主就是兩個(gè)技能都很強(qiáng),不僅理解深刻,而且表述得通俗易懂平易近人~充滿了逆襲的潛質(zhì)^_^
“@妞妞
可以試試卡方檢驗(yàn)(CHI Test)。”就是上一篇的“開(kāi)方檢驗(yàn)”么?
這句下面的那個(gè)公式發(fā)覺(jué)特別難理解
怎么還有本地特征選擇?每個(gè)類都有自己的特征集合,還怎么classification?
這句話說(shuō)得太棒了!
P(t)是指用用出現(xiàn)過(guò)T的是訓(xùn)練集文檔除以訓(xùn)練集的總文檔數(shù)目,還是用出現(xiàn)過(guò)T的測(cè)試集文檔除以測(cè)試集的總文檔數(shù)目?
同理,P(Ci|t)表示的是指用什么文檔除數(shù)目以什么文檔數(shù)目?
困惑了好久,忘耐心解答。謝謝~