接下來要說的東西其實不是松弛變量本身，但由于是為了使用松弛變量才引入的，因此放在這里也算合適，那就是懲罰因子C。回頭看一眼引入了松弛變量以后的優化問題：

注意其中C的位置，也可以回想一下C所起的作用（表征你有多么重視離群點，C越大越重視，越不想丟掉它們）。這個式子是以前做SVM的人寫的，大家也就這么用，但沒有任何規定說必須對所有的松弛變量都使用同一個懲罰因子，我們完全可以給每一個離群點都使用不同的C，這時就意味著你對每個樣本的重視程度都不一樣，有些樣本丟了也就丟了，錯了也就錯了，這些就給一個比較小的C；而有些樣本很重要，決不能分類錯誤（比如中央下達的文件啥的，笑），就給一個很大的C。

當然實際使用的時候并沒有這么極端，但一種很常用的變形可以用來解決分類問題中樣本的“偏斜”問題。

先來說說樣本的偏斜問題，也叫數據集偏斜（unbalanced），它指的是參與分類的兩個類別（也可以指多個類別）樣本數量差異很大。比如說正類有10，000個樣本，而負類只給了100個，這會引起的問題顯而易見，可以看看下面的圖：

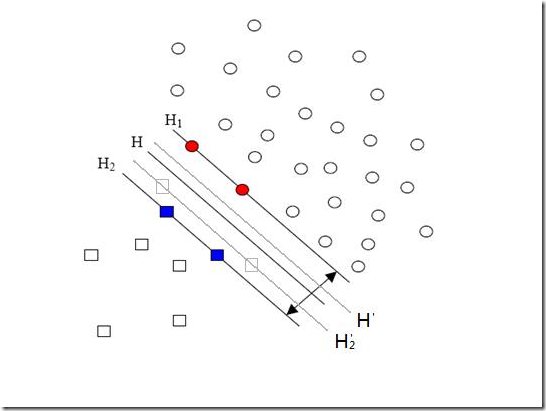
方形的點是負類。H，H₁，H₂是根據給的樣本算出來的分類面，由于負類的樣本很少很少，所以有一些本來是負類的樣本點沒有提供，比如圖中兩個灰色的方形點，如果這兩個點有提供的話，那算出來的分類面應該是H’，H₂’和H₁，他們顯然和之前的結果有出入，實際上負類給的樣本點越多，就越容易出現在灰色點附近的點，我們算出的結果也就越接近于真實的分類面。但現在由于偏斜的現象存在，使得數量多的正類可以把分類面向負類的方向“推”，因而影響了結果的準確性。

對付數據集偏斜問題的方法之一就是在懲罰因子上作文章，想必大家也猜到了，那就是給樣本數量少的負類更大的懲罰因子，表示我們重視這部分樣本（本來數量就少，再拋棄一些，那人家負類還活不活了），因此我們的目標函數中因松弛變量而損失的部分就變成了：

其中i=1…p都是正樣本，j=p+1…p+q都是負樣本。libSVM這個算法包在解決偏斜問題的時候用的就是這種方法。

那C₊和C_-怎么確定呢？它們的大小是試出來的（參數調優），但是他們的比例可以有些方法來確定。咱們先假定說C₊是5這么大，那確定C_-的一個很直觀的方法就是使用兩類樣本數的比來算，對應到剛才舉的例子，C_-就可以定為500這么大（因為10，000：100=100：1嘛）。

但是這樣并不夠好，回看剛才的圖，你會發現正類之所以可以“欺負”負類，其實并不是因為負類樣本少，真實的原因是負類的樣本分布的不夠廣（沒擴充到負類本應該有的區域）。說一個具體點的例子，現在想給政治類和體育類的文章做分類，政治類文章很多，而體育類只提供了幾篇關于籃球的文章，這時分類會明顯偏向于政治類，如果要給體育類文章增加樣本，但增加的樣本仍然全都是關于籃球的（也就是說，沒有足球，排球，賽車，游泳等等），那結果會怎樣呢？雖然體育類文章在數量上可以達到與政治類一樣多，但過于集中了，結果仍會偏向于政治類！所以給C₊和C_-確定比例更好的方法應該是衡量他們分布的程度。比如可以算算他們在空間中占據了多大的體積，例如給負類找一個超球——就是高維空間里的球啦——它可以包含所有負類的樣本，再給正類找一個，比比兩個球的半徑，就可以大致確定分布的情況。顯然半徑大的分布就比較廣，就給小一點的懲罰因子。

但是這樣還不夠好，因為有的類別樣本確實很集中，這不是提供的樣本數量多少的問題，這是類別本身的特征（就是某些話題涉及的面很窄，例如計算機類的文章就明顯不如文化類的文章那么“天馬行空”），這個時候即便超球的半徑差異很大，也不應該賦予兩個類別不同的懲罰因子。

看到這里讀者一定瘋了，因為說來說去，這豈不成了一個解決不了的問題？然而事實如此，完全的方法是沒有的，根據需要，選擇實現簡單又合用的就好（例如libSVM就直接使用樣本數量的比）。