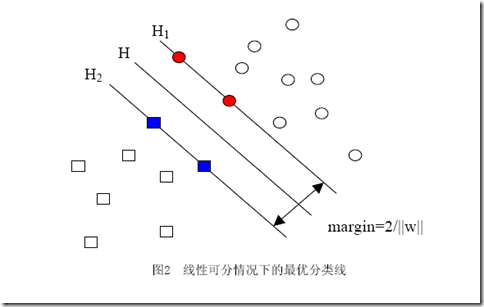
讓我再一次比較完整的重復(fù)一下我們要解決的問題:我們有屬于兩個類別的樣本點(并不限定這些點在二維空間中)若干,如圖,
圓形的樣本點定為正樣本(連帶著,我們可以把正樣本所屬的類叫做正類),方形的點定為負例。我們想求得這樣一個線性函數(shù)(在n維空間中的線性函數(shù)):
g(x)=wx+b
使得所有屬于正類的點x+代入以后有g(shù)(x+)≥1,而所有屬于負類的點x-代入后有g(shù)(x-)≤-1(之所以總跟1比較,無論正一還是負一,都是因為我們固定了間隔為1,注意間隔和幾何間隔的區(qū)別)。代入g(x)后的值如果在1和-1之間,我們就拒絕判斷。
求這樣的g(x)的過程就是求w(一個n維向量)和b(一個實數(shù))兩個參數(shù)的過程(但實際上只需要求w,求得以后找某些樣本點代入就可以求得b)。因此在求g(x)的時候,w才是變量。
你肯定能看出來,一旦求出了w(也就求出了b),那么中間的直線H就知道了(因為它就是wx+b=0嘛,哈哈),那么H1和H2也就知道了(因為三者是平行的,而且相隔的距離還是||w||決定的)。那么w是誰決定的?顯然是你給的樣本決定的,一旦你在空間中給出了那些個樣本點,三條直線的位置實際上就唯一確定了(因為我們求的是最優(yōu)的那三條,當然是唯一的),我們解優(yōu)化問題的過程也只不過是把這個確定了的東西算出來而已。
樣本確定了w,用數(shù)學(xué)的語言描述,就是w可以表示為樣本的某種組合:
w=α1x1+α2x2+…+αnxn
式子中的αi是一個一個的數(shù)(在嚴格的證明過程中,這些α被稱為拉格朗日乘子),而xi是樣本點,因而是向量,n就是總樣本點的個數(shù)。為了方便描述,以下開始嚴格區(qū)別數(shù)字與向量的乘積和向量間的乘積,我會用α1x1表示數(shù)字和向量的乘積,而用<x1,x2>表示向量x1,x2的內(nèi)積(也叫點積,注意與向量叉積的區(qū)別)。因此g(x)的表達式嚴格的形式應(yīng)該是:
g(x)=<w,x>+b
但是上面的式子還不夠好,你回頭看看圖中正樣本和負樣本的位置,想像一下,我不動所有點的位置,而只是把其中一個正樣本點定為負樣本點(也就是把一個點的形狀從圓形變?yōu)榉叫危Y(jié)果怎么樣?三條直線都必須移動(因為對這三條直線的要求是必須把方形和圓形的點正確分開)!這說明w不僅跟樣本點的位置有關(guān),還跟樣本的類別有關(guān)(也就是和樣本的“標簽”有關(guān))。因此用下面這個式子表示才算完整:
w=α1y1x1+α2y2x2+…+αnynxn (式1)
其中的yi就是第i個樣本的標簽,它等于1或者-1。其實以上式子的那一堆拉格朗日乘子中,只有很少的一部分不等于0(不等于0才對w起決定作用),這部分不等于0的拉格朗日乘子后面所乘的樣本點,其實都落在H1和H2上,也正是這部分樣本(而不需要全部樣本)唯一的確定了分類函數(shù),當然,更嚴格的說,這些樣本的一部分就可以確定,因為例如確定一條直線,只需要兩個點就可以,即便有三五個都落在上面,我們也不是全都需要。這部分我們真正需要的樣本點,就叫做支持(撐)向量!(名字還挺形象吧,他們“撐”起了分界線)
式子也可以用求和符號簡寫一下:
因此原來的g(x)表達式可以寫為:
注意式子中x才是變量,也就是你要分類哪篇文檔,就把該文檔的向量表示代入到 x的位置,而所有的xi統(tǒng)統(tǒng)都是已知的樣本。還注意到式子中只有xi和x是向量,因此一部分可以從內(nèi)積符號中拿出來,得到g(x)的式子為:
發(fā)現(xiàn)了什么?w不見啦!從求w變成了求α。
但肯定有人會說,這并沒有把原問題簡化呀。嘿嘿,其實簡化了,只不過在你看不見的地方,以這樣的形式描述問題以后,我們的優(yōu)化問題少了很大一部分不等式約束(記得這是我們解不了極值問題的萬惡之源)。但是接下來先跳過線性分類器求解的部分,來看看 SVM在線性分類器上所做的重大改進——核函數(shù)。

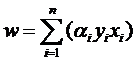
![clip_image002[4] clip_image002[4]](http://www.aygfsteel.com/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_1244A/clip_image002%5B4%5D_thumb.gif)
![clip_image002[6] clip_image002[6]](http://www.aygfsteel.com/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_1244A/clip_image002%5B6%5D_thumb.gif)


把一些在文章上看到的晦澀理論用生活化的語言展開描述
看后對我很有幫助
謝謝^_^
樓主講得太好了!你把這么深奧晦澀的東西講得如此的通俗易懂!佩服!佩服!!!
另外弱弱的問一句:“來看看 SVM在線性分類器上所做的重大改進——核函數(shù)。”是不是少打了個“非”,核函數(shù)不是用在非線性分類器上的嗎?
w=α1x1+α2x2+…+αnxn
請問,這個組合為什么一定要是線性組合呢?非線性則和行不行?
那個組合可以表示任意N維吧,如果是二維就只有x1,x2,3維就是X1,x2,X3
哪位網(wǎng)友可以幫忙,不盛感激!
QQ:273497633
w=α1x1+α2x2+…+αnxn'
這個也不太明白,為什么w是x的線性組合函數(shù)?
求那位可以解釋下?
無論所有樣本xi是否能組成n維(樣本維數(shù))向量的基,都可以用w=α1x1+α2x2+…+αnxn這種方式表示。
因為如果所有樣本xi只能組成k(k<n)維向量空間的基,那么我們分類問題就是在k維空間進行分類了,更直白的說樣本維數(shù)中有n-k維是不起作用的(可以理解為都為一樣的值,對分類問題完全沒有貢獻)。