從最一般的定義上說(shuō),一個(gè)求最小值的問(wèn)題就是一個(gè)優(yōu)化問(wèn)題(也叫尋優(yōu)問(wèn)題,更文縐縐的叫法是規(guī)劃——Programming),它同樣由兩部分組成,目標(biāo)函數(shù)和約束條件,可以用下面的式子表示:
約束條件用函數(shù)c來(lái)表示,就是constrain的意思啦。你可以看出一共有p+q個(gè)約束條件,其中p個(gè)是不等式約束,q個(gè)等式約束。
關(guān)于這個(gè)式子可以這樣來(lái)理解:式中的x是自變量,但不限定它的維數(shù)必須為1(視乎你解決的問(wèn)題空間維數(shù),對(duì)我們的文本分類(lèi)來(lái)說(shuō),那可是成千上萬(wàn)啊)。要求f(x)在哪一點(diǎn)上取得最小值(反倒不太關(guān)心這個(gè)最小值到底是多少,關(guān)鍵是哪一點(diǎn)),但不是在整個(gè)空間里找,而是在約束條件所劃定的一個(gè)有限的空間里找,這個(gè)有限的空間就是優(yōu)化理論里所說(shuō)的可行域。注意可行域中的每一個(gè)點(diǎn)都要求滿足所有p+q個(gè)條件,而不是滿足其中一條或幾條就可以(切記,要滿足每個(gè)約束),同時(shí)可行域邊界上的點(diǎn)有一個(gè)額外好的特性,它們可以使不等式約束取得等號(hào)!而邊界內(nèi)的點(diǎn)不行。
關(guān)于可行域還有個(gè)概念不得不提,那就是凸集,凸集是指有這么一個(gè)點(diǎn)的集合,其中任取兩個(gè)點(diǎn)連一條直線,這條線上的點(diǎn)仍然在這個(gè)集合內(nèi)部,因此說(shuō)“凸”是很形象的(一個(gè)反例是,二維平面上,一個(gè)月牙形的區(qū)域就不是凸集,你隨便就可以找到兩個(gè)點(diǎn)違反了剛才的規(guī)定)。
回頭再來(lái)看我們線性分類(lèi)器問(wèn)題的描述,可以看出更多的東西。
在這個(gè)問(wèn)題中,自變量就是w,而目標(biāo)函數(shù)是w的二次函數(shù),所有的約束條件都是w的線性函數(shù)(哎,千萬(wàn)不要把xi當(dāng)成變量,它代表樣本,是已知的),這種規(guī)劃問(wèn)題有個(gè)很有名氣的稱(chēng)呼——二次規(guī)劃(Quadratic Programming,QP),而且可以更進(jìn)一步的說(shuō),由于它的可行域是一個(gè)凸集,因此它是一個(gè)凸二次規(guī)劃。
一下子提了這么多術(shù)語(yǔ),實(shí)在不是為了讓大家以后能向別人炫耀學(xué)識(shí)的淵博,這其實(shí)是我們繼續(xù)下去的一個(gè)重要前提,因?yàn)樵趧?dòng)手求一個(gè)問(wèn)題的解之前(好吧,我承認(rèn),是動(dòng)計(jì)算機(jī)求……),我們必須先問(wèn)自己:這個(gè)問(wèn)題是不是有解?如果有解,是否能找到?
對(duì)于一般意義上的規(guī)劃問(wèn)題,兩個(gè)問(wèn)題的答案都是不一定,但凸二次規(guī)劃讓人喜歡的地方就在于,它有解(教科書(shū)里面為了嚴(yán)謹(jǐn),常常加限定成分,說(shuō)它有全局最優(yōu)解,由于我們想找的本來(lái)就是全局最優(yōu)的解,所以不加也罷),而且可以找到!(當(dāng)然,依據(jù)你使用的算法不同,找到這個(gè)解的速度,行話叫收斂速度,會(huì)有所不同)
對(duì)比(式2)和(式1)還可以發(fā)現(xiàn),我們的線性分類(lèi)器問(wèn)題只有不等式約束,因此形式上看似乎比一般意義上的規(guī)劃問(wèn)題要簡(jiǎn)單,但解起來(lái)卻并非如此。
因?yàn)槲覀儗?shí)際上并不知道該怎么解一個(gè)帶約束的優(yōu)化問(wèn)題。如果你仔細(xì)回憶一下高等數(shù)學(xué)的知識(shí),會(huì)記得我們可以輕松的解一個(gè)不帶任何約束的優(yōu)化問(wèn)題(實(shí)際上就是當(dāng)年背得爛熟的函數(shù)求極值嘛,求導(dǎo)再找0點(diǎn)唄,誰(shuí)不會(huì)啊?笑),我們甚至還會(huì)解一個(gè)只帶等式約束的優(yōu)化問(wèn)題,也是背得爛熟的,求條件極值,記得么,通過(guò)添加拉格朗日乘子,構(gòu)造拉格朗日函數(shù),來(lái)把這個(gè)問(wèn)題轉(zhuǎn)化為無(wú)約束的優(yōu)化問(wèn)題云云(如果你一時(shí)沒(méi)想通,我提醒一下,構(gòu)造出的拉格朗日函數(shù)就是轉(zhuǎn)化之后的問(wèn)題形式,它顯然沒(méi)有帶任何條件)。
讀者問(wèn):如果只帶等式約束的問(wèn)題可以轉(zhuǎn)化為無(wú)約束的問(wèn)題而得以求解,那么可不可以把帶不等式約束的問(wèn)題向只帶等式約束的問(wèn)題轉(zhuǎn)化一下而得以求解呢?
聰明,可以,實(shí)際上我們也正是這么做的。下一節(jié)就來(lái)說(shuō)說(shuō)如何做這個(gè)轉(zhuǎn)化,一旦轉(zhuǎn)化完成,求解對(duì)任何學(xué)過(guò)高等數(shù)學(xué)的人來(lái)說(shuō),都是小菜一碟啦。

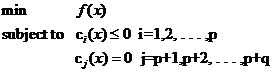
![clip_image002[5] clip_image002[5]](http://www.aygfsteel.com/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVMPart2_1603/clip_image002%5B5%5D_thumb.gif)


還賣(mài)個(gè)關(guān)子,無(wú)語(yǔ)。
你的文章深入淺出!講的太好了!!!
謝謝樓主!!!