前文提到過,除了分類算法以外,為分類文本作處理的特征提取算法也對最終效果有巨大影響,而特征提取算法又分為特征選擇和特征抽取兩大類,其中特征選擇算法有互信息,文檔頻率,信息增益,開方檢驗等等十數(shù)種,這次先介紹特征選擇算法中效果比較好的開方檢驗方法。
大家應該還記得,開方檢驗其實是數(shù)理統(tǒng)計中一種常用的檢驗兩個變量獨立性的方法。(什么?你是文史類專業(yè)的學生,沒有學過數(shù)理統(tǒng)計?那你做什么文本分類?在這搗什么亂?)
開方檢驗最基本的思想就是通過觀察實際值與理論值的偏差來確定理論的正確與否。具體做的時候常常先假設(shè)兩個變量確實是獨立的(行話就叫做“原假設(shè)”),然后觀察實際值(也可以叫做觀察值)與理論值(這個理論值是指“如果兩者確實獨立”的情況下應該有的值)的偏差程度,如果偏差足夠小,我們就認為誤差是很自然的樣本誤差,是測量手段不夠精確導致或者偶然發(fā)生的,兩者確確實實是獨立的,此時就接受原假設(shè);如果偏差大到一定程度,使得這樣的誤差不太可能是偶然產(chǎn)生或者測量不精確所致,我們就認為兩者實際上是相關(guān)的,即否定原假設(shè),而接受備擇假設(shè)。
那么用什么來衡量偏差程度呢?假設(shè)理論值為E(這也是數(shù)學期望的符號哦),實際值為x,如果僅僅使用所有樣本的觀察值與理論值的差值x-E之和
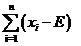
來衡量,單個的觀察值還好說,當有多個觀察值x1,x2,x3的時候,很可能x1-E,x2-E,x3-E的值有正有負,因而互相抵消,使得最終的結(jié)果看上好像偏差為0,但實際上每個都有偏差,而且都還不小!此時很直接的想法便是使用方差代替均值,這樣就解決了正負抵消的問題,即使用
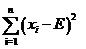
這時又引來了新的問題,對于500的均值來說,相差5其實是很小的(相差1%),而對20的均值來說,5相當于25%的差異,這是使用方差也無法體現(xiàn)的。因此應該考慮改進上面的式子,讓均值的大小不影響我們對差異程度的判斷
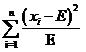 式(1)
式(1)
上面這個式子已經(jīng)相當好了。實際上這個式子就是開方檢驗使用的差值衡量公式。當提供了數(shù)個樣本的觀察值x1,x2,……xi ,……xn之后,代入到式(1)中就可以求得開方值,用這個值與事先設(shè)定的閾值比較,如果大于閾值(即偏差很大),就認為原假設(shè)不成立,反之則認為原假設(shè)成立。
在文本分類問題的特征選擇階段,我們主要關(guān)心一個詞t(一個隨機變量)與一個類別c(另一個隨機變量)之間是否相互獨立?如果獨立,就可以說詞t對類別c完全沒有表征作用,即我們根本無法根據(jù)t出現(xiàn)與否來判斷一篇文檔是否屬于c這個分類。但與最普通的開方檢驗不同,我們不需要設(shè)定閾值,因為很難說詞t和類別c關(guān)聯(lián)到什么程度才算是有表征作用,我們只想借用這個方法來選出一些最最相關(guān)的即可。
此時我們?nèi)匀恍枰靼讓μ卣鬟x擇來說原假設(shè)是什么,因為計算出的開方值越大,說明對原假設(shè)的偏離越大,我們越傾向于認為原假設(shè)的反面情況是正確的。我們能不能把原假設(shè)定為“詞t與類別c相關(guān)“?原則上說當然可以,這也是一個健全的民主主義社會賦予每個公民的權(quán)利(笑),但此時你會發(fā)現(xiàn)根本不知道此時的理論值該是多少!你會把自己繞進死胡同。所以我們一般都使用”詞t與類別c不相關(guān)“來做原假設(shè)。選擇的過程也變成了為每個詞計算它與類別c的開方值,從大到小排個序(此時開方值越大越相關(guān)),取前k個就可以(k值可以根據(jù)自己的需要選,這也是一個健全的民主主義社會賦予每個公民的權(quán)利)。
好,原理有了,該來個例子說說到底怎么算了。
比如說現(xiàn)在有N篇文檔,其中有M篇是關(guān)于體育的,我們想考察一個詞“籃球”與類別“體育”之間的相關(guān)性(任誰都看得出來兩者很相關(guān),但很遺憾,我們是智慧生物,計算機不是,它一點也看不出來,想讓它認識到這一點,只能讓它算算看)。我們有四個觀察值可以使用:
1. 包含“籃球”且屬于“體育”類別的文檔數(shù),命名為A
2. 包含“籃球”但不屬于“體育”類別的文檔數(shù),命名為B
3. 不包含“籃球”但卻屬于“體育”類別的文檔數(shù),命名為C
4. 既不包含“籃球”也不屬于“體育”類別的文檔數(shù),命名為D
用下面的表格更清晰:
|
特征選擇 |
1.屬于“體育” |
2.不屬于“體育” |
總 計 |
|
1.包含“籃球” |
A |
B |
A+B |
|
2.不包含“籃球” |
C |
D |
C+D |
|
總 數(shù) |
A+C |
B+D |
N |
如果有些特點你沒看出來,那我說一說,首先,A+B+C+D=N(這,這不廢話嘛)。其次,A+C的意思其實就是說“屬于體育類的文章數(shù)量”,因此,它就等于M,同時,B+D就等于N-M。
好,那么理論值是什么呢?以包含“籃球”且屬于“體育”類別的文檔數(shù)為例。如果原假設(shè)是成立的,即“籃球”和體育類文章沒什么關(guān)聯(lián)性,那么在所有的文章中,“籃球”這個詞都應該是等概率出現(xiàn),而不管文章是不是體育類的。這個概率具體是多少,我們并不知道,但他應該體現(xiàn)在觀察結(jié)果中(就好比拋硬幣的概率是二分之一,可以通過觀察多次拋的結(jié)果來大致確定),因此我們可以說這個概率接近
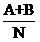
(因為A+B是包含“籃球”的文章數(shù),除以總文檔數(shù)就是“籃球”出現(xiàn)的概率,當然,這里認為在一篇文章中出現(xiàn)即可,而不管出現(xiàn)了幾次)而屬于體育類的文章數(shù)為A+C,在這些個文檔中,應該有
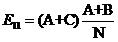
篇包含“籃球”這個詞(數(shù)量乘以概率嘛)。
但實際有多少呢?考考你(讀者:切,當然是A啦,表格里寫著嘛……)。
此時對這種情況的差值就得出了(套用式(1)的公式),應該是
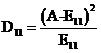
同樣,我們還可以計算剩下三種情況的差值D12,D21,D22,聰明的讀者一定能自己算出來(讀者:切,明明是自己懶得寫了……)。有了所有觀察值的差值,就可以計算“籃球”與“體育”類文章的開方值
把D11,D12,D21,D22的值分別代入并化簡,可以得到
![]()
詞t與類別c的開方值更一般的形式可以寫成
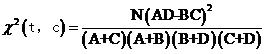 式(2)
式(2)
接下來我們就可以計算其他詞如“排球”,“產(chǎn)品”,“銀行”等等與體育類別的開方值,然后根據(jù)大小來排序,選擇我們需要的最大的數(shù)個詞匯作為特征項就可以了。
實際上式(2)還可以進一步化簡,注意如果給定了一個文檔集合(例如我們的訓練集)和一個類別,則N,M,N-M(即A+C和B+D)對同一類別文檔中的所有詞來說都是一樣的,而我們只關(guān)心一堆詞對某個類別的開方值的大小順序,而并不關(guān)心具體的值,因此把它們從式(2)中去掉是完全可以的,故實際計算的時候我們都使用
![]() 式(3)
式(3)
好啦,并不高深對不對?
針對英文純文本的實驗結(jié)果表明:作為特征選擇方法時,開方檢驗和信息增益的效果最佳(相同的分類算法,使用不同的特征選擇算法來得到比較結(jié)果);文檔頻率方法的性能同前兩者大體相當,術(shù)語強度方法性能一般;互信息方法的性能最差(文獻[17])。
但開方檢驗也并非就十全十美了。回頭想想A和B的值是怎么得出來的,它統(tǒng)計文檔中是否出現(xiàn)詞t,卻不管t在該文檔中出現(xiàn)了幾次,這會使得他對低頻詞有所偏袒(因為它夸大了低頻詞的作用)。甚至會出現(xiàn)有些情況,一個詞在一類文章的每篇文檔中都只出現(xiàn)了一次,其開方值卻大過了在該類文章99%的文檔中出現(xiàn)了10次的詞,其實后面的詞才是更具代表性的,但只因為它出現(xiàn)的文檔數(shù)比前面的詞少了“1”,特征選擇的時候就可能篩掉后面的詞而保留了前者。這就是開方檢驗著名的“低頻詞缺陷“。因此開方檢驗也經(jīng)常同其他因素如詞頻綜合考慮來揚長避短。
好啦,關(guān)于開方檢驗先說這么多,有機會還將介紹其他的特征選擇算法。
附:給精通統(tǒng)計學的同學多說幾句,式(1)實際上是對連續(xù)型的隨機變量的差值計算公式,而我們這里統(tǒng)計的“文檔數(shù)量“顯然是離散的數(shù)值(全是整數(shù)),因此真正在統(tǒng)計學中計算的時候,是有修正過程的,但這種修正仍然是只影響具體的開方值,而不影響大小的順序,故文本分類中不做這種修正。



“針對英文純文本的實驗結(jié)果表明:作為特征選擇方法時,開方檢驗和信息增益的效果最佳(相同的分類算法,使用不同的特征選擇算法來得到比較結(jié)果);文檔頻率方法的性能同前兩者大體相當,術(shù)語強度方法性能一般;互信息方法的性能最差(文獻[17])。”
這里的文獻[17]指的是哪篇文獻啊?能否透露呢?
謝謝。
我其實有一節(jié)專門列出了文本分類系列文章的參考文獻,地址是
http://www.aygfsteel.com/zhenandaci/archive/2008/05/31/204927.html
哦哦 謝謝啦
是這樣的,您稍微想一想就可以明白這代表什么樣的意義。
CHI-square 只是告訴這個特征在本類和其它類出現(xiàn)的差異大,但是沒考慮positive feature 和 negative feature 的區(qū)別。 那么實際使用,應該會用開方考慮正負那種嗎?就是CC。
不知道你是怎樣處理的?
我想說三點:
一是負特征對某些問題的分類是有幫助的,例如女性的第二性征對男性來說是負特征,但對判斷一個人是否為男性是很有幫助的,針對文本分類來說,負特征是否表征作用比正特征弱,尚沒有定論,因此不必急著剔除掉負特征.
二是負特征實際上也很容易被看出來,負特征一般特征值很大,但文檔頻率很小(因為它代表的是基本不會在某個類別出現(xiàn)的詞),我們特征選擇的時候,對每個類別也一般會先濾掉低頻詞(比如文檔頻率小于3的詞),這就剔除了很多的負特征.
三是從實驗數(shù)據(jù)的觀察來看,特征值很大的那些特征,極少有負特征,這個理論上沒有依據(jù),純粹是觀察的結(jié)果.
綜合以上三點,我個人覺得負特征不是一個很大的問題,當然如果你的系統(tǒng)追求理論上的完備性,你也可以對此做些處理.
謝謝~我按詞頻去掉詞,然后再用CHI。現(xiàn)在只用其中兩類做試驗。估計類別越多,負特征值會越小。
請問用CHI方法選擇特征時,是為每個類別分別選擇n個特征詞,再將這些特征詞的并集作為特征集好呢?
還是使用特征在各類的chi平均值或者在各類的chi中的最大值作為特征的chi值,然后為所有類別選擇一個特征集 好呢?
因為我后面分類想采用余弦夾角計算相似性,所有希望特征集在各類分布平衡。
和朋友討論后覺得全部類別要有共同的特征空間才行,不然算出來的分類分值不可比
非常誠摯的感謝樓主的博客 !!!
the bset wishes to u!!!
以后還要請教樓主
wuxinglec@gmail.com
屬于娛樂(不屬于體育) 不屬于娛樂(即屬于體育)
包含籃球 B A
不包含籃球 D C
此時計算籃球?qū)儆趭蕵返钠睿?br>(B*C-A*D)平方/(B+A)*(D+C)
計算出來的結(jié)果與體育的一樣,難道認為是籃球在娛樂的開方差和體育的一樣?
這個明顯不合理吧。
如果把籃球?qū)儆隗w育這項改成籃球?qū)儆趭蕵罚椅覀兊奈谋編熘兄挥袃纱箢悾后w育和娛樂。此時相當于第一列與第二列互換位置。
屬于娛樂(不屬于體育) 不屬于娛樂(即屬于體育)
包含籃球 B A
不包含籃球 D C
此時計算籃球?qū)儆趭蕵返钠睿?
(B*C-A*D)平方/(B+A)*(D+C)
計算出來的結(jié)果與體育的一樣,難道認為是籃球在娛樂的開方差和體育的一樣?
這個明顯不合理吧。
你這種調(diào)換方法,把A、B、C、D當成了具體而固定的數(shù)值了啊,如果按照你的這種調(diào)換方法,那么具體數(shù)值就應該變成了E、F、G、H了!沒有問題的!
@tayoto 你好,請問有沒有CHI降維的代碼呢?急求!!!
是這樣 我現(xiàn)在手頭有7200個英文訓練實例,已經(jīng)表示成SVM處理結(jié)果格式的稀疏向量,我想把它降維,聽說CHI很好 但一直沒有找到代碼,求大神幫忙,謝謝!!!
然后對理論進行測試,選擇了體育和財經(jīng)類文本各2000個,計算每個詞的開方值,并進行排序,排名前100的關(guān)鍵詞都是可以比較明顯的區(qū)分出來體育和財經(jīng),如
比賽 : 1925336.1463778939
公司 : 1792009.8901098901
市場 : 1409668.361302083
投資 : 1401629.0638730482
機構(gòu) : 1203529.0682012895
內(nèi)容 : 1074252.9817527514
證券 : 1054598.6955138403
元 : 1040272.8905646354
股 : 1035498.2547543725
風險 : 996436.4432277336
球隊 : 924064.2392314844
.
.
.
那么是否可以理解這100個特征詞只是能夠更容易的區(qū)分出文檔是否屬于某個類別?而并不能證明該文檔一定屬于該類別?如果想要得到最能證明文檔的所屬類別的關(guān)鍵詞應該如何去做呢?
1,E=10,A=15
2,E=100,A=120
兩種情況下,其實情況2的相關(guān)性不高,但計算出來的結(jié)果為:
1,2.5
2,4
第二種情況的相關(guān)性反而比第一種高。
D11為 籃球&體育 的相關(guān)性;D12為 籃球&非體育 的相關(guān)性;...;以此類推。
你說得對
我想問下,關(guān)于特征數(shù)目的選擇如何確定啊?如何評價特征選擇的好壞?
如果只有體育和娛樂兩種,那么二者就是完全依賴關(guān)系(單標簽情況下)屬于體育 ->不屬于娛樂,屬于娛樂->不屬于體育,那么籃球和體育的關(guān)聯(lián)度自然與籃球和娛樂的關(guān)聯(lián)度是一樣的。