深入理解動態規劃的一系列問題(12)
今天介紹三個經典問題,為什么直接來三個?大概是因為這三個問題我覺得太經典了,以至于在任何人學習任何語言時都可能要實現這些題目的編程訓練,所以這里就放到一起,打包講下求解這些問題的動態規劃思路(雖然有些問題不是那么直觀的動態規劃解)。
第一個問題是編輯距離(Edit Distance Problem)EDP問題,這個問題在維基上有全面的解釋,并附有準確的代碼實現(也叫levenshtein距離),我這里就簡單講下遞歸的DP解法。編輯距離需要一些前置條件,首先是距離的定義:對于兩個字符串x和y,其中x包含m個字符,y包含n個字符,目標是由x串經過一系列允許的操作后變到y串,這些操作包括:1)刪除操作D,刪掉任意一個字符,成本為c(D);2)插入操作I,插入任意一個字符,成本為c(I);3)替換操作R,替換掉字符串中的一個字符,成本為c(R)。當然變為y串后要求變化成本最優。這就是一個典型的DP問題了。定義狀態(i,j)為x串的前i個字符(即i串前綴),y串的j串前綴,于是DPFE為: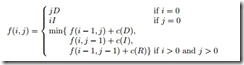 。換種表達就是
。換種表達就是![]() ,轉移函數t表示如下:
,轉移函數t表示如下: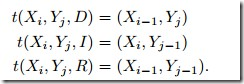 。目標就是計算f(x,y)。
。目標就是計算f(x,y)。
舉例來說:x="CAN”,y=”ANN”,三種操作的成本均為1,求x和y的編輯距離。(答案為2,具體求解見下面代碼)
源碼求解:
1: /*
2: * Copyright (C) 2013 changedi
3: *
4: * Licensed under the Apache License, Version 2.0 (the "License");
5: * you may not use this file except in compliance with the License.
6: * You may obtain a copy of the License at
7: *
8: * http://www.apache.org/licenses/LICENSE-2.0
9: *
10: * Unless required by applicable law or agreed to in writing, software
11: * distributed under the License is distributed on an "AS IS" BASIS,
12: * WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
13: * See the License for the specific language governing permissions and
14: * limitations under the License.
15: */
16: package com.jybat.dp;
17: 18: //EditDistanceProblem;
19: public class EDP {
20: 21: private static String s1 = "CAN";
22: private static String s2 = "ANN";
23: private static final int insertionCost = 1;
24: private static final int deletionCost = 1;
25: private static final int replacementCost = 1;
26: // it is useful to have the string lengths as symbolic constants
27: private static int s1Length = s1.length();
28: private static int s2Length = s2.length();
29: 30: // The decision space is constant in this example.
31: // It does not depend on the current state.
32: // We chose to code the 3 allowed operations
33: // as follows:
34: // 1 stands for delete
35: // 2 stands for insert
36: // 12 stands for replace
37: private static int[] decisionSet = { 1, 2, 12 };
38: 39: // costOfOperation()
40: // returns 0 if the specified characters in the 2 strings
41: // match and the decision is to perform
42: // "replacement" operation for matching chars
43: // (whose cost is usually defined as 0)
44: // returns 1 otherwise (if delete, insert, or a real replacement operation
45: // happens)
46: private static int costOfOperation(int i, int j, int dec) {
47: if (dec == 12) { // dec==12 means decision is to replace
48: if (s1.charAt(i - 1) // note: subtract 1 because array
49: // starts at index 0
50: == s2.charAt(j - 1)) { // matching chars, cost is 0
51: return 0;
52: } else { // real replacement
53: return replacementCost; // cost of real replacement
54: } 55: }56: if (dec == 1) { // dec==1 means decision is to delete
57: return deletionCost;
58: }59: // otherwise it must be that dec==2, decision to insert
60: return insertionCost;
61: } 62: 63: private static int s1Adjustment(int dec) {
64: if (dec == 2) { // insert
65: return 0;
66: }67: return 1;
68: } 69: 70: private static int s2Adjustment(int dec) {
71: if (dec == 1) { // delete
72: return 0;
73: }74: return 1;
75: } 76: 77: public static int d(int i, int j) {
78: if (i == 0)
79: return j;
80: if (j == 0)
81: return i;
82: int min = Integer.MAX_VALUE;
83: for (int dec : decisionSet) {
84: int t = costOfOperation(i, j, dec)
85: + d(i - s1Adjustment(dec), j - s2Adjustment(dec));86: if (t < min)
87: min = t; 88: }89: return min;
90: } 91: 92: /**
93: * @param args
94: */
95: public static void main(String[] args) {
96: System.out.println(d(s1Length, s2Length)); 97: 98: } 99: 100: }第二個問題是大家非常熟悉的斐波那契數列問題Fibonacci Recurrence Relation (FIB):
斐波那契數列就是一個經典的f(n)=f(n-1)+f(n-2)的遞歸問題。這里不講,只是列出這個問題。
第三個問題是漢諾塔問題Tower of Hanoi Problem (HANOI):
漢諾塔的問題描述就省去了,主要是定義狀態,我們定義在移動了i個碟子后的最優步數為f(i),則f(i)=2f(i-1)+1,即通用的漢諾塔策略:將碟子先移動到中間柱,移動i-1個后,將第i個碟子移動到目標柱,然后再重復將i-1個柱子以同樣的方法放回目標柱,于是這個dp方程就可以理解了。但是這樣子的方程看上去總不像動態規劃那明細的階段和狀態的對應,于是我們修正一下方程如下:f(m,i,j,k)=opt {f(m-1,i,k,j)+f(1,i,j,k)+f(m-1,k,j,i)}。狀態(m,i,j,k)表示把m個碟子從i移動到j的最優步數,k代表中間那個柱。
DP源碼如下:
1: /*
2: * Copyright (C) 2013 changedi
3: *
4: * Licensed under the Apache License, Version 2.0 (the "License");
5: * you may not use this file except in compliance with the License.
6: * You may obtain a copy of the License at
7: *
8: * http://www.apache.org/licenses/LICENSE-2.0
9: *
10: * Unless required by applicable law or agreed to in writing, software
11: * distributed under the License is distributed on an "AS IS" BASIS,
12: * WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
13: * See the License for the specific language governing permissions and
14: * limitations under the License.
15: */
16: package com.jybat.dp;
17: 18: //tower of hanoi problem
19: //Compute the number of moves when the recursive
20: //strategy is used.
21: public class HANOI {
22: 23: // m: number of disks to move
24: // i: index of source tower
25: // j: index of destination tower
26: // k: index of temporary tower
27: public static int f(int m, int i, int j, int k) {
28: if (m == 1)
29: return 1;
30: return f(m - 1, i, k, j) + f(1, i, j, k) + f(m - 1, k, j, i);
31: } 32: 33: /**
34: * @param args
35: */
36: public static void main(String[] args) {
37: System.out.println(f(3,1,2,3)); 38: } 39: 40: }總結下,其實這三個問題,除了編輯距離外,fib和hanoi都更像是遞歸教學而不是DP,但是其實從問題的結構上講,hanoi這樣的是典型的動態規劃求解,只不過過多的教科書和經驗把它們放到了遞歸里,同時又忽略了遞歸和DP的聯系。所以我這里把它們放到一起,用來說明動態規劃問題也包含經典的遞歸問題的。
posted on 2014-05-27 10:38 changedi 閱讀(1875) 評論(0) 編輯 收藏 所屬分類: 算法

