先來復習一下概率論的基礎知識：
n 個數，從中取 m 個進行進行排列，有多少中排法。
如果不同位置可以重復：
第 1 個位置有 n 種選法
第 2 個位置有 n 種選法
......
第 m 個位置有 n 種選法
根據乘法原理：總共 n**m 種排法
如果不能重復
第 1 個位置有 n 種選法
第 2 個位置有 n-1 種選法
......
第 m 個位置有 n-m+1 種選法
根據乘法原理：
總共 n*(n-1)*....*(n-m+1)種排法
全排列就是 n! 種排法 |
|
|
如果我們要編程生成所有的排列，基本上都是嵌套循環
假如 list 有 n 個元素，從中選 2 個進行排列，偽代碼基本如下
for i=0 to list.length-1
for j=0 to list.length-1{
//找到一種排列方法
temp=list[i,j]
//根據情況排除重復
..
}
問題是上面的例子，我們知道選 2 個元素排列，所以循環是 2 層。
但是，如果我們求得是 P(list,n)，n 并不確定，我們不知道循環是幾層，要想寫一個通用的函數，只能借鑒上面的思想，但是不能使用上面的形式
我的想法是：
1、用一個數組 repeat[] 來保存每層的循環變量：repeat[0] 保存第 0 層循環變量的位置，repeat[1] 保存第 1 層循環變量的位置......repeat[n-1] 保存第 n-1 層循環變量的位置
2、標記當前正在第幾層循環：layer
3、集合長度已知 ：size = list.length
4、臨時數組：temp[]，長度為 n
3、算法描述如下：
循環體（layer == 0 且 repeat[0]== size 則退出循環）
{
如果（前 n-1 層）
{
取出該層循環變量：pos=repeat[layer]
如果 (pos 到達該層末尾，即 pos==size)
{
temp[layer]=null
repeat[layer]=0//該層循環變量歸零
layer--//回到上一層
continue
}
否則
{
temp[layer]=list[pos]
repeat_count[layer]++//該層循環變量增加1
layer++//層數增加 1
continue
}
否則（在最內層）
{
不停改變 temp 最后一個元素，每改變一次，就得到一種新的組合，該層循環變量增加1
當最內層也到達 List 末尾：將該層循環變量歸零，回到上層
}
}
下面是我用 Python 編寫的 permutation 函數，接受三個參數
第一個參數：如果數字則返回排列數；如果是集合，則返回排列的集合
第二個參數：選幾個數排列，默認全排序
第三個參數：是否允許重復，默認不允許
例子：
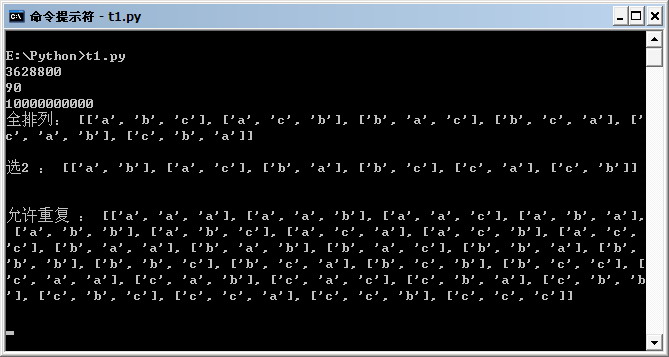
print permutation(10),'\n' #全排列數
print permutation(10,2),'\n' #10 選 2 排列數
print permutation(10,duplicate=True),'\n' #允許重復的全排列
li=['a','b','c']
print '全排列：',permutation(li),'\n'
print '選2 ：',permutation(li,2),'\n'
print '允許重復 ：',permutation(li,duplicate=True),'\n'
運行結果：
下面給出源代碼：
排列
#!/usr/bin/python
# -*- coding:GBK -*-
def permutation(arr,n=None,duplicate =False):
""" arr : 如果是數字，則返回全排列數；如果是數組，則返回全排列集合
n : 元素個數，默認全排列
duplicate: 同一個元素是否可以放在多個位置，默認不允許
注釋:如果允許元素重復，n 個位置，每個位置 size 種選法，排列數 size ** n
"""
#需要排列的數目，默認全排列
if(n==None):
if(type(arr) is int):n=arr
else:n=len(arr)
#元素數目
if(type(arr) is int):size=arr
else:size=len(arr)
if(n<1):raise Exception, 'Error: n < 1'
if(n>size):raise Exception, 'Error: n > len(arr)'
#第一個元素是數字，則返回全排列數目
if(type(arr) is int):
if(duplicate):
return size**n
else:
result=size
temp=size-1
while((size-temp)<n):
result=result*temp
temp=temp-1
return result
#循環計數器，一層一個，共 n 個，都初始化為 0
repeat_count=[0 for i in range(0,n)]
#當前正在循環的層
layer=0
#隨著計數器和層數不停變化的臨時組合,N 維數組
v_temp=[None for i in range(0,n)]
result=[]
#當前在第 0 層，且第 0 層計數器達到末尾時退出循環
while (repeat_count[0]<size) or (layer>0):
if(layer<n-1):
#小于 n-1 層
pos=repeat_count[layer]
if(pos<size):
# 層計數器 < size ，保存層計數器指向的元素，計數器前進一位，增加一層
if(not duplicate):
#不允許重復
if ((pos+1) in repeat_count):
#檢查到重復，計數器前進一位，繼續
repeat_count[layer]=repeat_count[layer]+1
continue
v_temp[layer]=arr[pos]
repeat_count[layer]=repeat_count[layer]+1
layer=layer+1
else:
# 否則，層計數器歸零，向上一層
v_temp[layer]=None
repeat_count[layer]=0
layer=layer-1
else:
#第 n-1 層：計數器每移動一個位置，都是一種組合
pos=repeat_count[layer]
if(pos<size):
if(not duplicate):
#不允許重復
if ((pos+1) in repeat_count):
#檢查到重復，計數器前進一位，繼續
repeat_count[layer]=repeat_count[layer]+1
continue
v_temp[layer]=arr[pos]
#找到一種組合，添加至結果集中
result.append([it for it in v_temp])
#層計數器前進 1 位
repeat_count[layer]=repeat_count[layer]+1
else:
# n-1 層計數器到達末尾，將層計數器歸零 ，返回上層
repeat_count[layer]=0
layer=layer-1
return result
if __name__ == "__main__":
print permutation(10),'\n' #全排列數
print permutation(10,2),'\n' #5 選 2 排列數
print permutation(10,duplicate=True),'\n' #允許重復的全排列
li=['a','b','c']
print '全排列：',permutation(li),'\n'
print '選2 ：',permutation(li,2),'\n'
print '允許重復 ：',permutation(li,duplicate=True),'\n'
raw_input()
//==========================================
posted on 2009-07-29 00:49
左洸 閱讀(1798)
評論(2) 編輯 收藏 所屬分類:
數據結構與算法