傳統的hash 算法只負責將原始內容盡量均勻隨機地映射為一個簽名值，原理上相當于偽隨機數產生算法。產生的兩個簽名，如果相等，說明原始內容在一定概 率 下是相等的；如果不相等，除了說明原始內容不相等外，不再提供任何信息，因為即使原始內容只相差一個字節，所產生的簽名也很可能差別極大。從這個意義 上來 說，要設計一個 hash 算法，對相似的內容產生的簽名也相近，是更為艱難的任務，因為它的簽名值除了提供原始內容是否相等的信息外，還能額外提供不相等的 原始內容的差異程度的信息。

而Google 的 simhash 算法產生的簽名，可以用來比較原始內容的相似度時，便很想了解這種神奇的算法的原理。出人意料，這個算法并不深奧，其思想是非常清澈美妙的。

Simhash算法

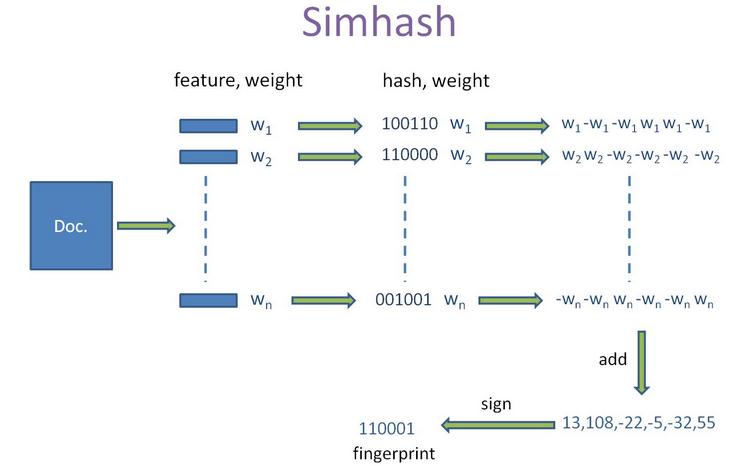
simhash算法的輸入是一個向量，輸出是一個 f 位的簽名值。為了陳述方便，假設輸入的是一個文檔的特征集合，每個特征有一定的權重。比如特征可以是文檔中的詞，其權重可以是這個詞出現的次數。 simhash 算法如下：

1，將一個 f 維的向量 V 初始化為 0 ； f 位的二進制數 S 初始化為 0 ；

2，對每一個特征：用傳統的 hash 算法對該特征產生一個 f 位的簽名 b 。對 i=1 到 f ：

如果b 的第 i 位為 1 ，則 V 的第 i 個元素加上該特征的權重；

否則，V 的第 i 個元素減去該特征的權重。 

3，如果 V 的第 i 個元素大于 0 ，則 S 的第 i 位為 1 ，否則為 0 ；

4，輸出 S 作為簽名。

算法幾何意義和原理

這個算法的幾何意義非常明了。它首先將每一個特征映射為f 維空間的一個向量，這個映射規則具體是怎樣并不重要，只要對很多不同的特征來說，它們對所對應的 向量是均勻隨機分布的，并且對相同的特征來說對應的向量是唯一的就行。比如一個特征的 4 位 hash 簽名的二進制表示為 1010 ，那么這個特征對應的  4 維向量就是 (1, -1, 1, -1) T ，即hash 簽名的某一位為 1 ，映射到的向量的對應位就為 1 ，否則為 -1 。然后，將一個文檔中所包含的各個特征對應的向量加權求和， 加權的系數等于該特征的權重。

得到的和向量即表征了這個文檔，我們可以用向量之間的夾角來衡量對應文檔之間的相似度。最后，為了得到一個 f 位的簽名，需要 進一步將其壓縮，如果和向量的某一維大于 0 ，則最終簽名的對應位為 1 ，否則為 0 。這樣的壓縮相當于只留下了和向量所在的象限這個信息，而 64 位的簽名可以 表示多達 2 64 個象限，因此只保存所在象限的信息也足夠表征一個文檔了。

比較相似度

海明距離： 兩個碼字的對應比特取值不同的比特數稱為這兩個碼字的海明距離。一個有效編碼集中, 任意兩個碼字的海明距離的最小值稱為該編碼集的海明距離。舉例如下： 10101 和 00110 從第一位開始依次有第一位、第四、第五位不同，則海明距離為 3.

異或： 只有在兩個比較的位不同時其結果是1 ，否則結果為 0 

  對每篇文檔根據SimHash 算出簽名后，再計算兩個簽名的海明距離（兩個二進制異或后 1 的個數）即可。根據經驗值，對 64 位的 SimHash ，海明距離在 3 以內的可以認為相似度比較高。

假設對64 位的 SimHash ，我們要找海明距離在 3 以內的所有簽名。我們可以把 64 位的二進制簽名均分成 4 塊，每塊 16 位。根據鴿巢原理（也成抽屜原理，見組合數學），如果兩個簽名的海明距離在 3 以內，它們必有一塊完全相同。

我們把上面分成的4 塊中的每一個塊分別作為前 16 位來進行查找。 建立倒排索引。

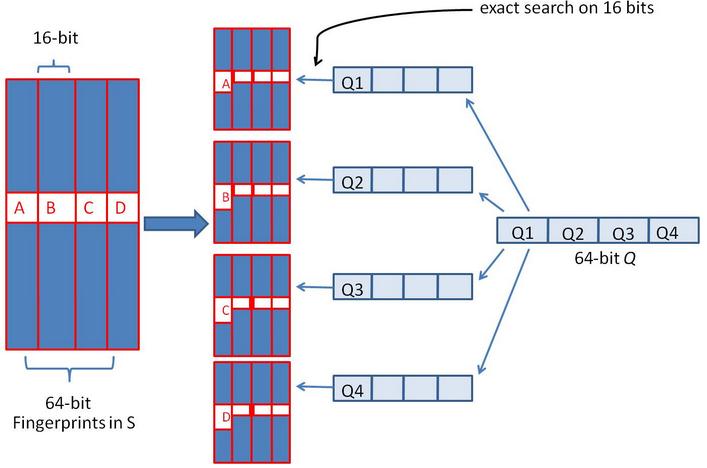
如果庫中有2^34 個（大概 10 億）簽名，那么匹配上每個塊的結果最多有 2^(34-16)=262144 個候選結果 (假設數據是均勻分布， 16 位的數據，產生的像限為 2^16 個，則平均每個像限分布的文檔數則 2^34/2^16 = 2^(34-16)) ，四個塊返回的總結果數為 4* 262144 （大概 100 萬）。原本需要比較 10 億次，經過索引，大概就只需要處理 100 萬次了。由此可見，確實大大減少了計算量。 

Java 代碼實現：

Java代碼  

1. package com.gemantic.nlp.commons.simhash;  
2.   
3. import java.math.BigInteger;  
4. import java.util.ArrayList;  
5. import java.util.List;  
6. import java.util.StringTokenizer;  
7.   
8. public class SimHash {  
9.   
10.     private String tokens;  
11.   
12.     private BigInteger intSimHash;  
13.       
14.     private String strSimHash;  
15.   
16.     private int hashbits = 64;  
17.   
18.     public SimHash(String tokens) {  
19.         this.tokens = tokens;  
20.         this.intSimHash = this.simHash();  
21.     }  
22.   
23.     public SimHash(String tokens, int hashbits) {  
24.         this.tokens = tokens;  
25.         this.hashbits = hashbits;  
26.         this.intSimHash = this.simHash();  
27.     }  
28.   
29.     public BigInteger simHash() {  
30.         int[] v = new int[this.hashbits];  
31.         StringTokenizer stringTokens = new StringTokenizer(this.tokens);  
32.         while (stringTokens.hasMoreTokens()) {  
33.             String temp = stringTokens.nextToken();  
34.             BigInteger t = this.hash(temp);  
35.             for (int i = 0; i < this.hashbits; i++) {  
36.                 BigInteger bitmask = new BigInteger("1").shiftLeft(i);  
37.                  if (t.and(bitmask).signum() != 0) {  
38.                     v[i] += 1;  
39.                 } else {  
40.                     v[i] -= 1;  
41.                 }  
42.             }  
43.         }  
44.         BigInteger fingerprint = new BigInteger("0");  
45.         StringBuffer simHashBuffer = new StringBuffer();  
46.         for (int i = 0; i < this.hashbits; i++) {  
47.             if (v[i] >= 0) {  
48.                 fingerprint = fingerprint.add(new BigInteger("1").shiftLeft(i));  
49.                 simHashBuffer.append("1");  
50.             }else{  
51.                 simHashBuffer.append("0");  
52.             }  
53.         }  
54.         this.strSimHash = simHashBuffer.toString();  
55.         System.out.println(this.strSimHash + " length " + this.strSimHash.length());  
56.         return fingerprint;  
57.     }  
58.   
59.     private BigInteger hash(String source) {  
60.         if (source == null || source.length() == 0) {  
61.             return new BigInteger("0");  
62.         } else {  
63.             char[] sourceArray = source.toCharArray();  
64.             BigInteger x = BigInteger.valueOf(((long) sourceArray[0]) << 7);  
65.             BigInteger m = new BigInteger("1000003");  
66.             BigInteger mask = new BigInteger("2").pow(this.hashbits).subtract(  
67.                     new BigInteger("1"));  
68.             for (char item : sourceArray) {  
69.                 BigInteger temp = BigInteger.valueOf((long) item);  
70.                 x = x.multiply(m).xor(temp).and(mask);  
71.             }  
72.             x = x.xor(new BigInteger(String.valueOf(source.length())));  
73.             if (x.equals(new BigInteger("-1"))) {  
74.                 x = new BigInteger("-2");  
75.             }  
76.             return x;  
77.         }  
78.     }  
79.       
80.     /** 
81.      * 取兩個二進制的異或，統計為1的個數，就是海明距離 
82.      * @param other 
83.      * @return 
84.      */  
85.   
86.     public int hammingDistance(SimHash other) {  
87.           
88.         BigInteger x = this.intSimHash.xor(other.intSimHash);  
89.         int tot = 0;  
90.           
91.         //統計x中二進制位數為1的個數  
92.         //我們想想，一個二進制數減去1，那么，從最后那個1（包括那個1）后面的數字全都反了，對吧，然后，n&(n-1)就相當于把后面的數字清0，  
93.         //我們看n能做多少次這樣的操作就OK了。  
94.           
95.          while (x.signum() != 0) {  
96.             tot += 1;  
97.             x = x.and(x.subtract(new BigInteger("1")));  
98.         }  
99.         return tot;  
100.     }  
101.   
102.     /**  
103.      * calculate Hamming Distance between two strings  
104.      *  二進制怕有錯，當成字符串，作一個，比較下結果 
105.      * @author   
106.      * @param str1 the 1st string  
107.      * @param str2 the 2nd string  
108.      * @return Hamming Distance between str1 and str2  
109.      */    
110.     public int getDistance(String str1, String str2) {    
111.         int distance;    
112.         if (str1.length() != str2.length()) {    
113.             distance = -1;    
114.         } else {    
115.             distance = 0;    
116.             for (int i = 0; i < str1.length(); i++) {    
117.                 if (str1.charAt(i) != str2.charAt(i)) {    
118.                     distance++;    
119.                 }    
120.             }    
121.         }    
122.         return distance;    
123.     }  
124.       
125.     /** 
126.      * 如果海明距離取3，則分成四塊，并得到每一塊的bigInteger值 ，作為索引值使用 
127.      * @param simHash 
128.      * @param distance 
129.      * @return 
130.      */  
131.     public List<BigInteger> subByDistance(SimHash simHash, int distance){  
132.         int numEach = this.hashbits/(distance+1);  
133.         List<BigInteger> characters = new ArrayList();  
134.           
135.         StringBuffer buffer = new StringBuffer();  
136.   
137.         int k = 0;  
138.         for( int i = 0; i < this.intSimHash.bitLength(); i++){  
139.             boolean sr = simHash.intSimHash.testBit(i);  
140.               
141.             if(sr){  
142.                 buffer.append("1");  
143.             }     
144.             else{  
145.                 buffer.append("0");  
146.             }  
147.               
148.             if( (i+1)%numEach == 0 ){  
149.                 BigInteger eachValue = new BigInteger(buffer.toString(),2);  
150.                 System.out.println("----" +eachValue );  
151.                 buffer.delete(0, buffer.length());  
152.                 characters.add(eachValue);  
153.             }  
154.         }  
155.   
156.         return characters;  
157.     }  
158.       
159.     public static void main(String[] args) {  
160.         String s = "This is a test string for testing";  
161.   
162.         SimHash hash1 = new SimHash(s, 64);  
163.         System.out.println(hash1.intSimHash + "  " + hash1.intSimHash.bitLength());  
164.           
165.         hash1.subByDistance(hash1, 3);  
166.   
167.         System.out.println("\n");  
168.         s = "This is a test string for testing, This is a test string for testing abcdef";  
169.         SimHash hash2 = new SimHash(s, 64);  
170.         System.out.println(hash2.intSimHash+ "  " + hash2.intSimHash.bitCount());  
171.         hash1.subByDistance(hash2, 3);  
172.         s = "This is a test string for testing als";  
173.         SimHash hash3 = new SimHash(s, 64);  
174.         System.out.println(hash3.intSimHash+ "  " + hash3.intSimHash.bitCount());  
175.         hash1.subByDistance(hash3, 3);  
176.         System.out.println("============================");  
177.         int dis = hash1.getDistance(hash1.strSimHash,hash2.strSimHash);  
178.           
179.         System.out.println(hash1.hammingDistance(hash2) + " "+ dis);  
180.           
181.         int dis2 = hash1.getDistance(hash1.strSimHash,hash3.strSimHash);  
182.           
183.         System.out.println(hash1.hammingDistance(hash3) + " " + dis2);  
184.           
185.   
186.   
187.     }  
188. }  

參考：   http://blog.sina.com.cn/s/blog_72995dcc010145ti.html

http://blog.sina.com.cn/s/blog_56d8ea900100y41b.html

http://blog.csdn.net/meijia_tts/article/details/7928579