使用了 G. E. P. Box、M. E. Muller 和 G. Marsaglia 的極坐標(biāo)法 (polar method)生成符合高斯分布的隨機(jī)數(shù)
1 #include <time.h>
#include <time.h>
2 #include <stdio.h>
#include <stdio.h>
3 #include <stdlib.h>
#include <stdlib.h>
4 #include <math.h>
#include <math.h>
5
6 /*生成符合0-1均勻分布的隨機(jī)數(shù)*/
/*生成符合0-1均勻分布的隨機(jī)數(shù)*/
7 double randf()
double randf()
8 {
{
9 return (double)rand()/RAND_MAX;
return (double)rand()/RAND_MAX;
10 }
}
11
12
13 /* 高斯分布隨機(jī)數(shù)生成器 */
/* 高斯分布隨機(jī)數(shù)生成器 */
14 /* 均值 m, 標(biāo)準(zhǔn)差 s */
/* 均值 m, 標(biāo)準(zhǔn)差 s */
15 double randomGaussian(double m, double s)
double randomGaussian(double m, double s)
16 {
{
17 double x1, x2, w, y1;
double x1, x2, w, y1;
18 static double y2;
static double y2;
19 static bool haveNext= false;
static bool haveNext= false;
20
21 if (haveNext)
if (haveNext)
22 {
{
23 y1 = y2;
y1 = y2;
24 haveNext = false;
haveNext = false;
25 }
}
26 else
else
27 {
{
28 do
do
29 {
{
30 x1 = 2.0 * randf() - 1.0;
x1 = 2.0 * randf() - 1.0;
31 x2 = 2.0 * randf() - 1.0;
x2 = 2.0 * randf() - 1.0;
32 w = x1 * x1 + x2 * x2;
w = x1 * x1 + x2 * x2;
33 }
}
34 while ( w >= 1.0 || w==0);
while ( w >= 1.0 || w==0);
35
36 w = sqrt( (-2.0 * log( w ) ) / w );
w = sqrt( (-2.0 * log( w ) ) / w );
37 y1 = x1 * w;
y1 = x1 * w;
38 y2 = x2 * w;
y2 = x2 * w;
39 haveNext = true;
haveNext = true;
40 }
}
41
42 return( m + y1 * s );
return( m + y1 * s );
43 }
}
44
45 void main()
void main()
46 {
{
47 srand((unsigned)time( NULL )); //初始化隨機(jī)種子
srand((unsigned)time( NULL )); //初始化隨機(jī)種子
48
49 //生成10個(gè)服從均值為0 標(biāo)準(zhǔn)差為1的高斯分布的隨機(jī)數(shù)
//生成10個(gè)服從均值為0 標(biāo)準(zhǔn)差為1的高斯分布的隨機(jī)數(shù)
50 double tmp;
double tmp;
51
52 for(int i=0;i<10;i++)
for(int i=0;i<10;i++)
53 {
{
54 tmp=randomGaussian(0,1);
tmp=randomGaussian(0,1);
55 printf("%f\n",tmp);
printf("%f\n",tmp);
56 }
}
57 }
}
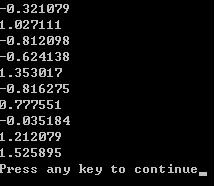
結(jié)果圖: #include <time.h>
#include <time.h>2
 #include <stdio.h>
#include <stdio.h>3
 #include <stdlib.h>
#include <stdlib.h>4
 #include <math.h>
#include <math.h>5

6
 /*生成符合0-1均勻分布的隨機(jī)數(shù)*/
/*生成符合0-1均勻分布的隨機(jī)數(shù)*/7
 double randf()
double randf()8
 {
{9
 return (double)rand()/RAND_MAX;
return (double)rand()/RAND_MAX;10
 }
}11

12

13
 /* 高斯分布隨機(jī)數(shù)生成器 */
/* 高斯分布隨機(jī)數(shù)生成器 */14
 /* 均值 m, 標(biāo)準(zhǔn)差 s */
/* 均值 m, 標(biāo)準(zhǔn)差 s */15
 double randomGaussian(double m, double s)
double randomGaussian(double m, double s) 16
 {
{ 17
 double x1, x2, w, y1;
double x1, x2, w, y1;18
 static double y2;
static double y2;19
 static bool haveNext= false;
static bool haveNext= false;20

21
 if (haveNext)
if (haveNext) 22
 {
{23
 y1 = y2;
y1 = y2;24
 haveNext = false;
haveNext = false;25
 }
}26
 else
else27
 {
{28
 do
do 29
 {
{30
 x1 = 2.0 * randf() - 1.0;
x1 = 2.0 * randf() - 1.0;31
 x2 = 2.0 * randf() - 1.0;
x2 = 2.0 * randf() - 1.0;32
 w = x1 * x1 + x2 * x2;
w = x1 * x1 + x2 * x2;33
 }
}34
 while ( w >= 1.0 || w==0);
while ( w >= 1.0 || w==0);35

36
 w = sqrt( (-2.0 * log( w ) ) / w );
w = sqrt( (-2.0 * log( w ) ) / w );37
 y1 = x1 * w;
y1 = x1 * w;38
 y2 = x2 * w;
y2 = x2 * w;39
 haveNext = true;
haveNext = true;40
 }
}41

42
 return( m + y1 * s );
return( m + y1 * s );43
 }
}44

45
 void main()
void main()46
 {
{47
 srand((unsigned)time( NULL )); //初始化隨機(jī)種子
srand((unsigned)time( NULL )); //初始化隨機(jī)種子48

49
 //生成10個(gè)服從均值為0 標(biāo)準(zhǔn)差為1的高斯分布的隨機(jī)數(shù)
//生成10個(gè)服從均值為0 標(biāo)準(zhǔn)差為1的高斯分布的隨機(jī)數(shù)50
 double tmp;
double tmp;51

52
 for(int i=0;i<10;i++)
for(int i=0;i<10;i++)53
 {
{54
 tmp=randomGaussian(0,1);
tmp=randomGaussian(0,1);55
 printf("%f\n",tmp);
printf("%f\n",tmp);56
 }
}57
 }
}
參考:http://www.taygeta.com/random/gaussian.html






