正在播放国产精品,国严精品久久久久久亚洲影视,欧美bbbxxxxx

Mon, 04 Oct 2010 02:33:00 GMT

本文��ȝ��一�U�数据结构：跌��表。前半部分蟩跃表性质和操作的介绍直接摘自《让��法的效率蟩��h��--��谈“跌��?#8221;的相��x��作及其应用》上��市华东师范大学�W�二附属中学 ��冉。之后将附上跌��表的源代码，以及本�h对其的了解。难免有错误之处�Q�希望指正，共同�q�步。谢谢�?/font>

跌��表（Skip List�Q�是1987�q�才诞生的一�U�崭新的数据�l�构�Q�它在进行查找、插入、删除等操作时的期望旉��复杂度均为O(logn),有着�q�乎替代�q��树的本领。而且最重要的一点，��是它的�~�程复杂度较同类的AVL树，�U�黑树等要低得多�Q�这使得其无论是在理解还是在推广性上�Q�都有着十分明显的优�ѝ�?/font>

首先�Q�我们来看一下蟩跃表的结�?/font>

跌��表由多条链构成（S0�Q�S1�Q�S2 ……�Q�Sh�Q�，且满��_��下三个条�Ӟ��

每条铑ֿ��d��含两个特�D�元素：+∞ �?-∞(其实不需�?
S0包含所有的元素�Q��ƈ且所有链中的元素按照升序排列�?br /> 每条链中的元素集合必��d��含于序数较小的链的元素集合�?br /> 操作

   一、查�?br />    目的�Q�在跌��表中查找一个元素x
   在蟩跃表中查找一个元素x�Q�按照如下几个步骤进行：
      1. 从最上层的链�Q�Sh�Q�的开头开�?br />       2. 假设当前位置为p�Q�它向右指向的节点�ؓq�Q�p与q不一定相邻）�Q�且q的��gؓy。将y与x作比�?br />           (1) x=y 输出查询成功及相关信�?br />           (2) x>y 从p向右�U�d��到q的位�|?br />           (3) x

3. 如果当前位置在最底层的链中（S0�Q�，且还要往下移动的话，则输出查询失�?/font>

二、插�?br /> 目的�Q�向跌��表中插入一个元素x
首先明确�Q�向跌��表中插入一个元素，相当于在表中插入一列从S0中某一位置出发向上的连�l�一�D�元素。有两个参数需要确定，��x��入列的位�|�以及它�?#8220;高度”�?br /> 关于插入的位�|�，我们先利用蟩跃表的查扑֊�能，扑ֈ�比x��的最大的数y。根据蟩跃表中所有链均是递增序列的原则，x必然��插在y的后面�?br /> 而插入列�?#8220;高度”较前者来说显得更加重要，也更加难以确定。由于它的不��定性，使得不同的决�{�可能会��D��截然不同的算法效率。�ؓ了��插入数据之后�Q�保持该数据�l�构�q�行各种操作均�ؓO(logn)复杂度的性质�Q�我们引入随机化��法�Q�Randomized Algorithms�Q��?/font>

我们定义一个随机决�{�模块，它的大致内容如下�Q?/font>

产生一�?�?的随机数r r ← random()
如果r��于一个常数p�Q�则执行�Ҏ��A�Q?nbsp; if r

否则�Q�执行方案B else do B
初始时列高�ؓ1。插入元素时�Q�不停地执行随机决策模块。如果要求执行的是A操作�Q�则��列的高度加1�Q��ƈ且��l�反复执行随机决�{�模块。直到第i�ơ，模块要求执行的是B操作�Q�我们结束决�{�，�q�向跌��表中插入一个高度�ؓi的列�?/font>

     我们来看一个例子：
     假设当前我们要插入元�?#8220;40”�Q�且在执行了随机决策模块后得到高度�ؓ4
     步骤一�Q�找到表中比40��的最大的敎ͼ��定插入位置

步骤二：插入高度�?的列�Q��ƈ�l�护跌��表的�l�构

三、删�?/p>

目的�Q�从跌��表中删除一个元素x
删除操作分�ؓ以下三个步骤�Q?/p>

在蟩跃表中查扑ֈ��q�个元素的位�|�，如果未找刎ͼ�则退�?
��该元素所在整列从表中删除
��多余的“�I�链”删除

    我们来看一下蟩跃表的相兛_��杂度�Q?br />
       �I�间复杂度： O(n)       �Q�期望）
       跌��表高度： O(logn) �Q�期望）

    相关操作的时间复杂度�Q?br />       查找�Q?nbsp; O(logn)    �Q�期望）
      插入�Q?nbsp; O(logn)    �Q�期望）
      删除�Q?nbsp; O(logn)   �Q�期望）

    之所以在每一��后面都加一�?#8220;期望”�Q�是因�ؓ跌��表的复杂度分析是��Z��概率论的。有可能会��生最坏情况，不过�q�种概率极其微小�?/p>

--------------------------------------------------------------------------------

以下是自己学习时��到的一些问�?/p>

首先分配一个链表，用list.hdr指向�Q�长度�ؓ跌��表规定的最高层�Q�说是链表，在以下代码中只是分配了一�D�连�l�的�I�间�Q�用来指向每一层的开始位�|�。我们看到结构体nodeType中，有一个key,一个rec(用户数据)�Q�还有一个指向结构体的指针数�l��?/p>

一开始的那些囑֮�易给��解。如上图所�C�，例如每个节点的forward[2]�Q�就认�ؓ是蟩跃表的第3层。List.hdr的forward[2]指向11�Q?1的forward[2]指向30�Q?0的forward[2]指向53。这��是跌��表的�W?层：11---30-----53。（准确的说每个forward都指向新节点�Q�新节点的同层forward又指向另一个节点，从而构成一个链表，而数据只有一个，�q�不是像开始途中所�ȝ��那样有N个副本）。本人天资愚钝，看了挺长旉��才把它在内存里的�l�构看清楚了�Q�呵��c�?nbsp;

以下是在�|�上搜到的一个实��C��?/p>

代码中主要注释了insert函数�Q�剩下的两个函数差不多，��׃��一一注释�?/p>

view plaincopy to clipboardprint?
/* skip list */

#include
#include

/* implementation dependent declarations */
typedef enum {
    STATUS_OK,
    STATUS_MEM_EXHAUSTED,
    STATUS_DUPLICATE_KEY,
    STATUS_KEY_NOT_FOUND
} statusEnum;

typedef int keyType;            /* type of key */

/* user data stored in tree */
typedef struct {
    int stuff;                  /* optional related data */
} recType;

#define compLT(a,b) (a < b)
#define compEQ(a,b) (a == b)

/* levels range from (0 .. MAXLEVEL) */
#define MAXLEVEL 15

typedef struct nodeTag {
    keyType key;                /* key used for searching */
    recType rec;                /* user data */
    struct nodeTag *forward[1]; /* skip list forward pointer */
} nodeType;

/* implementation independent declarations */
typedef struct {
    nodeType *hdr;              /* list Header */
    int listLevel;              /* current level of list */
} SkipList;

SkipList list;                  /* skip list information */

#define NIL list.hdr
static int count = 0;
statusEnum insert(keyType key, recType *rec) {
    int i, newLevel;
    nodeType *update[MAXLEVEL+1];
    nodeType *x;
    count++;
   /***********************************************
    * allocate node for data and insert in list *
    ***********************************************/

    /* find where key belongs */
    /*从高层一直向下寻找，直到�q�层指针为NIL�Q�也��是�?nbsp;
    后面没有数据了，到头了，�q�且�q�个��g��再小于要插入的倹{�?nbsp;
    记录�q�个位置�Q�留着向其后面插入数据*/
    x = list.hdr;
    for (i = list.listLevel; i >= 0; i--) {
        while (x->forward[i] != NIL
          && compLT(x->forward[i]->key, key))
            x = x->forward[i];
        update[i] = x;
    }


    /*现在让X指向�W?层的X的后一个节�?/
    x = x->forward[0];


    /*如果相等��׃��用插入了*/
    if (x != NIL && compEQ(x->key, key))
        return STATUS_DUPLICATE_KEY;

   /*随机的计��要插入的值的最高level*/
    for (
      newLevel = 0;
      rand() < RAND_MAX/2 && newLevel < MAXLEVEL;
      newLevel++);
    /*如果大于当前的level�Q�则更新update数组�q�更新当前level*/
    if (newLevel > list.listLevel) {
        for (i = list.listLevel + 1; i <= newLevel; i++)
            update[i] = NIL;
        list.listLevel = newLevel;
    }

    /* �l�新节点分配�I�间�Q�分配newLevel个指针，则这�?nbsp;
    节点的高度就固定了，只有newLevel。更高的层次��?nbsp;
    不会再有�q�个�?/
    if ((x = malloc(sizeof(nodeType) + newLevel*sizeof(nodeType *))) == 0)
        return STATUS_MEM_EXHAUSTED;
    x->key = key;
    x->rec = *rec;

    /* �l�每层都加上�q�个��|��相当于往链表中插入一个数*/
    for (i = 0; i <= newLevel; i++) {
        x->forward[i] = update[i]->forward[i];
        update[i]->forward[i] = x;
    }
    return STATUS_OK;
}

statusEnum delete(keyType key) {
    int i;
    nodeType *update[MAXLEVEL+1], *x;

   /*******************************************
    * delete node containing data from list *
    *******************************************/

    /* find where data belongs */
    x = list.hdr;
    for (i = list.listLevel; i >= 0; i--) {
        while (x->forward[i] != NIL
          && compLT(x->forward[i]->key, key))
            x = x->forward[i];
        update[i] = x;
    }

    x = x->forward[0];

    if (x == NIL || !compEQ(x->key, key)) return STATUS_KEY_NOT_FOUND;

    /* adjust forward pointers */
    for (i = 0; i <= list.listLevel; i++) {
        if (update[i]->forward[i] != x) break;
        update[i]->forward[i] = x->forward[i];
    }

    free (x);

    /* adjust header level */
    while ((list.listLevel > 0)
    && (list.hdr->forward[list.listLevel] == NIL))
        list.listLevel--;

    return STATUS_OK;
}

statusEnum find(keyType key, recType *rec) {
    int i;
    nodeType *x = list.hdr;

   /*******************************
    * find node containing data *
    *******************************/

    for (i = list.listLevel; i >= 0; i--) {
        while (x->forward[i] != NIL
          && compLT(x->forward[i]->key, key))
            x = x->forward[i];
    }
    x = x->forward[0];
    if (x != NIL && compEQ(x->key, key)) {
        *rec = x->rec;
        return STATUS_OK;
    }
    return STATUS_KEY_NOT_FOUND;
}

void initList() {
    int i;

   /**************************
    * initialize skip list *
    **************************/

    if ((list.hdr = malloc(
            sizeof(nodeType) + MAXLEVEL*sizeof(nodeType *))) == 0) {
        printf ("insufficient memory (initList)\n");
        exit(1);
    }
    for (i = 0; i <= MAXLEVEL; i++)
        list.hdr->forward[i] = NIL;
    list.listLevel = 0;
}

int main(int argc, char **argv) {
    int i, maxnum, random;
    recType *rec;
    keyType *key;
    statusEnum status;

    /* command-line:
     *
     *   skl maxnum [random]
     *
     *   skl 2000
     *       process 2000 sequential records
     *   skl 4000 r
     *       process 4000 random records
     *
     */

    maxnum = 20;
    random = argc > 2;

    initList();

    if ((rec = malloc(maxnum * sizeof(recType))) == 0) {
        fprintf (stderr, "insufficient memory (rec)\n");
        exit(1);
    }
    if ((key = malloc(maxnum * sizeof(keyType))) == 0) {
        fprintf (stderr, "insufficient memory (key)\n");
        exit(1);
    }

    if (random) {
        /* fill "a" with unique random numbers */
        for (i = 0; i < maxnum; i++) key[i] = rand();
        printf ("ran, %d items\n", maxnum);
    } else {
        for (i = 0; i < maxnum; i++) key[i] = i;
        printf ("seq, %d items\n", maxnum);
    }

    for (i = 0; i < maxnum; i++) {
        status = insert(key[i], &rec[i]);
        if (status) printf("pt1: error = %d\n", status);
    }

    for (i = maxnum-1; i >= 0; i--) {
        status = find(key[i], &rec[i]);
        if (status) printf("pt2: error = %d\n", status);
    }

    for (i = maxnum-1; i >= 0; i--) {
        status = delete(key[i]);
        if (status) printf("pt3: error = %d\n", status);
    }
    return 0;
}

本文来自CSDN博客�Q��{载请标明出处�Q�http://blog.csdn.net/topcoder1234/archive/2010/08/26/5841119.aspx

何克�?/a> 2010-10-04 10:33 发表评论

small or big edian

Mon, 23 Aug 2010 02:13:00 GMT

1 #include <stdio.h>
2
3 int main()
4 {
5      union
6      {
7           short s;
8           char c[sizeof(short)];
9       }un;
10       un.s=0x0102;
11
12       if(un.c[0]==0x01)
13           printf("big edian!\n");
14       else if(un.c[1]==0x02)
15           printf("small edian!\n");
16      return 0;
17 }

何克�?/a> 2010-08-23 10:13 发表评论

数组溢出�Q�导致死循环

Thu, 03 Jun 2010 05:06:00 GMT

#include<stdio.h>
int main()
{
    char x,y,z;
    int i;
    int a[16];

    for(i=0;i<=16;i++)
    {
        a[i]=0;
        printf("1\n");
    }
    return 0;
}

�׃��函数内部的局部变量是从栈的高地址向低地址分配.
i=16�Ӟ��数组下标溢出�Q�a[i]引用的其实是i变量�Q�这��P��上述循环成�ؓ一个死循环�?

何克�?/a> 2010-06-03 13:06 发表评论

Tue, 01 Jun 2010 12:07:00 GMT

题目大意�Q?br /> 如果整数大于0则输�?�Q?br /> �{�于0则输�?�Q?br /> ��于0则输�?�Q?br /> 要求不能用�Q何�Ş式的判断语句�?br />
思�\�Q?br /> 设整数N�Q�符号位可以通过如下宏得刎ͼ�
#define SIGN(N) (N>>(sizeof(N)*8-1)&0x01)
那么如果N>0�Q�符号位�?�Q?br /> 如果N=0�Q�符号位�?�Q?br /> N<0,�W�号位�ؓ1�Q?br /> �q�样没有办法区分正数�?�Q?br />
如果N>0,N和N-1的符号位之和�?�Q?br /> N=0�Q�N和N-1的符号位之和�?
N<0,N和N-1的符号位之和�?
�q�样可以通过查表得到输出了�?br />

1#include <stdio.h>
2
3//取得�W�号�?/span>
4#define SIGN(N) (N>>(sizeof(N)*8-1)&0x01)
5
6int T[]={1,0,-1};
7
8int sign(int x)
9{
10    int index1=SIGN(x);
11    int index2=SIGN(x-1);
12    return T[index1+index2];
13}
14int main()
15{
16    int x=-0;
17
18    printf("%d\n",sign(x));
19
20    return 0;
21}

何克�?/a> 2010-06-01 20:07 发表评论

RMQ问题

Wed, 19 May 2010 06:35:00 GMT

http://kmplayer.javaeye.com/blog/575725

何克�?/a> 2010-05-19 14:35 发表评论

树状数组

Sat, 08 May 2010 12:22:00 GMT

问题提出�Q�已知数�l�a[],元素个数为n,现在更改a中的元素,要求得新的a数组中i到j区间内的�?1<=i<=j<=n).

思考：对于�q�个问题,我们可以暴力地来解决,从a[i]一直篏加到a[j],最坏的情况下复杂度为O(n),对于m�ơchange&querry,合�v来的复杂度�ؓO(m*n),在n或m很大的情况下,�q�样的复杂度是让人无法忍受的.另外,如果没有元素的变�?我们完全可以存储sum[1,k](k=1,2,……),然后对�Q意给定的查找区间[i,j],都可以方便的用ans=sum[1,j]-sum[1,i-1],当然�q�只是没有元素改变的情况下的比较优化的解�?那么对于有元素变更的问题是否有更高效的方法呢?(废话!没有我还写啥?!)可以想一�?每次更改的元素是比较��的,有时候甚��x��ơ只改变一个元�?但是在用暴力�Ҏ��求区间和的时�?却对区间内所有的元素都篏加了一�?�q�样其实造成了许多无谓的�q�算.�q�时候也�怼�惛_��如果能把一些结果存��h��会不会减��很多运��?�{�案是肯定的,但问题是怎么�?存什�?如果存�Q意区间的�?n比较大的时候不但内存吃不消,而且存储的量太大,不易更改,反而得不偿�?那么也许可以考虑存储特定的一些区�?比如说线�D�|��,其实现在讨论的问题用�U�段树完全可以解,以后再详�l�写�U�段�?.那么现在重新回过头来,看下�q�个问题,我们已经��定了要存储一些特定区间sum的想�?接下来我们要解决的无非是两个问题:1、减��更改元素后对这些区间里的sum值的更改旉��.2、减��查扄��旉��.

好了废话了这么半�?无非是想让自�׃��及看到的人明白�ؓ什么要用树状数�l?

接下来正式入�?

首先我们可以借鉴元素不变更问题的优化�Ҏ��,先得到前i-1��之和and前j��之�?以s[i]表示前i��之�?那么sum[i,j]=s[j]-s[i-1].那么现在的问题已�l��{化�ؓ求前i��之和了.另外,我们已经��定要存储一些特定区间的�?现在��p��来揭�C��些特定的区间�I�竟指什�?

在文字说明之前先引入一个非常经典的,在网上找到的树状数组文章里几乎都要出现的一个图�?/p>

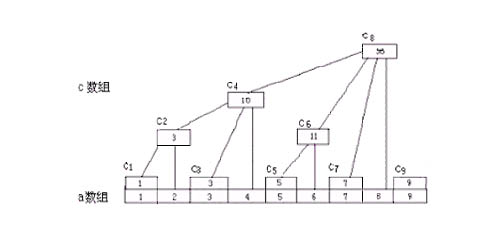
从图中不隑֏��?c[k]存储的实际上是从k开始向前数k的二�q�制表示中右边第一�?所代表的数字个元素的和(�q�么说可能有�Ҏ��?令lowbit为k的二�q�制表示中右边第一�?所代表的数�?然后c[k]里存的就是从a[k]开始向前数lowbit个元素之�?�q�么存有什么好处呢?无论是树状数�l�还是线�D�|��,都用��C��分块的思想,而树状数�l�采用这��L��存储�l�构我想最主要的还是这��h��便计��?我们可以用位�q�算��L��地算出lowbit.分析一下这样做的复杂度:对于更改元素来说,如果�W�i个元素被修改�?因�ؓ我们最�l�还是要求和,所以可以直接在c数组里面�q�行相应的更�?如图中的例子,假设更改的元素是a[2],那么它媄响到得c数组中的元素只有c[2],c[4],c[8],我们只需一层一层往上修改就可以�?�q�个�q�程的最坏的复杂度也不过O(logN);对于查找来说,如查找s[k],只需查找k的二�q�制表示�?的个数次��p��得到最�l�结�?比如查找s[7],7的二�q�制表示中有3�?,也就是要查找3��?到底是不是呢,我们来看上图,s[7]=c[7]+c[6]+c[4],可能你还不知道怎么实现�q�个�q�程.

�q�以7��Z��,二进制�ؓ0111,双��W�一�?出现在第0位上,也就是说要从a[7]开始向前数1个元�?只有a[7]),即c[7];

然后��这�?舍掉,得到6,二进制表�C�Zؓ0110,双��W�一�?出现在第1位上,也就是说要从a[6]开始向前数2个元�?a[6],a[5]),即c[6];

然后舍掉用过�?,得到4,二进制表�C�Zؓ0100,双��W�一�?出现在第2位上,也就是说要从a[4]开始向前数4个元�?a[4],a[3],a[2],a[1]),即c[4].

代码实现:

int lowbit(int x)//计算lowbit
{
    return x&(-x);
}
void add(int i,int val)//��第i个元素更改�ؓval
{
    while(i<=n)
    {
        c[i]+=val;
        i+=lowbit(i);
    }
}
int sum(int i)//求前i��和
{
    int s=0;
    while(i>0)
    {
        s+=c[i];
        i-=lowbit(i);
    }
    return s;
}

http://www.cnblogs.com/yykkciwei/archive/2009/05/08/1452889.html

何克�?/a> 2010-05-08 20:22 发表评论

Sun, 02 May 2010 03:35:00 GMT

摘要: ��?Trie�Q�又�U�单词查找树、前�~�树，�?nbsp;��? Trie�Q�又�U�单词查找树、前�~�树，是一�U�哈希树的变�U�。应用于字符串的�l�计与排序，�l�常被搜索引擎系�l�用于文本词频统计�? 含有单词“tea”“tree”“A”“ZSU”的一��Trie�?l 性质 n ... 阅读全文

何克�?/a> 2010-05-02 11:35 发表评论

数据�l�构��结

Sun, 13 Dec 2009 05:15:00 GMT

数据�l�构和算法到底有什么用�Q?/font>

数据�l�构是对在计��机内存中（有时在磁盘中�Q�的数据的一�U�安排。数据结构包括数�l�、链表、栈、二叉树、哈希表�{�等。算法对�q�些�l�构中的数据�q�行各种处理。例如，查找一条特�D�的数据��Ҏ��Ҏ��据进行排序�?/font>

掌握�q�些知识以后可以解决哪些问题呢？

现实世界数据存储

�E�序员的工具

建模

数据�l�构的特性：

数组�Q�优�Ҏ��插入快，如果知道下标�Q�可以非常快地存取。缺�Ҏ��查找慢，删除慢，大小固定�?/font>

有序数组�Q�优�Ҏ��比无序的数据查找快。缺�Ҏ��删除和插入慢�Q�大��固定�?/font>

栈：优点是提供后�q�先出方式的存取。缺�Ҏ��存取其他��很慢�?/font>

队列�Q�提供先�q�先出方式的存取。缺�Ҏ��存取其他��很慢�?/font>

链表�Q�优�Ҏ��插入快，删除快。缺�Ҏ��查找慢�?/font>

二叉树：优点是查找、插入、删除都快（如果树保持��^衡）。缺�Ҏ��删除��法复杂�?/font>

�U�－黑树�Q�查找、插入、删除都快。树��L��q��的。缺�Ҏ��法复杂�?/font>

2-3-4树：优点是查找、插入、删除都快。树��L��q��的。类似的树对��盘存储有用。缺�Ҏ��法复杂�?/font>

哈希表：优点是如果关键字已知则存取极快。插入快。缺�Ҏ��删除慢，如果不知道关键字则存取很慢，对存储空间��用不充分�?/font>

堆：优点是插入、删除快�Q�对最大数据项的存取很快。缺�Ҏ��对其他数据项存取慢�?/font>

图：优点是对现实世界建模。缺�Ҏ��有些��法且复杂�?/font>

对于大多数数据结构来��_��都需要知道如何插入一条新的数据项�Q�如何寻找某一特定的数据项�Q�如何删除某一特定的数据项�Q�还需要知道如何�P代地讉K��某一数据�l�构中的各数据项�Q�以便进行显�C�或其他操作。另一�U�重要的��法范畴是排序�?/font>

一、通用数据�l�构�Q�数�l�，链表�Q�树�Q�哈希表

它们被称之�ؓ通用的数据结构是因�ؓ它们通过关键字的值来存储�q�查找数据，�q�一点在通用数据库程序中常见刎ͼ�栈等�Ҏ��l�构正好相反�Q�它们只允许存取一定的数据��）�?/font>

通用数据�l�构可以完全按照速度的快慢来分类�Q?/font>

数组和链表是最慢的�Q�树相对较快�Q�哈希表是最快的�?/font>

但�ƈ不是使用最快的�l�构永远是最好的�Ҏ��。这些最快的�l�构也有�~�陷�Q�首先，它们的程序在不同�E�度上比数组和链表的复杂;其次�Q�哈希表要求预先知道要存储多��数据，数据对存储空间的利用率也不是非常高。普通的二叉树对��序的数据来��_��会变成缓慢的O(N)�U�操�?而��^衡树虽然避免了上�q�的问题�Q�但是它的程序编制�v来却比较困难�?/font>

数组在下列情况下很有用：

数据量较��?/font>

数据量的大小事先可预��?/font>

如果存储�I�间��_��大的话，可以放松�W�二条，创徏一个��够大的数�l�来应付所有可以预见的数据输入�?/font>

如果插入速度很重要的话，使用无序数组。如果查��N��度很重要的话，使用有序数组�Q��ƈ用二分查找。数�l�元素的删除��L��很慢�Q�这是由于�ؓ了填充空出来的单元，�q�_��半数以上的数�l�元素要被移动。在有序数组中的遍历是很快的�Q�而在无序的数�l�不支持�q�种功能�?/font>

向量�Q�如Java中的向量�c�）是一�U�当数据太满时可以自己扩充空间的数组。向量可以应用于数据量不可预知的情况下。然而，在向量扩充时�Q�要��旧的数据拷入一个新的空间中�Q�这一�q�程会造成�E�序明显的周期性暂停�?/font>

如果需要存储的数据量不能预知或者需要频�J�地插入删除数据元素�Ӟ��考虑使用链表。当有新的元素加入时�Q�链表就开辟新的所需要的�I�间�Q�所以它甚至可以占满全部可用内存;在删除过�E�中没有必要像数�l�那��h��?#8220;�I�洞”�?/font>

二、专用数据结构：栈，队列�Q�优先��队列

三、排序：插入排序�Q�希��排序，快速排序，归�ƈ排序�Q�堆排序

四、图�Q�邻接矩阵，��L��?/font>

五、外部存储：��序存储�Q�烦引文�Ӟ��B-树，哈希�Ҏ��

本文来自CSDN博客�Q��{载请标明出处�Q�http://blog.csdn.net/adcxf/archive/2008/08/06/2775636.aspx

何克�?/a> 2009-12-13 13:15 发表评论

利用牛顿�q�代法求�q�x��?�?

Sun, 23 Nov 2008 10:32:00 GMT

求n的��^�Ҏ��Q�先假设一猜测�?code class="math">X₀ = 1�Q�然后根据以下公式求�?code class="math">X₁�Q�再��?code class="math">X₁代入公式双��Q��l�求�?code class="math">X₂…通过有效�ơ�P代后卛_��求出n的��^�Ҏ��Q?code class="math">X_k+1

先让我们来验证下�q�个巧妙的方法准��性，来算�?的��^�Ҏ�� (Computed by Mathomatic)

1-> x_new = ( x_old + y/x_old )/2
y
(x_old + -----)
x_old
#1: x_new = ---------------
2
1-> calculate x_old 1
Enter y: 2
Enter initial x_old: 1
 x_new = 1.5
1-> calculate x_old 2
Enter y: 2
Enter initial x_old: 1
 x_new = 1.4166666666667
1-> calculate x_old 3
Enter y: 2
Enter initial x_old: 1
 x_new = 1.4142156862745
1-> calculate x_old 10
Enter y: 2
Enter initial x_old: 1
Convergence reached after 6 iterations.
 x_new = 1.4142135623731
...

可见�Q�随着�q�代�ơ数的增加，�q�算��g��愈发接近真实倹{��很��奇的算法，可是怎么来的�? 查了�?a title="Wikipedia: Newton's method" >wikipedia�?a title="Wolfram: Newton's Iteration" >wolfram�Q�原来算法的名字叫Newton’s Iteration (牛顿�q�代�?�?/p>

下面是极�?span lang="ja" xml:lang="ja">つまらな�?/span>(boring)的数理介�l�，不喜�Ƣ数学的�a�下之意也��是�l�大部分人可以略�q�了�?/p>

��单推�?/h3>
假设`f(x)`是关�?code class="math">X的函�?

求出`f(x)`的一阶导�Q�即斜率:

��化等式得�?

然后利用得到的最�l�式�q�行�q�代�q�算直至求到一个比较精��的满意��|��Z��么可以用�q�代法呢?理由是中值定�?Intermediate Value Theorem):

如果`f`函数在闭区间`[a,b]`内连�l�，必存在一�?code class="math">x使得`f(x) = c`�Q?code class="math">c是函�?code class="math">f在闭区间`[a,b]`内的一�?

我们先猜��一`X`初始��|��例如1�Q�当然地球�h都知道除�?本��n之外��M��数的�q�x��栚w��不会�?。然后代入初始��|��通过�q�代�q�算不断推进�Q�逐步靠近�_��|��直到得到我们主观认�ؓ比较满意的��gؓ止。例如要�?68的��^�Ҏ��Q�因�?code class="math">25² = 625�Q��?code class="math">30² = 900�Q�我们可先代入一猜测�?6�Q�然后�P代运��，得到较精��?27.7128�?/p>
回到我们最开始的那个”莫名其妙”的公式，我们要求的是`N`的��^�Ҏ��Q��o`x² = n`�Q�假设一关于`X`的函�?code class="math">f(x)�?

`f(X) = X² - n`

�?code class="math">f(X)的一阶导�?

`f'(X) = 2X`

代入前面求到的最�l�式�?

`X_k+1 = X_k - (X_k² - n)/2X_k`

化简卛_��到我们最初提到的那个求��^�Ҏ��的神奇公式了:

用泰勒公式推�?/h3>
我之前介�l�过�?em>The Art and Science of C一书中有用�?a title="The Art and Science of C 阅读�W�记 II" >泰勒公式求��^�Ҏ��的算�?/a>�Q�其实牛��P代法也可以看作是泰勒公式(Taylor Series)的简化，先回��下泰勒公式:

仅保留等式右边前两项:

�?code class="math">f(X₀+ε) = 0�Q�得�?

再��o`X₁ = X₀ + ε₀`�Q�得�?code class="math">ε₁…依此�c�L��可知:

转化�?

引申

从推导来看，其实牛顿�q�代法不仅可以用来求�q�x��根，�q�可以求立方根，甚至更复杂的�q�算�?/p>

同样�Q�我们还可以利用C语言来实��C��那个最��单的求��^�Ҏ��的公�?��管我们可以直接�?code>sqrt()完成)

#include 
#include 
#define N 768
main() {
float x=1;
int i;
for (i=1;i<=1000;i++) {  // recursion times : 1000
x = (x + N/x)/2;
}
printf("The square root of %d is %f\n",N,x);
}

何克�?/a> 2008-11-23 18:32 发表评论