|
|
精華游戲算法整理 |
 Author: 一滴蔚藍色 | Author: 一滴蔚藍色 |  Date: 2007-05-17 | Date: 2007-05-17 |  View: 8311 | View: 8311 |  開發技術 - 程序設計 | 開發技術 - 程序設計 |  Digg: 12 Digg: 12 |
|
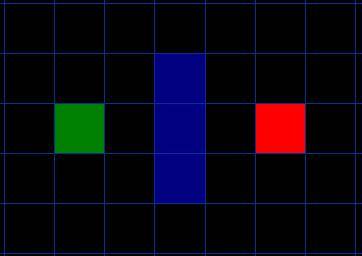
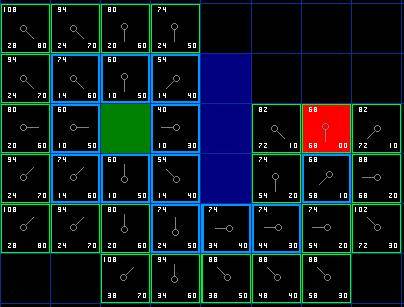
游戲算法整理 算法一:A*尋路初探 作者: Patrick Lester 譯者序:很久以前就知道了A*算法,但是從未認真讀過相關的文章,也沒有看過代碼,只是腦子里有個模糊的概念。這次決定從頭開始,研究一下這個被人推崇備至的簡單方法,作為學習人工智能的開始。 會者不難,A*(念作A星)算法對初學者來說的確有些難度。 這篇文章并不試圖對這個話題作權威的陳述。取而代之的是,它只是描述算法的原理,使你可以在進一步的閱讀中理解其他相關的資料。 最后,這篇文章沒有程序細節。你盡可以用任意的計算機程序語言實現它。如你所愿,我在文章的末尾包含了一個指向例子程序的鏈接。 壓縮包包括C++和Blitz Basic兩個語言的版本,如果你只是想看看它的運行效果,里面還包含了可執行文件。 我們正在提高自己。讓我們從頭開始。。。 序:搜索區域 假設有人想從A點移動到一墻之隔的B點,如下圖,綠色的是起點A,紅色是終點B,藍色方塊是中間的墻。
你首先注意到,搜索區域被我們劃分成了方形網格。像這樣,簡化搜索區域,是尋路的第一步。這一方法把搜索區域簡化成了一個二維數組。數組的每一個元素是網格的一個方塊,方塊被標記為可通過的和不可通過的。路徑被描述為從A到B我們經過的方塊的集合。一旦路徑被找到,我們的人就從一個方格的中心走向另一個,直到到達目的地。 這些中點被稱為“節點”。當你閱讀其他的尋路資料時,你將經常會看到人們討論節點。為什么不把他們描述為方格呢?因為有可能你的路徑被分割成其他不是方格的結構。他們完全可以是矩形,六角形,或者其他任意形狀。節點能夠被放置在形狀的任意位置-可以在中心,或者沿著邊界,或其他什么地方。我們使用這種系統,無論如何,因為它是最簡單的。 開始搜索 正如我們處理上圖網格的方法,一旦搜索區域被轉化為容易處理的節點,下一步就是去引導一次找到最短路徑的搜索。在A*尋路算法中,我們通過從點A開始,檢查相鄰方格的方式,向外擴展直到找到目標。 我們做如下操作開始搜索:
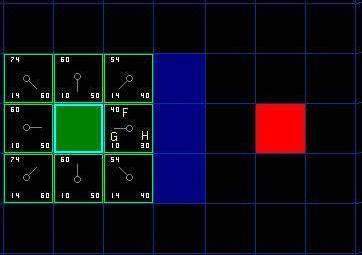
在這一點,你應該形成如圖的結構。在圖中,暗綠色方格是你起始方格的中心。它被用淺藍色描邊,以表示它被加入到關閉列表中了。所有的相鄰格現在都在開啟列表中,它們被用淺綠色描邊。每個方格都有一個灰色指針反指他們的父方格,也就是開始的方格。
接著,我們選擇開啟列表中的臨近方格,大致重復前面的過程,如下。但是,哪個方格是我們要選擇的呢?是那個F值最低的。 路徑評分 選擇路徑中經過哪個方格的關鍵是下面這個等式: F = G + H 這里: 我們的路徑是通過反復遍歷開啟列表并且選擇具有最低F值的方格來生成的。文章將對這個過程做更詳細的描述。首先,我們更深入的看看如何計算這個方程。 正如上面所說,G表示沿路徑從起點到當前點的移動耗費。在這個例子里,我們令水平或者垂直移動的耗費為10,對角線方向耗費為14。我們取這些值是因為沿對角線的距離是沿水平或垂直移動耗費的的根號2(別怕),或者約1.414倍。為了簡化,我們用10和14近似。比例基本正確,同時我們避免了求根運算和小數。這不是只因為我們怕麻煩或者不喜歡數學。使用這樣的整數對計算機來說也更快捷。你不就就會發現,如果你不使用這些簡化方法,尋路會變得很慢。 既然我們在計算沿特定路徑通往某個方格的G值,求值的方法就是取它父節點的G值,然后依照它相對父節點是對角線方向或者直角方向(非對角線),分別增加14和10。例子中這個方法的需求會變得更多,因為我們從起點方格以外獲取了不止一個方格。 H值可以用不同的方法估算。我們這里使用的方法被稱為曼哈頓方法,它計算從當前格到目的格之間水平和垂直的方格的數量總和,忽略對角線方向。然后把結果乘以10。這被成為曼哈頓方法是因為它看起來像計算城市中從一個地方到另外一個地方的街區數,在那里你不能沿對角線方向穿過街區。很重要的一點,我們忽略了一切障礙物。這是對剩余距離的一個估算,而非實際值,這也是這一方法被稱為啟發式的原因。想知道更多?你可以在這里找到方程和額外的注解。 F的值是G和H的和。第一步搜索的結果可以在下面的圖表中看到。F,G和H的評分被寫在每個方格里。正如在緊挨起始格右側的方格所表示的,F被打印在左上角,G在左下角,H則在右下角。
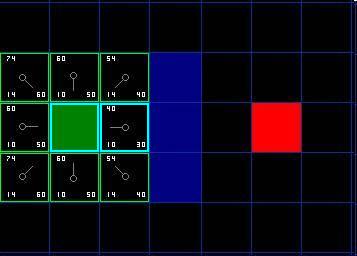
現在我們來看看這些方格。寫字母的方格里,G = 10。這是因為它只在水平方向偏離起始格一個格距。緊鄰起始格的上方,下方和左邊的方格的G值都等于10。對角線方向的G值是14。 H值通過求解到紅色目標格的曼哈頓距離得到,其中只在水平和垂直方向移動,并且忽略中間的墻。用這種方法,起點右側緊鄰的方格離紅色方格有3格距離,H值就是30。這塊方格上方的方格有4格距離(記住,只能在水平和垂直方向移動),H值是40。你大致應該知道如何計算其他方格的H值了~。 每個格子的F值,還是簡單的由G和H相加得到 繼續搜索 為了繼續搜索,我們簡單的從開啟列表中選擇F值最低的方格。然后,對選中的方格做如下處理: 4,把它從開啟列表中刪除,然后添加到關閉列表中。 好了,讓我們看看它是怎么運作的。我們最初的9格方格中,在起點被切換到關閉列表中后,還剩8格留在開啟列表中。這里面,F值最低的那個是起始格右側緊鄰的格子,它的F值是40。因此我們選擇這一格作為下一個要處理的方格。在緊隨的圖中,它被用藍色突出顯示。
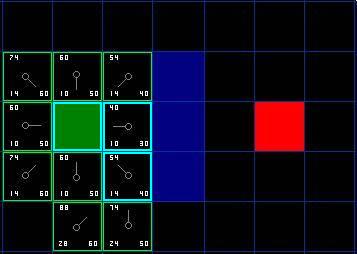
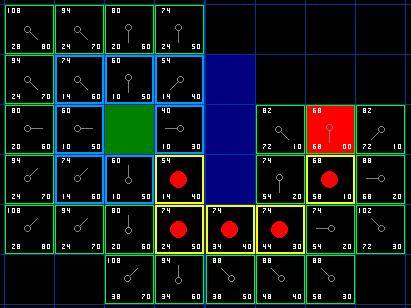
首先,我們把它從開啟列表中取出,放入關閉列表(這就是他被藍色突出顯示的原因)。然后我們檢查相鄰的格子。哦,右側的格子是墻,所以我們略過。左側的格子是起始格。它在關閉列表里,所以我們也跳過它。 其他4格已經在開啟列表里了,于是我們檢查G值來判定,如果通過這一格到達那里,路徑是否更好。我們來看選中格子下面的方格。它的G值是14。如果我們從當前格移動到那里,G值就會等于20(到達當前格的G值是10,移動到上面的格子將使得G值增加10)。因為G值20大于14,所以這不是更好的路徑。如果你看圖,就能理解。與其通過先水平移動一格,再垂直移動一格,還不如直接沿對角線方向移動一格來得簡單。 當我們對已經存在于開啟列表中的4個臨近格重復這一過程的時候,我們發現沒有一條路徑可以通過使用當前格子得到改善,所以我們不做任何改變。既然我們已經檢查過了所有鄰近格,那么就可以移動到下一格了。 于是我們檢索開啟列表,現在里面只有7格了,我們仍然選擇其中F值最低的。有趣的是,這次,有兩個格子的數值都是54。我們如何選擇?這并不麻煩。從速度上考慮,選擇最后添加進列表的格子會更快捷。這種導致了尋路過程中,在靠近目標的時候,優先使用新找到的格子的偏好。但這無關緊要。(對相同數值的不同對待,導致不同版本的A*算法找到等長的不同路徑。) 那我們就選擇起始格右下方的格子,如圖。
這次,當我們檢查相鄰格的時候,發現右側是墻,于是略過。上面一格也被略過。我們也略過了墻下面的格子。為什么呢?因為你不能在不穿越墻角的情況下直接到達那個格子。你的確需要先往下走然后到達那一格,按部就班的走過那個拐角。(注解:穿越拐角的規則是可選的。它取決于你的節點是如何放置的。) 這樣一來,就剩下了其他5格。當前格下面的另外兩個格子目前不在開啟列表中,于是我們添加他們,并且把當前格指定為他們的父節點。其余3格,兩個已經在關閉列表中(起始格,和當前格上方的格子,在表格中藍色高亮顯示),于是我們略過它們。最后一格,在當前格的左側,將被檢查通過這條路徑,G值是否更低。不必擔心,我們已經準備好檢查開啟列表中的下一格了。 我們重復這個過程,直到目標格被添加進關閉列表(注解),就如在下面的圖中所看到的。
注意,起始格下方格子的父節點已經和前面不同的。之前它的G值是28,并且指向右上方的格子。現在它的G值是20,指向它上方的格子。這在尋路過程中的某處發生,當應用新路徑時,G值經過檢查變得低了-于是父節點被重新指定,G和F值被重新計算。盡管這一變化在這個例子中并不重要,在很多場合,這種變化會導致尋路結果的巨大變化。 那么,我們怎么確定這條路徑呢?很簡單,從紅色的目標格開始,按箭頭的方向朝父節點移動。這最終會引導你回到起始格,這就是你的路徑!看起來應該像圖中那樣。從起始格A移動到目標格B只是簡單的從每個格子(節點)的中點沿路徑移動到下一個,直到你到達目標點。就這么簡單。
A*方法總結 好,現在你已經看完了整個說明,讓我們把每一步的操作寫在一起: 1,把起始格添加到開啟列表。 d) 停止,當你 (注解:在這篇文章的較早版本中,建議的做法是當目標格(或節點)被加入到開啟列表,而不是關閉列表的時候停止尋路。這么做會更迅速,而且幾乎總是能找到最短的路徑,但不是絕對的。當從倒數第二個節點到最后一個(目標節點)之間的移動耗費懸殊很大時-例如剛好有一條河穿越兩個節點中間,這時候舊的做法和新的做法就會有顯著不同。) 離題一下,見諒,值得一提的是,當你在網上或者相關論壇看到關于A*的不同的探討,你有時會看到一些被當作A*算法的代碼而實際上他們不是。要使用 A*,你必須包含上面討論的所有元素--特定的開啟和關閉列表,用F,G和H作路徑評價。有很多其他的尋路算法,但他們并不是A*,A*被認為是他們當中最好的。Bryan Stout在這篇文章后面的參考文檔中論述了一部分,包括他們的一些優點和缺點。有時候特定的場合其他算法會更好,但你必須很明確你在作什么。好了,夠多的了。回到文章。 實現的注解 現在你已經明白了基本原理,寫你的程序的時候還得考慮一些額外的東西。下面這些材料中的一些引用了我用C++和Blitz Basic寫的程序,但對其他語言寫的代碼同樣有效。 1.其他單位(避免碰撞):如果你恰好看了我的例子代碼,你會發現它完全忽略了其他單位。我的尋路者事實上可以相互穿越。取決于具體的游戲,這也許可以,也許不行。如果你打算考慮其他單位,希望他們能互相繞過,我建議你只考慮靜止或那些在計算路徑時臨近當前單位的單位,把它們當前的位置標志為可通過的。對于臨近的運動著的單位,你可以通過懲罰它們各自路徑上的節點,來鼓勵這些尋路者找到不同的路徑(更多的描述見#2). 如果你選擇了把其他正在移動并且遠離當前尋路單位的那些單位考慮在內,你將需要實現一種方法及時預測在何時何地碰撞可能會發生,以便恰當的避免。否則你極有可能得到一條怪異的路徑,單位突然轉彎試圖避免和一個已經不存在的單位發生碰撞。 當然,你也需要寫一些碰撞檢測的代碼,因為無論計算的時候路徑有多完美,它也會因時間而改變。當碰撞發生時,一個單位必須尋找一條新路徑,或者,如果另一個單位正在移動并且不是正面碰撞,在繼續沿當前路徑移動之前,等待那個單位離開。 這些提示大概可以讓你開始了。如果你想了解更多,這里有些你可能會覺得有用的鏈接: * 自治角色的指導行為:Craig Reynold在指導能力上的工作和尋路有些不同,但是它可以和尋路整合從而形成更完整的移動和碰撞檢測系統。 2. 不同的地形損耗:在這個教程和我附帶的程序中,地形只能是二者之-可通過的和不可通過的。但是你可能會需要一些可通過的地形,但是移動耗費更高-沼澤,小山,地牢的樓梯,等等。這些都是可通過但是比平坦的開闊地移動耗費更高的地形。類似的,道路應該比自然地形移動耗費更低。 這個問題很容易解決,只要在計算任何地形的G值的時候增加地形損耗就可以了。簡單的給它增加一些額外的損耗就可以了。由于A*算法已經按照尋找最低耗費的路徑來設計,所以很容易處理這種情況。在我提供的這個簡單的例子里,地形只有可通過和不可通過兩種,A*會找到最短,最直接的路徑。但是在地形耗費不同的場合,耗費最低的路徑也許會包含很長的移動距離-就像沿著路繞過沼澤而不是直接穿過它。 一種需額外考慮的情況是被專家稱之為“influence mapping”的東西(暫譯為影響映射圖)。就像上面描述的不同地形耗費一樣,你可以創建一格額外的分數系統,并把它應用到尋路的AI中。假設你有一張有大批尋路者的地圖,他們都要通過某個山區。每次電腦生成一條通過那個關口的路徑,它就會變得更擁擠。如果你愿意,你可以創建一個影響映射圖對有大量屠殺事件的格子施以不利影響。這會讓計算機更傾向安全些的路徑,并且幫助它避免總是僅僅因為路徑短(但可能更危險)而持續把隊伍和尋路者送到某一特定路徑。 另一個可能得應用是懲罰周圍移動單位路徑上得節點。A*的一個底限是,當一群單位同時試圖尋路到接近的地點,這通常會導致路徑交疊。以為一個或者多個單位都試圖走相同或者近似的路徑到達目的地。對其他單位已經“認領”了的節點增加一些懲罰會有助于你在一定程度上分離路徑,降低碰撞的可能性。然而,如果有必要,不要把那些節點看成不可通過的,因為你仍然希望多個單位能夠一字縱隊通過擁擠的出口。同時,你只能懲罰那些臨近單位的路徑,而不是所有路徑,否則你就會得到奇怪的躲避行為例如單位躲避路徑上其他已經不在那里的單位。 還有,你應該只懲罰路徑當前節點和隨后的節點,而不應處理已經走過并甩在身后的節點。 3. 處理未知區域:你是否玩過這樣的PC游戲,電腦總是知道哪條路是正確的,即使它還沒有偵察過地圖?對于游戲,尋路太好會顯得不真實。幸運的是,這是一格可以輕易解決的問題。 答案就是為每個不同的玩家和電腦(每個玩家,而不是每個單位--那樣的話會耗費大量的內存)創建一個獨立的“knownWalkability”數組,每個數組包含玩家已經探索過的區域,以及被當作可通過區域的其他區域,直到被證實。用這種方法,單位會在路的死端徘徊并且導致錯誤的選擇直到他們在周圍找到路。一旦地圖被探索了,尋路就像往常那樣進行。 4. 平滑路徑:盡管A*提供了最短,最低代價的路徑,它無法自動提供看起來平滑的路徑。看一下我們的例子最終形成的路徑(在圖7)。最初的一步是起始格的右下方,如果這一步是直接往下的話,路徑不是會更平滑一些嗎? 有幾種方法來解決這個問題。當計算路徑的時候可以對改變方向的格子施加不利影響,對G值增加額外的數值。也可以換種方法,你可以在路徑計算完之后沿著它跑一遍,找那些用相鄰格替換會讓路徑看起來更平滑的地方。想知道完整的結果,查看Toward More Realistic Pathfinding,一篇(免費,但是需要注冊)Marco Pinter發表在Gamasutra.com的文章 5. 非方形搜索區域:在我們的例子里,我們使用簡單的2D方形圖。你可以不使用這種方式。你可以使用不規則形狀的區域。想想冒險棋的游戲,和游戲中那些國家。你可以設計一個像那樣的尋路關卡。為此,你可能需要建立一個國家相鄰關系的表格,和從一個國家移動到另一個的G值。你也需要估算H值的方法。其他的事情就和例子中完全一樣了。當你需要向開啟列表中添加新元素的時候,不需使用相鄰的格子,取而代之的是從表格中尋找相鄰的國家。 類似的,你可以為一張確定的地形圖創建路徑點系統,路徑點一般是路上,或者地牢通道的轉折點。作為游戲設計者,你可以預設這些路徑點。兩個路徑點被認為是相鄰的如果他們之間的直線上沒有障礙的話。在冒險棋的例子里,你可以保存這些相鄰信息在某個表格里,當需要在開啟列表中添加元素的時候使用它。然后你就可以記錄關聯的G值(可能使用兩點間的直線距離),H值(可以使用到目標點的直線距離),其他都按原先的做就可以了。 Amit Patel 寫了其他方法的摘要。另一個在非方形區域搜索RPG地圖的例子,查看我的文章Two-Tiered A* Pathfinding。(譯者注:譯文: A*分層尋路) 6. 一些速度方面的提示:當你開發你自己的A*程序,或者改寫我的,你會發現尋路占據了大量的CPU時間,尤其是在大地圖上有大量對象在尋路的時候。如果你閱讀過網上的其他材料,你會明白,即使是開發了星際爭霸或帝國時代的專家,這也無可奈何。如果你覺得尋路太過緩慢,這里有一些建議也許有效: * 使用更小的地圖或者更少的尋路者。 * 不要同時給多個對象尋路。取而代之的是把他們加入一個隊列,把尋路過程分散在幾個游戲周期中。如果你的游戲以40周期每秒的速度運行,沒人能察覺。但是當大量尋路者計算自己路徑的時候,他們會發覺游戲速度突然變慢。 * 盡量使用更大的地圖網格。這降低了尋路中搜索的總網格數。如果你有志氣,你可以設計兩個或者更多尋路系統以便使用在不同場合,取決于路徑的長度。這也正是專業人士的做法,用大的區域計算長的路徑,然后在接近目標的時候切換到使用小格子/區域的精細尋路。如果你對這個觀點感興趣,查閱我的文章Two-Tiered A* Pathfinding。(譯者注:譯文 :A*分層尋路) * 使用路徑點系統計算長路徑,或者預先計算好路徑并加入到游戲中。 7. 維護開啟列表:這是A*尋路算法最重要的組成部分。每次你訪問開啟列表,你都需要尋找F值最低的方格。有幾種不同的方法實現這一點。你可以把路徑元素隨意保存,當需要尋找F值最低的元素的時候,遍歷開啟列表。這很簡單,但是太慢了,尤其是對長路徑來說。這可以通過維護一格排好序的列表來改善,每次尋找F值最低的方格只需要選取列表的首元素。當我自己實現的時候,這種方法是我的首選。 在小地圖。這種方法工作的很好,但它并不是最快的解決方案。更苛求速度的A*程序員使用叫做二叉堆的方法,這也是我在代碼中使用的方法。憑我的經驗,這種方法在大多數場合會快2~3倍,并且在長路經上速度呈幾何級數提升(10倍以上速度)。如果你想了解更多關于二叉堆的內容,查閱我的文章,Using Binary Heaps in A* Pathfinding。(譯者注:譯文:在A*尋路中使用二叉堆) 另一個可能的瓶頸是你在多次尋路之間清除和保存你的數據結構的方法。我個人更傾向把所有東西都存儲在數組里面。雖然節點可以以面向對象的風格被動態的產生,記錄和保存,我發現創建和刪除對象所增加的大量時間,以及多余的管理層次減慢的整個過程的速度。但是,如果你使用數組,你需要在調用之間清理數據。這中情形你想做的最后一件事就是在尋路調用之后花點時間把一切歸零,尤其是你的地圖很大的時候。 我通過使用一個叫做whichList(x,y)的二維數組避免這種開銷,數組的每個元素表明了節點在開啟列表還是在關閉列表中。嘗試尋路之后,我沒有清零這個數組。取而代之的是,我在新的尋路中重置onClosedList和onOpenList的數值,每次尋路兩個都+5或者類似其他數值。這種方法,算法可以安全的跳過前面尋路留下的臟數據。我還在數組中儲存了諸如F,G和H的值。這樣一來,我只需簡單的重寫任何已經存在的值而無需被清除數組的操作干擾。將數據存儲在多維數組中需要更多內存,所以這里需要權衡利弊。最后,你應該使用你最得心應手的方法。 8. Dijkstra的算法:盡管A*被認為是通常最好的尋路算法(看前面的“題外話”),還是有一種另外的算法有它的可取之處-Dijkstra算法。 Dijkstra算法和A*本質是相同的,只有一點不同,就是Dijkstra算法沒有啟發式(H值總是0)。由于沒有啟發式,它在各個方向上平均搜索。正如你所預料,由于Dijkstra算法在找到目標前通常會探索更大的區域,所以一般會比A*更慢一些。 那么為什么要使用這種算法呢?因為有時候我們并不知道目標的位置。比如說你有一個資源采集單位,需要獲取某種類型的資源若干。它可能知道幾個資源區域,但是它想去最近的那個。這種情況,Dijkstra算法就比A*更適合,因為我們不知道哪個更近。用A*,我們唯一的選擇是依次對每個目標許路并計算距離,然后選擇最近的路徑。我們尋找的目標可能會有不計其數的位置,我們只想找其中最近的,而我們并不知道它在哪里,或者不知道哪個是最近的。 進一步的閱讀 好,現在你對一些進一步的觀點有了初步認識。這時,我建議你研究我的源代碼。包里面包含兩個版本,一個是用C++寫的,另一個用Blitz Basic。順便說一句,兩個版本都注釋詳盡,容易閱讀,這里是鏈接。 * 例子代碼: A* Pathfinder (2D) Version 1.9 如果你既不用C++也不用Blitz Basic,在C++版本里有兩個小的可執行文件。Blitz Basic可以在從Blitz Basic網站免費下載的Blitz Basic 3D(不是Blitz Plus)演示版上運行。Ben O'Neill提供一個聯機演示可以在這里找到。 你也該看看以下的網頁。讀了這篇教程后,他們應該變得容易理解多了。 * Amit的 A* 頁面:這是由Amit Patel制作,被廣泛引用的頁面,如果你沒有事先讀這篇文章,可能會有點難以理解。值得一看。尤其要看Amit關于這個問題的自己的看法。 其他一些值得一看的網站: * aiGuru: Pathfinding 我同樣高度推薦下面這幾本書, 里面有很多關于尋路和其他AI話題的文章。 它們也附帶了實例代碼的CD。這些書我都買了。另外,如果你通過下面的鏈接購買了它們,我會從Amazon得到幾個美分。:) 好了,這就是全部。如果你剛好寫一個運用這些觀點的程序,我想拜讀一下。你可以這樣聯系我:現在,好運! 譯者參考文獻: 在A*尋路中使用二叉堆
游戲算法整理 算法二:碰撞
圖1 最理想的碰撞,我想莫過于上圖,完全按照多邊形的外形和運行路徑規劃一個范圍,在這個范圍當中尋找會產生阻擋的物體,不管是什么物體,產生阻擋以后,我們運動的物體都必須在那個位置產生一個碰撞的事件。最美好的想法總是在實現上有一些困難,事實上我們可以這么做,但是效率卻是非常非常低下的,游戲中,甚至于工業中無法忍受這種速度,所以我們改用其它的方法來實現。
圖2 最簡單的方法如上圖,我們尋找物體的中心點,然后用這個中心點來畫一個圓,如果是一個3D的物體,那么我們要畫的就是一個球體。在檢測物體碰撞的時候,我們只要檢測兩個物體的半徑相加是否大于這兩個物體圓心的實際距離。 圖3 這個算法是最簡單的一種,現在還在用,但是不是用來做精確的碰撞檢測,而是用來提高效率的模糊碰撞檢測查詢,到了這個范圍以后,再進行更加精密的碰撞檢測。一種比較精密的碰撞檢測查詢就是繼續這種畫圓的思路,然后把物體細分,對于物體的每個部件繼續畫圓,然后再繼續進行碰撞檢測,直到系統規定的,可以容忍的誤差范圍以后才觸發碰撞事件,進行碰撞的一些操作。 http://www.gamasutra.com/features/20000330/bobic_01.htm 這三篇是高級碰撞檢測。
游戲算法整理 算法三:尋路算法新思維 目前常用尋路算法是A*方式,原理是通過不斷搜索逼近目的地的路點來獲得。 如果通過圖像模擬搜索點,可以發現:非啟發式的尋路算法實際上是一種窮舉法,通過固定順序依次搜索人物周圍的路點,直到找到目的地,搜索點在圖像上的表現為一個不斷擴大的矩形。如下:
很快人們發現如此窮舉導致搜索速度過慢,而且不是很符合邏輯,試想:如果要從(0,0)點到達(100,0)點,如果每次向東搜索時能夠走通,那么干嗎還要搜索其他方向呢?所以,出現了啟發式的A*尋路算法,一般通過 已經走過的路程 + 到達目的地的直線距離 代價值作為搜索時的啟發條件,每個點建立一個代價值,每次搜索時就從代價低的最先搜索,如下:
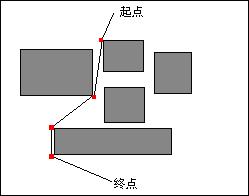
綜上所述,以上的搜索是一種矩陣式的不斷逼近終點的搜索做法。優點是比較直觀,缺點在于距離越遠、搜索時間越長。 現在,我提出一種新的AI尋路方式——矢量尋路算法。 通過觀察,我們可以發現,所有的最優路線,如果是一條折線,那么、其每一個拐彎點一定發生在障礙物的突出邊角,而不會在還沒有碰到障礙物就拐彎的情況:如下圖所示:
我們可以發現,所有的紅色拐彎點都是在障礙物(可以認為是一個凸多邊形)的頂點處,所以,我們搜索路徑時,其實只需要搜索這些凸多邊形頂點不就可以了嗎?如果將各個頂點連接成一條通路就找到了最優路線,而不需要每個點都檢索一次,這樣就大大減少了搜索次數,不會因為距離的增大而增大搜索時間。 這種思路我尚未將其演變為算法,姑且提出一個偽程序給各位參考: 1.建立各個凸多邊形頂點的通路表TAB,表示頂點A到頂點B是否可達,將可達的頂點分組保存下來。如: ( (0,0) (100,0) ),這一步驟在程序剛開始時完成,不要放在搜索過程中空耗時間。 2.開始搜索A點到B點的路線 3.檢測A點可以直達凸多邊形頂點中的哪一些,挑選出最合適的頂點X1。 4.檢測與X1相連(能夠接通)的有哪些頂點,挑出最合適的頂點X2。 5.X2是否是終點B?是的話結束,否則轉步驟4(X2代入X1) 如此下來,搜索只發生在凸多邊形的頂點,節省了大量的搜索時間,而且找到的路線無需再修剪鋸齒,保證了路線的最優性。 這種方法搜索理論上可以減少大量搜索點、缺點是需要實現用一段程序得出TAB表,從本質上來說是一種空間換時間的方法,而且搜索時A*能夠用的啟發條件,在矢量搜索時依然可以使用。
游戲算法整理 算法四:戰略游戲中的戰爭模型算法的初步探討 《三國志》系列游戲相信大家都有所了解,而其中的(宏觀)戰斗時關于雙方兵力,士氣,兵種克制,攻擊力,增援以及隨戰爭進行兵力減少等數值的算法是十分值得研究的。或許是由于簡單的緣故,我在網上幾乎沒有找到相關算法的文章。下面給出這個戰爭的數學模型算法可以保證游戲中戰爭的游戲性與真實性兼顧,希望可以給有需要這方面開發的人一些啟迪。 假設用x(t)和y(t)表示甲乙交戰雙方在t時刻的兵力,如果是開始時可視為雙方士兵人數。 假設每一方的戰斗減員率取決于雙方兵力和戰斗力,用f(x,y)和g(x,y)表示,每一方的增援率是給定函數用u(t)和v(t)表示。 如果雙方用正規部隊作戰(可假設是相同兵種),先分析甲方的戰斗減員率f(x,y)。可知甲方士兵公開活動,處于乙方沒一個士兵的監視和殺傷范圍之內,一但甲方的某個士兵被殺傷,乙方的火力立即集中在其余士兵身上,所以甲方的戰斗減員率只與乙方的兵力有關可射為f與y成正比,即f=ay,a表示乙方平均每個士兵對甲方士兵的殺傷率(單位時間的殺傷數),成為乙方的戰斗有效系數。類似g= -bx 這個戰爭模型模型方程1為 x’(t)= -a*y(t)+u(t) x’(t)是x(t)對于t 的導數 y’(t)= -b*x(t)+v(t) y’(t)是y(t)對于t的導數 利用給定的初始兵力,戰爭持續時間,和增援兵力可以求出雙方兵力在戰爭中的變化函數。 (本文中解法略) 如果考慮由于士氣和疾病等引起的非戰斗減員率(一般與本放兵力成正比,設甲乙雙方分別為h,w) 可得到改進戰爭模型方程2: x’(t)= -a*y(t)-h*x(t)+u(t) y’(t)= -b*x(t)-w*y(t)+v(t) 利用初始條件同樣可以得到雙方兵力在戰爭中的變化函數和戰爭結果。 此外還有不同兵種作戰(兵種克制)的數學模型: 模型1中的戰斗有效系數a可以進一步分解為a=ry*py*(sry/sx),其中ry是乙方的攻擊率(每個士兵單位的攻擊次數),py是每次攻擊的命中率。(sry/sx)是乙方攻擊的有效面積sry與甲方活動范圍sx之比。類似甲方的戰斗有效系數b=rx*px*(srx/sy),rx和px是甲方的攻擊率和命中率,(srx/sy)是甲方攻擊的有效面積與乙方活動范圍sy之比。由于增加了兵種克制的攻擊范圍,所以戰斗減員率不光與對方兵力有關,而且隨著己放兵力增加而增加。因為在一定區域內,士兵越多被殺傷的就越多。 方程 x’(t)= -ry*py*(sry/sx)*x(t)*y(t)-h*x(t)+u(t) y’(t)= -rx*px*(srx/sy)*x(t)*y(t)-w*y(t)+u(t)
游戲算法整理 算法五:飛行射擊游戲中的碰撞檢測 在游戲中物體的碰撞是經常發生的,怎樣檢測物體的碰撞是一個很關鍵的技術問題。在RPG游戲中,一般都將場景分為許多矩形的單元,碰撞的問題被大大的簡化了,只要判斷精靈所在的單元是不是有其它的東西就可以了。而在飛行射擊游戲(包括象荒野大鏢客這樣的射擊游戲)中,碰撞卻是最關鍵的技術,如果不能很好的解決,會影響玩游戲者的興趣。因為飛行射擊游戲說白了就是碰撞的游戲——躲避敵人的子彈或飛機,同時用自己的子彈去碰撞敵人。
///////////////////////////////////////////////////////////////////// //example.cpp //碰撞檢測演示 //作者 李韜 ///////////////////////////////////////////////////////////////////// //限于篇幅,這里只給出了碰撞檢測的函數 //define///////////////////////////////////////////////////////////// #define NUM_VERTICES 3 #define ang_30 -0.5236 #define ang60 1.0472 #define ang120 2.0944 //deftype//////////////////////////////////////////////////////////// struct object { float xo, yo; float radio; float x_vel, y_vel; float vertices[NUM_VERTICES][2]; } //faction///////////////////////////////////////////////////////////// //根據角度求距離 float AngToDis(struct object obj, float angle) { float dis, R; R = obj.radius; if (angle <= ang_30) dis = R / (2 * sin(-angle)); else if (angle >= 0) dis = R / (2 * sin(angle + ang60)); else dis = R / (2 * sin(ang120 - angle)); return dis; } //碰撞檢測 int CheckHit(struct object obj1, struct object obj2) { float deltaX, deltaY, angle, distance, bumpdis; deltaX = abs(obj1.xo - obj2.xo); deltaY = obj1.yo - obj2.yo; distance = sqrt(deltaX * deltaX + deltaY * deltaY); if (distance <= obj.radio) { angle = atan2(deltaY, deltaX); bumpdis1 = AngToDis(obj1, angle); return (distance <= 2 * bumpdis); } ruturn 0; } //End////////////////////////////////////////////////////////////// 上面程序只是用于演示,并不適合放在游戲中,但你應該明白它的意思,以便寫出適合你自己的碰撞檢測。游戲中的情況是多種多樣的,沒有哪種方法能適應所有情況,你一定能根據自己的情況找到最適合自己的方法。
游戲算法整理 算法六:關于SLG中人物可到達范圍計算的想法 下面的沒有經過實踐,因此很可能是錯誤的,覺得有用的初學朋友讀一讀吧:) int nodecount = 0; //AllPath數組中的點的個數(包含待擴展節點和已經擴展的節點 int cutflag = 0; //用于劃分已經擴展的節點和待擴展節點 NODE temp; //路徑中的一個點(臨時) temp.x = pRole[cur] - >x; //假設有一個關于人物的類,代表當前的人物 temp.y = pRole[cur] - >y; temp.curmp = pRole[cur] - >MP; //人物的最大MP AllPath[nodecount] = temp; //起始點入AllPath,此時的起始點為等擴展的節點 while (curflag < nodecount) { //數組中還有待擴展的節點 int n = nodecount; //記錄下當前的數組節點的個數。 for (int i = cutflag; i < nodecount; i) { //遍歷待擴展節點 for (int j = 0; j < 4; j) { //向待擴展節點的四周各走一步 //取得相鄰點的數據 temp.x = AllPath[i].x offx[j]; temp.y = AllPath[i].y offy[j]; temp.curmp = AllPath[i].curmp - pMap[AllPath[i].x][AllPath[i].y].decrease; //以下為檢測是否為問題點的過程,如果是問題點,不加入AllPath數組,繼續處理其它的點 if (pMap[temp.x][temp.y].block) { continue; //有障礙,處理下一個節點 } if (temp.curmp < 0) { continue; //沒有移動力了 } if (temp.x < 0 || temp.x >= MAP_MAX_WIDTH || temp.y < 0 || temp.y >= MAP_MAX_HEIGHT) { continue; //出了地圖的范圍 } if (pMap[temp.x][temp.y].flag) { continue; //已經擴展了的結點 } //經過了上面幾層的檢測,沒有問題的節點過濾出來,可以加入AllPath AllPath[nodecount] = temp; } pMap[AllPath[i].x][AllPath[i].y].flag = 1; //將已經擴展的節點標記為已擴展節點 } cutflag = n; //將已擴展節點和待擴展節點的分界線下標值移動到新的分界線 } for (int i = 0; i < nodecount; i) { pMap[AllPath[i].x][AllPath[i].y].bFlag = 0; //標記為已擴展節點的標記設回為待擴展節點。 }
游戲算法整理 算法七 無限大地圖的實現 這已經不是什么新鮮的東西了,不過現在實在想不到什么好寫,而且版面上又異常冷清,我再不說幾句就想要倒閉了一樣。只好暫且拿這個東西來湊數吧。 |