в‘ЎиҝӣиЎҢдёӨдёӨеҪ’тq¶дӢЙи®°еҪ•е…ій”®еӯ—жңүеәҸпјҢеҫ—еҲ° n/2 дёӘй•ҝеәҰдШ“ 2 зҡ„жңүеәҸеӯҗиЎЁпјӣ
в‘ўйҮҚеӨҚ第②жӯҘзӣҙеҲ°жүҖжңүи®°еҪ•еҪ’тq¶жҲҗдёҖдёӘй•ҝеәҰдШ“ n зҡ„жңүеәҸиЎЁдёәжӯўгҖ?br /> дә?еҪ’еЖҲжҺ’еәҸҪҺ—жі•е®һдҫӢ
еҜ№дәҺеҪ’еЖҲжҺ’еәҸҪҺ—жі•ҳqҷзұ»зҡ„еҲҶжІИқ®—жі•пјҢе…¶ж ёеҝғе°ұжҳ?еҲҶи§Ј"е’?йҖ’еҪ’жұӮи§Ј"гҖӮеҜ№дә?еҲҶи§Ј"е®һдҫӢеQҢдјҡеңЁдёӢйқўеҲҶжһҗmsort()ж–ТҺі•дёӯз»ҷеҮәгҖӮжҲ‘们е…ҲзңӢеҗҲтq¶зҡ„ҳqҮзЁӢгҖ?br /> д»ҘдёӢйқўжҸҸҳq°зҡ„еәҸеҲ—дёЮZҫӢеQҢеңЁзҙўеј•иҢғеӣҙеҶ…[first , last)зҡ„еәҸеҲ—иҝҳжңүд№қдёӘж•ҙж•°е…ғзҙ пјҢе®ғз”ұзҙўеј•иҢғеӣҙдёә[first , mid]зҡ„еӣӣдёӘе…ғзҙ жңүеәҸеӯҗеҲ—иЎЁAе’ҢзғҰеј•иҢғеӣҙ[mid , last]зҡ„дә”дёӘе…ғзҙ жңүеәҸеӯҗеҲ—иЎЁBҫl„жҲҗгҖ?br />

жӯҘйӘӨ1еQҡжҜ”иҫғarr[indexA]=7дёҺarr[indexB]=12гҖӮе°Ҷиҫғе°Ҹзҡ„е…ғзҙ?еӨҚеҲ¶еҲ°ж•°ҫl„tempArrзҡ„зғҰеј•indexCеӨ„гҖӮеЖҲһ®ҶindexAе’ҢindexCйғҪжҢҮеҗ‘дёӢдёҖдёӘдҪҚҫ|®гҖ?br />

жӯҘйӘӨ2еQҡжҜ”иҫғarr[indexA]=10дёҺarr[indexB]=12гҖӮе°Ҷиҫғе°Ҹзҡ„е…ғзҙ?0еӨҚеҲ¶еҲ°ж•°ҫl„tempArrзҡ„зғҰеј•indexCеӨ„гҖӮеЖҲһ®ҶindexAе’ҢindexCйғҪжҢҮеҗ‘дёӢдёҖдёӘдҪҚҫ|®гҖ?br />

жӯҘйӘӨ3еQҡжҜ”иҫғarr[indexA]=19дёҺarr[indexB]=12гҖӮе°Ҷиҫғе°Ҹзҡ„е…ғзҙ?2еӨҚеҲ¶еҲ°ж•°ҫl„tempArrзҡ„зғҰеј•indexCеӨ„гҖӮеЖҲһ®ҶindexBе’ҢindexCйғҪжҢҮеҗ‘дёӢдёҖдёӘдҪҚҫ|®гҖ?br />
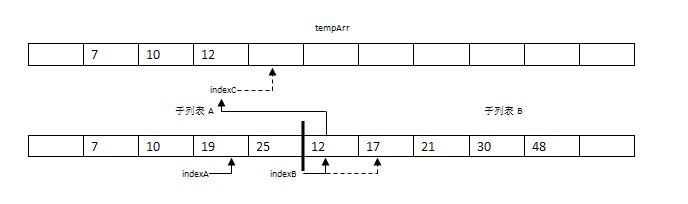
жӯҘйӘӨ4-7еQҡдҫқӢЖЎжҲҗеҜТҺҜ”иҫғдёӨеӯҗиЎЁзҡ„е…ғзҙ е°Ҷ17еQ?9еQ?1еQ?5еӨҚеҲ¶еҲ°ж•°ҫl„tempArrгҖӮжӯӨж—УһјҢindexAеҲ°иҫҫеӯҗиЎЁAзҡ„жңӘһ®?indexA = mid)еQҢindexBеј•з”Ёзҡ„еҖйgШ“30гҖ?br />

жӯҘйӘӨ8-9еQҡе°ҶжңӘеҲ°һ®щNғЁзҡ„еӯҗиЎЁеү©дҪҷж•°жҚ®еӨҚеҲ¶еҲ°tempArrдёӯгҖ?br />

жӯҘйӘӨ10еQҡе°ҶtempArrеӨҚеҲ¶еҲ°еҺҹе§Ӣж•°жҚ®arrдёӯгҖ?br />

дё?еҪ’еЖҲжҺ’еәҸҪҺ—жі•зҡ„е®һзҺ?br /> дәҶи§ЈдәҶеҗҲтq¶иҝҮҪEӢпјҢйӮЈд№ҲзҗҶи§ЈдёӢйқўзҡ„д»Јз ҒеЖҲдёҚжҳҜдёҖд»үҷҡҫдәӢгҖӮдёӢйқўжҸҗдҫӣдәҶеҪ’еЖҲҪҺ—жі•зҡ„йқһжіӣеһӢзүҲжң¬е’ҢжіӣеһӢзүҲжң¬гҖ?br />
 public class MergeSort {
public class MergeSort {
 public static void sort(Object[] arr) {
public static void sort(Object[] arr) { //create a temporary array to store partitioned elements
//create a temporary array to store partitioned elements Object[] tempArr = arr.clone();
Object[] tempArr = arr.clone();
 //call msort with arrays arr and tempArr along
//call msort with arrays arr and tempArr along //with the index range
//with the index range msort(arr, tempArr, 0, arr.length);
msort(arr, tempArr, 0, arr.length); }
}
 public static <T extends Comparable<? super T>> void sort(T[] arr) {
public static <T extends Comparable<? super T>> void sort(T[] arr) { //create a temporary aray to store partitioned elements
//create a temporary aray to store partitioned elements T[] tempArr = (T[]) arr.clone();
T[] tempArr = (T[]) arr.clone();
 //call msort with arrays arr and tempArr along
//call msort with arrays arr and tempArr along //with the index range
//with the index range msort(arr, tempArr, 0, arr.length);
msort(arr, tempArr, 0, arr.length); }
}
 private static void msort(Object[] arr, Object[] tempArr, int first,
private static void msort(Object[] arr, Object[] tempArr, int first, int last) {
int last) { //if the sublist has more than 1 element continue
//if the sublist has more than 1 element continue if (first + 1 < last) {
if (first + 1 < last) { //for sublists of size 2 or more, call msort()
//for sublists of size 2 or more, call msort() //for the left and right sublists and than
//for the left and right sublists and than //merge the sorted sublists using merge()
//merge the sorted sublists using merge() int midpt = (last + first) / 2;
int midpt = (last + first) / 2;
 msort(arr, tempArr, first, midpt);
msort(arr, tempArr, first, midpt); msort(arr, tempArr, midpt, last);
msort(arr, tempArr, midpt, last);
 //if list is already sorted, just copy src to
//if list is already sorted, just copy src to //dest; this is an optimization that results in faster
//dest; this is an optimization that results in faster //sorts for nearly ordered lists
//sorts for nearly ordered lists if (((Comparable) arr[midpt - 1]).compareTo(arr[midpt]) <= 0)
if (((Comparable) arr[midpt - 1]).compareTo(arr[midpt]) <= 0) return;
return; //the elements in the ranges [first,mid] and
//the elements in the ranges [first,mid] and //[mid,last] are ordered;merge the ordered sublists
//[mid,last] are ordered;merge the ordered sublists //into an ordered sequence in the range [first , last]
//into an ordered sequence in the range [first , last] //using the temporary array
//using the temporary array int indexA, indexB, indexC;
int indexA, indexB, indexC;
 //set indexA to scan sublist A with rang [first , mid]
//set indexA to scan sublist A with rang [first , mid] //and indexB to scan sublist B with rang [mid , last]
//and indexB to scan sublist B with rang [mid , last] indexA = first;
indexA = first; indexB = midpt;
indexB = midpt; indexC = first;
indexC = first;
 //while both sublists are not exhausted, compare
//while both sublists are not exhausted, compare //arr[indexA] and arr[indexB]; copy the smaller
//arr[indexA] and arr[indexB]; copy the smaller //to tempArr
//to tempArr while (indexA < midpt && indexB < last) {
while (indexA < midpt && indexB < last) { if (((Comparable) arr[indexA]).compareTo(arr[indexB]) < 0) {
if (((Comparable) arr[indexA]).compareTo(arr[indexB]) < 0) { tempArr[indexC] = arr[indexA]; //copyto tempArr
tempArr[indexC] = arr[indexA]; //copyto tempArr indexA++; //increment indexA
indexA++; //increment indexA } else {
} else { tempArr[indexC] = arr[indexB]; //copyto tempArr
tempArr[indexC] = arr[indexB]; //copyto tempArr indexB++; //increment indexB
indexB++; //increment indexB }
} indexC++; //increment indexC
indexC++; //increment indexC }
} //copy the tail of the sublist that is not exhausted
//copy the tail of the sublist that is not exhausted while (indexA < midpt) {
while (indexA < midpt) { tempArr[indexC++] = arr[indexA++]; //copy to tempArr
tempArr[indexC++] = arr[indexA++]; //copy to tempArr } while (indexB < last) {
} while (indexB < last) { tempArr[indexC++] = arr[indexB++]; //copy to tempArr
tempArr[indexC++] = arr[indexB++]; //copy to tempArr }
} //copy elements form temporary array to original array
//copy elements form temporary array to original array for (int i = first; i < last; i++)
for (int i = first; i < last; i++) arr[i] = tempArr[i];
arr[i] = tempArr[i]; }
} }
} }
}дёҠиҝ°д»Јз ҒдёӯжңҖж ёеҝғзҡ„msort()ж–ТҺі•жҳҜдёҖйҖ’еҪ’ҪҺ—жі•гҖӮдёӢеӣҫиҜҙжҳҺдәҶmsort()ж–ТҺі•дёӯеӯҗеҲ—иЎЁзҡ„еҲҶеүІдёҺеҗҲеЖҲгҖ?nbsp;
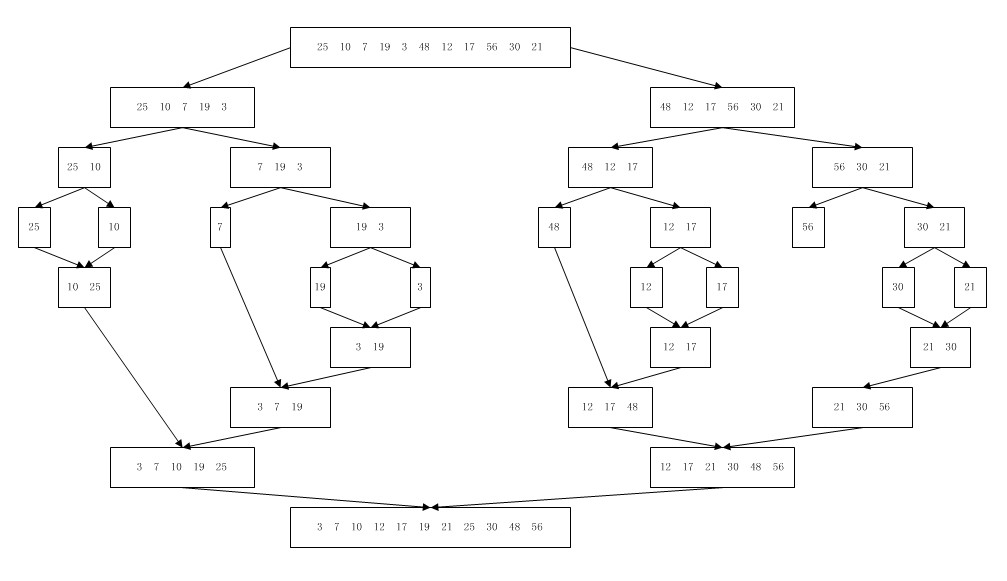
еӣ?еҪ’еЖҲжҺ’еәҸҪҺ—жі•зҡ„ж•ҲзҺ?br /> еҪ’еЖҲжҺ’еәҸзҡ„жңҖеқҸжғ…еҶөдёҺтqӣ_қҮжғ…еҶөҳqҗиЎҢж—үҷ—ҙйғҪдШ“O(nlog2n)гҖӮеҒҮе®ҡж•°ҫl„е…·жңүn=2kдёӘе…ғзҙ гҖӮеҰӮдёӢеӣҫеQ?br />

еңЁеұӮж•?дёҠеҜ№msort()ж–ТҺі•зҡ„第дёҖдёӘи°ғз”Ёдјҡдә§з”ҹдёӨдёӘйҖ’еҪ’и°ғз”ЁеQҢиҝҷдёӨдёӘйҖ’еҪ’и°ғз”Ёдә§з”ҹй•ҝеәҰдёәn/2зҡ„дёӨдёӘеҚҠйғЁеҲҶеҲ—иЎЁеQҢиҖҢmerge()ж–ТҺі•һ®ҶдёҠҳqоCёӨдёӘеҚҠйғЁеҲҶеҲ—иЎЁҫl„еҗҲзҡ„дёҖдёӘжңүеәҸзҡ„nе…ғзҙ еҲ—иЎЁеQӣеңЁеұӮж•°1дёҠеӯҳеңЁдёӨдёӘmsort()ж–ТҺі•зҡ„и°ғз”ЁпјҢжҜҸдёӘи°ғз”ЁеҸҲдјҡдә§з”ҹеҸҰеӨ–дёӨдёӘеҜҡw•ҝеәҰдШ“n/4зҡ„еҲ—иЎЁзҡ„йҖ’еҪ’и°ғз”ЁгҖӮжҜҸдёӘеҗҲтq¶дјҡһ®ҶдёӨдёӘй•ҝеәҰдШ“n/4зҡ„еӯҗеҲ—иЎЁҳqһжҺҘдёЮZёҖдёӘй•ҝеәҰдШ“n/2зҡ„жңүеәҸеҲ—иЎЁпјӣеңЁеұӮж•?дёҠеӯҳеңЁеҜ№merge()ж–ТҺі•зҡ?=22дёӘи°ғз”ЁпјҢжҜҸдёӘи°ғз”ЁдјҡеҲӣе»ЮZёҖдёӘй•ҝеәҰдШ“n/4зҡ„жңүеәҸеҲ—иЎЁгҖӮйҖҡеёёеQҢеңЁеұӮж•°iдёҠеӯҳеңЁеҜ№merge()ж–ТҺі•зҡ?iдёӘи°ғз”ЁпјҢжҜҸдёӘи°ғз”ЁдјҡеҲӣе»ЮZёҖдёӘй•ҝеәҰдШ“n/2iзҡ„жңүеәҸеӯҗеҲ—иЎЁгҖ?br /> еұӮж•°0еQҡеӯҳеңЁеҜ№merge()ж–ТҺі•зҡ?=20ӢЖЎи°ғз”ЁгҖӮиҝҷдёӘи°ғз”ЁеҜ№nдёӘе…ғзҙ жҺ’еәҸгҖ?br /> еұӮж•°1еQҡеӯҳеңЁеҜ№merge()ж–ТҺі•зҡ?=21ӢЖЎи°ғз”ЁгҖӮиҝҷдёӘи°ғз”ЁеҜ№n/2дёӘе…ғзҙ жҺ’еәҸгҖ?br /> еұӮж•°2еQҡеӯҳеңЁеҜ№merge()ж–ТҺі•зҡ?=22ӢЖЎи°ғз”ЁгҖӮиҝҷдёӘи°ғз”ЁеҜ№n/4дёӘе…ғзҙ жҺ’еәҸгҖ?br /> ......
еұӮж•°iеQҡеӯҳеңЁеҜ№merge()ж–ТҺі•зҡ?iӢЖЎи°ғз”ЁгҖӮиҝҷдёӘи°ғз”ЁеҜ№n/iдёӘе…ғзҙ жҺ’еәҸгҖ?br /> еңЁж ‘дёӯзҡ„жҜҸдёҖеұӮпјҢеҗҲеЖҲж¶үеҸҠе…дhңүҫUҝжҖ§иҝҗиЎҢж—¶й—ҙзҡ„n/2iдёӘе…ғзҙ пјҢҳqҷдёӘҫUҝжҖ§иҝҗиЎҢж—¶й—ҙйңҖиҰҒе°‘дәҺn/2iӢЖЎзҡ„жҜ”иҫғгҖӮеңЁеұӮж•°iдёҠз»„еҗҲзҡ„2iдёӘеҗҲтq¶ж“ҚдҪңйңҖиҰҒе°‘дә?i*n/2i=nӢЖЎзҡ„жҜ”иҫғгҖӮеҒҮе®ҡn=2k,еҲҶеүІҳqҮзЁӢдјҡеңЁn/2k=1зҡ„kеұӮж•°дёҠз»ҲжӯўгҖӮйӮЈд№ҲжүҖжңүеұӮдёҠе®ҢжҲҗзҡ„е·ҘдҪңжҖ»йҮҸдё?k*n = nlog2nгҖӮеӣ жӯӨmsort()ж–ТҺі•зҡ„жңҖеқҸжғ…еҶү|•ҲзҺҮдШ“O(nlog2n)гҖ?
Brian 2008-06-13 00:54 еҸ‘иЎЁиҜ„и®ә
]]>еҒҮе®ҡҳqҷдёӘж•°з»„зҡ„еәҸжҳҜжҺ’еҘҪзҡ„еQҢ然еҗҺд»ҺеӨҙеҫҖеҗҺпјҢеҰӮжһңжңүж•°жҜ”еҪ“еүҚеӨ–еұӮе…ғзҙ зҡ„еҖјеӨ§еQҢеҲҷһ®ҶиҝҷдёӘж•°зҡ„дҪҚҫ|®еҫҖеҗҺжҢӘеQҢзӣҙеҲ°еҪ“еүҚеӨ–еұӮе…ғзҙ зҡ„еҖјеӨ§дәҺжҲ–иҖ…зӯүдәҺе®ғеүҚйқўзҡ„дҪҚҫ|®дШ“жӯўгҖ?br /> дә?жҸ’е…ҘжҺ’еәҸҪҺ—жі•е®һдҫӢ
з”Ёдә”дёӘеҗҚеӯ?Monroe,Chin,Flores,Steinе’ҢDare)зҡ„еҲ—иЎЁзҡ„жҸ’е…ҘжҺ’еәҸҪҺ—жі•дёЮZҫӢеQ?br /> Monroe д»ҺMonroeејҖе§?br />
еӨ„зҗҶеҗҚеӯ—Chin Chine Monroe һ®ҶChinжҸ’е…ҘеҲоCҪҚҫ|?еQӣMonroeҝUХdҠЁиҮідҪҚҫ|?
еӨ„зҗҶеҗҚеӯ—Flores Chine Flores Monroe һ®ҶFloresжҸ’е…ҘеҲоCҪҚҫ|?еQӣMonroeҝUХdҠЁиҮідҪҚҫ|?
еӨ„зҗҶеҗҚеӯ—Stein Chine Flores Monroe Stein SteinдҪҚзҪ®жӯЈзЎ®
еӨ„зҗҶеҗҚеӯ—Dare Chine Dare Flores Monroe Stein һ®ҶDareжҸ’е…ҘеңЁдҪҚҫ|?еQӣеҲ—иЎЁе°ҫйғЁеҗ‘еҸіз§»еҠ?nbsp;
дё?жҸ’е…ҘжҺ’еәҸҪҺ—жі•зҡ„е®һзҺ?br />
 public class InsertSort {
public class InsertSort { //sort an array of elements using insertion sort
//sort an array of elements using insertion sort public static <T extends Comparable<? super T>> void sort(T[] arr) {
public static <T extends Comparable<? super T>> void sort(T[] arr) { int i, j, n = arr.length;
int i, j, n = arr.length; T target;
T target;
 /**
/** * place element at index i into the sublist
* place element at index i into the sublist * from index 0 to i-1 where 1<= i,
* from index 0 to i-1 where 1<= i, * so it is in the correct positon
* so it is in the correct positon */
*/ for (i = 1; i < n; i++) {
for (i = 1; i < n; i++) { //index j scans down list from index i looking for
//index j scans down list from index i looking for //correct position to locate target; assigns it to
//correct position to locate target; assigns it to //arr at index j
//arr at index j j = i;
j = i; target = arr[i];
target = arr[i]; //locate insertion point by scanning downward as long
//locate insertion point by scanning downward as long //as target < arr[j] and we have not encountered the
//as target < arr[j] and we have not encountered the //beginning of the array
//beginning of the array while (j > 0 && target.compareTo(arr[j - 1]) < 0) {
while (j > 0 && target.compareTo(arr[j - 1]) < 0) { //shift elements up list to make room for insertion
//shift elements up list to make room for insertion arr[j] = arr[j - 1];
arr[j] = arr[j - 1]; j--;
j--; }
} //the location is found;insert target
//the location is found;insert target arr[j] = target;
arr[j] = target; }
} }
} }
}еӣ?жҸ’е…ҘжҺ’еәҸҪҺ—жі•зҡ„ж•ҲзҺ?br /> еҒҮе®ҡnжҳҜж•°ҫl„зҡ„й•ҝеәҰеQҢйӮЈд№ҲжҸ’е…ҘжҺ’еәҸйңҖиҰҒn-1йҒҚгҖӮеҜ№дәҺйҖҡз”Ёзҡ„йҒҚiжқҘиҜҙеQҢжҸ’е…Ҙж“ҚдҪңд»Һarr[0]еҲ°arr[i-1]зҡ„еӯҗеҲ—иЎЁдёӯпјҢтq¶дё”йңҖиҰҒег^еқҮi/2ӢЖЎжҜ”иҫғгҖӮжҜ”иҫғзҡ„тqӣ_қҮжҖАL•°дёәпјҡ
T(n) = 1/2 + 2/2 + 3/2 + ...... + (n-2)/2 + (n-1)/2 = n(n-1)/4
ж ТҺҚ®T(n)зҡ„дё»ҷе№пјҢжҸ’е…ҘжҺ’еәҸҪҺ—жі•зҡ„ег^еқҮиҝҗиЎҢж—¶й—ҙдШ“O(n2)гҖӮжңҖеҘҪжғ…еҶөдШ“O(n)еQҢжңҖеқҸжғ…еҶөдШ“O(n2)гҖ?
Brian 2008-06-11 23:56 еҸ‘иЎЁиҜ„и®ә
]]>

