Sorting algorithms --Selection Sort
Posted on 2011-05-06 16:16 ytl 閱讀(398) 評論(0) 編輯 收藏 所屬分類: Algorithms and programming concepts
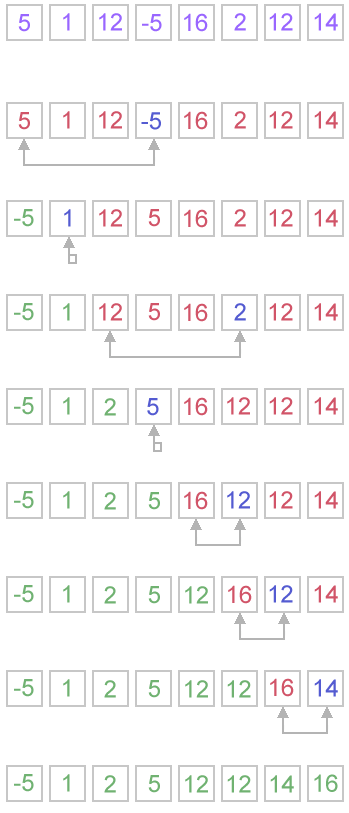
Selection SortSelection sort is one of the O(n2) sorting algorithms, which makes it quite inefficient for sorting large data volumes. Selection sort is notable for its programming simplicity and it can over perform other sorts in certain situations (see complexity analysis for more details). AlgorithmThe idea of algorithm is quite simple. Array is imaginary divided into two parts - sorted one and unsorted one. At the beginning, sorted part is empty, while unsorted one contains whole array. At every step, algorithm finds minimal element in the unsorted part and adds it to the end of the sorted one. When unsorted part becomes empty, algorithmstops. When algorithm sorts an array, it swaps first element of unsorted part with minimal element and then it is included to the sorted part. This implementation of selection sort in not stable. In case of linked list is sorted, and, instead of swaps, minimal element is linked to the unsorted part, selection sort is stable. Let us see an example of sorting an array to make the idea of selection sort clearer. Example. Sort {5, 1, 12, -5, 16, 2, 12, 14} using selection sort.
Complexity analysisSelection sort stops, when unsorted part becomes empty. As we know, on every step number of unsorted elements decreased by one. Therefore, selection sort makes n steps (n is number of elements in array) of outer loop, before stop. Every step of outer loop requires finding minimum in unsorted part. Summing up, n + (n - 1) + (n - 2) + ... + 1, results in O(n2) number of comparisons. Number of swaps may vary from zero (in case of sorted array) to n - 1 (in case array was sorted in reversed order), which results in O(n) number of swaps. Overall algorithm complexity is O(n2). Fact, that selection sort requires n - 1 number of swaps at most, makes it very efficient in situations, when write operation is significantly more expensive, than read operation. Code snippetsJavapublic void selectionSort(int[] arr) { int i, j, minIndex, tmp; int n = arr.length; for (i = 0; i < n - 1; i++) { minIndex = i; for (j = i + 1; j < n; j++) if (arr[j] < arr[minIndex]) minIndex = j; if (minIndex != i) { tmp = arr[i]; arr[i] = arr[minIndex]; arr[minIndex] = tmp; } } } Python for i in range(len(L)-1): minIndex = i minValue = L[i] j = i + 1 while j< len(L): if minValue > L[j]: minIndex = j minValue = L[j] j += 1 if minIndex != i: temp = L[i] L[i] = L[minIndex] L[minIndex] = temp
|