人在江湖

:: 管理

82 Posts :: 10 Stories :: 169 Comments :: 0 Trackbacks

相關概念：

相對誤差（Relative Error）：絕對誤差與真值的比值

所謂殘差（residual error），應該是在回歸時，實際y值與回歸曲線得到的理論y值之間的差值。標準殘差，就是各殘差的標準方差。

異方差性（heteroscedasticity ）是為了保證回歸參數估計量具有良好的統計性質，經典線性回歸模型的一個重要假定是：總體回歸函數中的隨機誤差項滿足同方差性，即它們都有相同的方差。如果這一假定不滿足，則稱線性回歸模型存在異方差性。

條件方差（Conditional variance）：只要把原來求方差時的概率密度函數換成條件密度函數就行了意義就是當X發生時，Y發生的方差

自相關函數（Autocorrelation function，縮寫ACF）：

將一個有序的隨機變量系列與其自身相比較，這就是自相關函數在統計學中的定義。每個不存在相位差的系列，都與其自身相似，即在此情況下，自相關函數值最大。如果系列中的組成部分相互之間存在相關性（不再是隨機的），則由以下相關值方程所計算的值不再為零，這樣的組成部分為自相關。

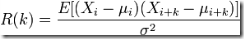
E ......... 期望值。

X_i ........ 在t(i)時的隨機變量值。

μ_i ........ 在t(i)時的預期值。

X_{i + k} .... 在t(i+k)時的隨機變量值。

μ_{i + k} .... 在t(i+k)時的預期值。

σ² ......... 為方差。

所得的自相關值R的取值范圍為[-1,1],1為最大相關值，-1則為最大不相關值。

白噪聲序列：

隨機變量X（t）（t=1，2，3……），如果是由一個不相關的隨機變量的序列構成的，即對于所有S不等于T，隨機變量Xt和Xs的協方差均為零，則稱其為純隨機過程。對于一個純隨機過程來說，若其期望和方差均為常數，則稱之為白噪聲過程。白噪聲過程的樣本實稱成為白噪聲序列，簡稱白噪聲。之所以稱為白噪聲，是因為他和白光的特性類似，白光的光譜在各個頻率上有相同的強度，白噪聲的譜密度在各個頻率上的值相同。

差分：差分有前向差分和后向差分。前向差分：函數的前向差分通常簡稱為函數的差分。對于函數，如果：

，

則稱為的一階前向差分。只所以稱為前向差分是因為以x為參考點，x+1在x的前面。逆向差分：對于函數f(x)，如果：

則稱為的一階逆向差分。

時間序列的特征

非平穩性（nonstationarity，也譯作不平穩性，非穩定性）：即時間序列變量無法呈現出一個長期趨勢并最終趨于一個常數或是一個線性函數

波動幅度隨時間變化（Time－varying Volatility）：即一個時間序列變量的方差隨時間的變化而變化

雖然單獨看不同的時間序列變量可能具有非穩定性，但按一定結構組合后的新的時間序列變量卻可能是穩定的，即這個新的時間序列變量長期來看，會趨向于一個常數或是一個線性函數。例如，時間序列變量X(t)非穩定，但其二階差分卻可能是穩定的；時間序列變量X(t)和Y(t)非穩定，但線性組合X(t)-bY(t)卻可能是穩定的。

時間序列分析通常是把各種可能發生作用的因素進行分類，傳統的分類方法是按各種因素的特點或影響效果分為四大類：(1)長期趨勢；(2)季節變動；(3)循環變動；(4)不規則變動。

時間序列預測法種類，

1. 簡單序時平均數法算術平均法

2. 移動平均法：移動平均法是一種簡單平滑預測技術，它的基本思想是：根據時間序列資料、逐項推移，依次計算包含一定項數的序時平均值，以反映長期趨勢的方法。

分為簡單移動平均法，加權移動平均法。一般而言，最近期的數據最能預示未來的情況，因而權重應大些。

移動平均法的優缺點

　　使用移動平均法進行預測能平滑掉需求的突然波動對預測結果的影響。但移動平均法運用時也存在著如下問題：

　　1、加大移動平均法的期數（即加大n值）會使平滑波動效果更好，但會使預測值對數據實際變動更不敏感；

　　2、移動平均值并不能總是很好地反映出趨勢。由于是平均值，預測值總是停留在過去的水平上而無法預計會導致將來更高或更低的波動；

　　3、移動平均法要由大量的過去數據的記錄。

使用移動平均法時，主要是要定下來N（用幾個時期預測下個時期）是多少，實際中可以取多個N然后比相對誤差。

3. 指數平滑法：所有預測方法中，指數平滑是用得最多的一種。簡單的全期平均法是對時間數列的過去數據一個不漏地全部加以同等利用；移動平均法則不考慮較遠期的數據，并在加權移動平均法中給予近期資料更大的權重；而指數平滑法則兼容了全期平均和移動平均所長，不舍棄過去的數據，但是僅給予逐漸減弱的影響程度，即隨著數據的遠離，賦予逐漸收斂為零的權數。也就是說指數平滑法是在移動平均法基礎上發展起來的一種時間序列分析預測法，它是通過計算指數平滑值，配合一定的時間序列預測模型對現象的未來進行預測。其原理是任一期的指數平滑值都是本期實際觀察值與前一期指數平滑值的加權平均。

指數平滑法的基本公式是：式中，

S_t--時間t的平滑值；
y_t--時間t的實際值；
S_{t − 1}--時間t-1的平滑值；
a--平滑常數，其取值范圍為[0,1]；

指數平滑常數取值至關重要。平滑常數決定了平滑水平以及對預測值與實際結果之間差異的響應速度。平滑常數a越接近于1，遠期實際值對本期平滑值影響程度的下降越迅速；平滑常數a越接近于 0，遠期實際值對本期平滑值影響程度的下降越緩慢。由此，當時間數列相對平穩時，可取較大的a；當時間數列波動較大時，應取較小的a，以不忽略遠期實際值的影響。

據平滑次數不同，指數平滑法分為：一次指數平滑法、二次指數平滑法和三次指數平滑法等。當時間數列無明顯的趨勢變化，可用一次指數平滑預測。

（一）一次指數平滑預測

　　當時間數列無明顯的趨勢變化，可用一次指數平滑預測。其預測公式為：

　　yt+1'=ayt+(1-a)yt' 式中，

yt+1'--t+1期的預測值，即本期（t期）的平滑值St ；
yt--t期的實際值；
yt'--t期的預測值，即上期的平滑值St-1 。

　　該公式又可以寫作：yt+1'=yt'+a(yt- yt')。可見，下期預測值又是本期預測值與以a為折扣的本期實際值與預測值誤差之和。

（二）二次指數平滑預測

　　二次指數平滑是對一次指數平滑的再平滑。它適用于具線性趨勢的時間數列。其預測公式為：

　　yt+m=(2+am/(1-a))yt'-(1+am/(1-a))yt=(2yt'-yt)+m(yt'-yt) a/(1-a)

　　式中，yt= ayt-1'+(1-a)yt-1

　　顯然，二次指數平滑是一直線方程，其截距為：(2yt'-yt)，斜率為：(yt'-yt) a/(1-a),自變量為預測天數。

（三）三次指數平滑預測

　　三次指數平滑預測是二次平滑基礎上的再平滑。其預測公式是：

　　yt+m=(3yt'-3yt+yt)+[(6-5a)yt'-(10-8a)yt+(4-3a)yt]*am/2(1-a)2+ (yt'-2yt+yt')*a2m2/2(1-a)2

　　式中，yt=ayt-1+(1-a)yt-1

　　它們的基本思想都是：預測值是以前觀測值的加權和，且對不同的數據給予不同的權，新數據給較大的權，舊數據給較小的權。

案例:指數平滑法在銷售預算中的應用

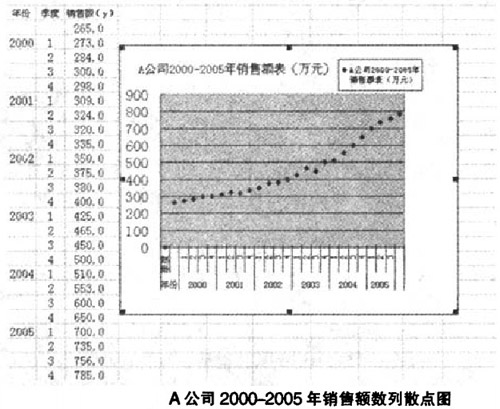
　　某軟件公司A為例。給出2000-2005年的歷史銷售資料，將數據代入指數平滑模型。預測2006年的銷售額，作為銷售預算編制的基礎。

　　由散點圖示可知。根據經驗判斷法。A公司2000-2005年銷售額時間序列波動很大。長期趨勢變化幅度較大，呈現明顯且迅速的上升趨勢，宜選擇較大的α值，可在05-O.8間選值，以使預測模型靈敏度高些，結合試算法取0.5，0.6,0.8分別測試。經過第一次指數平滑后，數列呈現直線趨勢，故選用二次指數平滑法即可。

試算結果見下表。根據偏差平方的均值(MSE)最小，即各期實際值與預測值差的平方和除以總期數．以最小值來確定理的取值的標準，經測算當α = 0.6時，MSE₁ = l445.4；當α = 0.8時，MSE₂=10783.7；當α = 0.5時，MSE₃ = 1906.1。因此選擇α = 0.6來預測2006年4個季度的銷售額。

　　2005年第四季度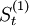 $S_t^{(1)}$ =736.8; 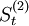$S_t^{(2)}$ =679.5;；可以求得 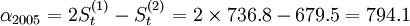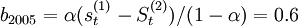$\alpha_{2005}=2S_t^{(1)}-S_t^{(2)}=2\times736.8-679.5=794.1$ ； $b_{2005}=\alpha(s_t^{(1)}-S_t^{(2)})/(1-\alpha)=0.6$ =(736.8-679.5)/0.4=85.9則預測方Y_{2005 + T} = 794.1 + 85.9T,因此，2006年第一、二、三、四季度的預測值分別為：

Y₁ = 794.1 + 85.9 = 800(萬元)

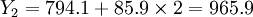$Y_2=794.1+85.9\times2=965.9$ (萬元)

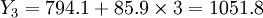$Y_3=794.1+85.9\times3=1051.8$ (萬元)

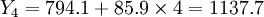$Y_4=794.1+85.9\times4=1137.7$ (萬元)

　　綜上所述，本案例首先根據銷售歷史資料，給出數列散點圖。再根據散點圖的特征選擇二次指數平滑法，通過對α的試算，確定符合預測需要的α值，最后根據指數平滑模型計算出2006年14季度的銷售預測值，作為銷售預算的基礎。

典型模型包括arch模型，arima模型等

arch模型：

ARCH模型的基本思想是指在以前信息集下，某一時刻一個噪聲的發生是服從正態分布。該正態分布的均值為零，方差是一個隨時間變化的量(即為條件異方差)。并且這個隨時間變化的方差是過去有限項噪聲值平方的線性組合(即為自回歸)。這樣就構成了自回歸條件異方差模型。

　　由于需要使用到條件方差，我們這里不采用恩格爾的比較嚴謹的復雜的數學表達式，而是采取下面的表達方式，以便于我們把握模型的精髓。見如下數學表達：

　　Yt = βXt＋εt (1)其中，

Yt為被解釋變量，
Xt為解釋變量，
εt為誤差項。

　　如果誤差項的平方服從AR(q)過程，即εt2 =a0＋a1εt－12 ＋a2εt－22 ＋ …… ＋ aqεt－q2 ＋ηt t =1,2,3…… (2)其中，

　　ηt獨立同分布，并滿足E（ηt）= 0, D(ηt)= λ2 ,則稱上述模型是自回歸條件異方差模型。簡記為ARCH模型。稱序列εt 服從q階的ARCH的過程，記作εt －ARCH(q)。為了保證εt2 為正值，要求a0 >0 ,ai ≥0 i=2,3,4… 。

　　上面（1）和（2）式構成的模型被稱為回歸－ARCH模型。ARCH模型通常對主體模型的隨機擾動項進行建模分析。以便充分的提取殘差中的信息，使得最終的模型殘差ηt成為白噪聲序列。

　　從上面的模型中可以看出，由于現在時刻噪聲的方差是過去有限項噪聲值平方的回歸，也就是說噪聲的波動具有一定的記憶性，因此，如果在以前時刻噪聲的方差變大，那么在此刻噪聲的方差往往也跟著變大；如果在以前時刻噪聲的方差變小，那么在此刻噪聲的方差往往也跟著變小。體現到期貨市場，那就是如果前一階段期貨合約價格波動變大，那么在此刻市場價格波動也往往較大

GARCH模型是一個專門針對金融數據所量體訂做的回歸模型

arima模型：

Autoregressive Integrated Moving Average Model。 ARIMA（p，d，q）稱為差分自回歸移動平均模型，AR是自回歸, p為自回歸項; MA為移動平均，q為移動平均項數，d為時間序列成為平穩時所做的差分次數。

ARIMA模型預測的基本程序

（一）根據時間序列的散點圖、自相關函數和偏自相關函數圖以ADF單位根檢驗其方差、趨勢及其季節性變化規律，對序列的平穩性進行識別。一般來講，經濟運行的時間序列都不是平穩序列。

　　（二）對非平穩序列進行平穩化處理。如果數據序列是非平穩的，并存在一定的增長或下降趨勢，則需要對數據進行差分處理，如果數據存在異方差，則需對數據進行技術處理，直到處理后的數據的自相關函數值和偏相關函數值無顯著地異于零。

　　（三）根據時間序列模型的識別規則，建立相應的模型。若平穩序列的偏相關函數是截尾的，而自相關函數是拖尾的，可斷定序列適合AR模型；若平穩序列的偏相關函數是拖尾的，而自相關函數是截尾的，則可斷定序列適合MA模型；若平穩序列的偏相關函數和自相關函數均是拖尾的，則序列適合ARMA模型。

　　（四）進行參數估計，檢驗是否具有統計意義。

　　（五）進行假設檢驗，診斷殘差序列是否為白噪聲。

　　（六）利用已通過檢驗的模型進行預測分析。

取對數可以消除數據波動變大趨勢，對數列進行一階差分，可以消除數據增長趨勢性和季節性。

一個例子：

備件消耗預測ARIMA(p,d,q)模型實質是先對非平穩的備件消耗歷史數據Yt進行d（d＝0,1,dots,n）次差分處理得到新的平穩的數據序列Xt，將Xt擬合ARMA(p,q)模型，然后再將原d次差分還原，便可以得到Y_t的預測數據。其中，ARMA(p,q)的一般表達式為：

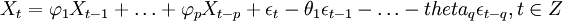$X_t=\varphi_1X_{t-1}+\ldots+\varphi_pX_{t-p}+\epsilon_t-\theta_1\epsilon_{t-1}-\ldots-theta_q\epsilon_{t-q},t\in Z$ 　　(1)

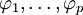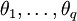　　式中，前半部分為自回歸部分，非負整數p為自回歸階數， $\varphi_1,\ldots,\varphi_p$ 為自回歸系數，后半部分為滑動平均部分，非負整數q為滑動平均階數， $\theta_1,\ldots,\theta_q$ 為滑動平均系數；X_t為備件消耗數據相關序列，ε_t為WN(0,σ²)。

　　當q=0時，該模型成為AR(p)模型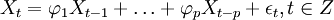： $X_t=\varphi_1X_{t-1}+\ldots+\varphi_pX_{t-p}+\epsilon_t,t\in Z$ 　　(2)

　　當p＝0時，該模型成為MA(q)模型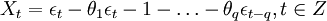： $X_t=\epsilon_t-\theta_1\epsilon_t-1-\ldots-\theta_q\epsilon_{t-q},t\in Z$ 　　(3)

所謂零均值化處理就是取前N組（或全部）數據作為觀測數據，進行零均值化處理，即：，得到一組預處理后的新序列。

SAS與arima：

sas 有proc arima. 分為三個階段：

identification: 識別候選arima模型。

estimation and diagnositic checking: 為模型估計參數，并提供診斷統計信息幫助判斷模型是否好。

forcasting: 預測未來值。

這里有一個proc arima的例子： http://www.docin.com/p-46241714.html

貼一下代碼，生成data set的部分略有改動，copy&paste pdf的數據到txt中，然后批量輸入data set. 方便生成data set

filename input "c:\temp\sun.txt";
data exp1;
   infile input;
   input a1 @@;
   year=intnx('year','1jan1742'd,_n_-1);
   format year year4.;
run;

proc gplot data=exp1;
symbol i=spline v=star h=2 c=green;
plot a1*year;
run;

proc arima data=exp1;
identify var=a1 nlag=24;
run;

estimate p=3;
run;

forecast lead=6 interval=year id=year out=out;
run;
proc print data=out;
run;

vcycyv:

1. nlag取24，在圖上看是一個w型。

2. 書上做identification步驟之后，得出結論：“觀察輸出結果。初步識別序列為 AR(3)模型。” 不確定這個結論是怎么得出來的，1. 怎么算截尾，怎么算拖尾？2. AR（3）里那個3是怎么出來的？對第二個問題瞎猜一下，是看ACF圖觀察出來三個值能推出來第四個值么？

問了學統計的同事，解答了上面兩個問題，還是需要繼續理解：

截尾：是指在ACF或PACF圖中自相關系數和偏自相關系數在滯后的前幾期內處于置信區間之外，而滯后的系數基本上都落入置信區間內，且逐漸趨于0.
拖尾：是指在ACF或PACF圖中自相關系數和偏自相關系數有指數型、正弦型或震蕩型衰減的波動。且都不會落入置信區間內。
至于那個3，因為PACF圖上可以看出當為3時，不在置信區間內

就是那時開始不在藍框內了

并且ACF圖此時為拖尾

參考：

http://wiki.mbalib.com/wiki/%E6%97%B6%E9%97%B4%E5%BA%8F%E5%88%97%E9%A2%84%E6%B5%8B%E6%B3%95

http://wiki.mbalib.com/wiki/%E7%A7%BB%E5%8A%A8%E5%B9%B3%E5%9D%87%E6%B3%95

http://wiki.mbalib.com/wiki/%E6%8C%87%E6%95%B0%E5%B9%B3%E6%BB%91%E6%B3%95

http://zh.wikipedia.org/wiki/%E6%97%B6%E9%97%B4%E5%BA%8F%E5%88%97

http://zh.wikipedia.org/wiki/%E8%87%AA%E7%9B%B8%E5%85%B3%E5%87%BD%E6%95%B0

http://wiki.mbalib.com/wiki/ARIMA%E6%A8%A1%E5%9E%8B

http://www.docin.com/p-46241714.html

SAS help

posted on 2011-09-07 09:44 人在江湖閱讀(3173) 評論(2) 編輯收藏所屬分類: BI

Feedback

# re: 時間序列 2011-09-09 08:23 tb

算法很好學習了回復更多評論

# re: 時間序列 2011-09-13 18:10 -+

你瘋了？回復更多評論

新用戶注冊刷新評論列表


只有注冊用戶登錄后才能發表評論。




網站導航: 博客園 IT新聞 Chat2DB C++博客博問管理
相關文章: 自錄pentaho視頻教程神經網絡決策樹 cluster聚類分析線性回歸矩陣與SAS IML淺嘗輒止時間序列分享讀書筆記 Data Mining Concepts and Techniques Basel2模型驗證二：Kendall tau Basel2模型驗證一：Hosmer–Lemeshow test

人在江湖

公告

常用鏈接

留言簿(16)

隨筆分類(90)

搜索

積分與排名

最新評論

閱讀排行榜