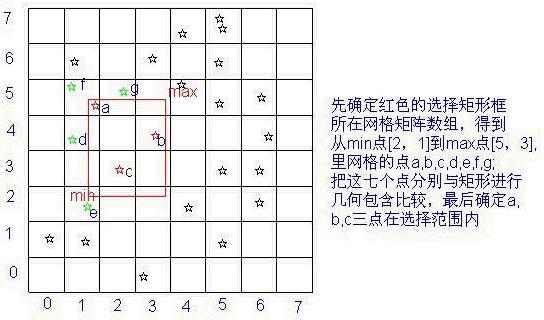
ç°å¨å¤§å®¶å¯¹ç¦å¼æäºææ§è®¤è¯ï¼é£ä»ä¹æ¯“½Iºé´ç´¢å¼“å¢ï¼”½Iºé´ç´¢å¼“ä¹æ¯”索弓åQæ¯å¯¹ç©ºé´å¾å½¢éååçä¸ä¸?#8221;ç®å½“åQæé«å¨q个åÖÅéåä¸æ¥æ¾æ个å¾å½¢å¯¹è±¡çæçãæ¯å¦è¯´åQæ们å¨ä¸ä¸ªå°åÖ¾å±ä¸qè¡ç©åÅéæ©åQç¡®å®è¿ä¸ªå¾å±ä¸åªäºåÖ è¢«è¿ä¸ªç©å½¢æå®å ¨å å«å¢ï¼å¨æ²¡æ?#8221;½Iºé´ç´¢å¼“çæ åµä¸åQæ们ä¼æè¿ä¸ªå¾å±ä¸çææå¾å ï¼ä¸ä¸æ¿æ¥ä¸è¿ä¸ªç©å½¢è¿è¡å ä½ä¸çå å«å¤æï¼ä»¥ç¡®å®å°åºåªäºå¾å 被å®å ¨å å«å¨è¿ä¸ªç©å½¢å ãæ¨æ¯ä¸æ¯è§å¾è¿æ ·åå¾åçå¢åQå ¶å®ä¸çÓ¼æ们å çä¸ä¸ªç½æ ¼ç¦å¼çä¾ååQ?/p>
æ们对è¿ä¸ªç¹åÖ±ä½äº¾|æ ¼ç´¢å¼åQå¤æåªäºç¹å¨è¿ä¸ªç©å½¢éæ©æ¡å åQæ¯ä¸éè¦æq个åÖ±éææççw½è¦ä¸ç©åÅqè¡å ä½å å«qç®çï¼åªå¯¹a,b,c,d,e,f,gqä¸ä¸ªç¹åäºqç®ãå¯ä»¥æ¨æ³ä¸ä¸ï¼å¦æä¸ä¸ªç¹åÖ±æåä¸ä¸ªç¹ï¼ä¸å¾ç«ç©ºé´ç¦å¼ï¼ä»ÖM½å°å¾æä½é½å°å¯Ò´ä¸ªå¾å±çææå¾å éåä¸Æ¡ï¼ä¹å°±æ¯è¦For循ç¯10ä¸æ¬¡åQå¾ç«ç¦å¼å°ä½¿å¾For循ç¯ç次æîC¸éå¾å¤å¾å¤ï¼æçèªç¶æé«å¾å¤åQ?/p>
åµåµ…æ_¿ 大家é½ç¥é空é´ç¦å¼ç好å¤äºï¼ä¹ä¸ç¥ä¸è§å大家ä»ç»äºç¹åÖ±çç½æ ¼ç¦å¼ï¼qæåªäºå¸¸ç¨ç空é´ç¦å¼å¢åQè¿äºç©ºé´ç¦å¼å该å¦ä½å®ç°å¢åQ带çqæ ·çé®é¢ï¼ä¸é¢ä»ç»å ç§å¸¸ç¨ç空é´ç¦å¼ã?/p>
¾|æ ¼ç´¢å¼
¾|æ ¼ç´¢å¼®±æ¯å¨ä¸ä¸ªå°åÖ¾å±ä¸åQææ¯ä¸ª®ç½æ ¼å®½â³w,é«â³hæä¸ååçæ ¼¾|ï¼è®¡ç®æ¯ä¸ªåÖ
æå æ®çç½æ ¼æè
æ¾lè¿çç½æ ¼åå
éåï¼
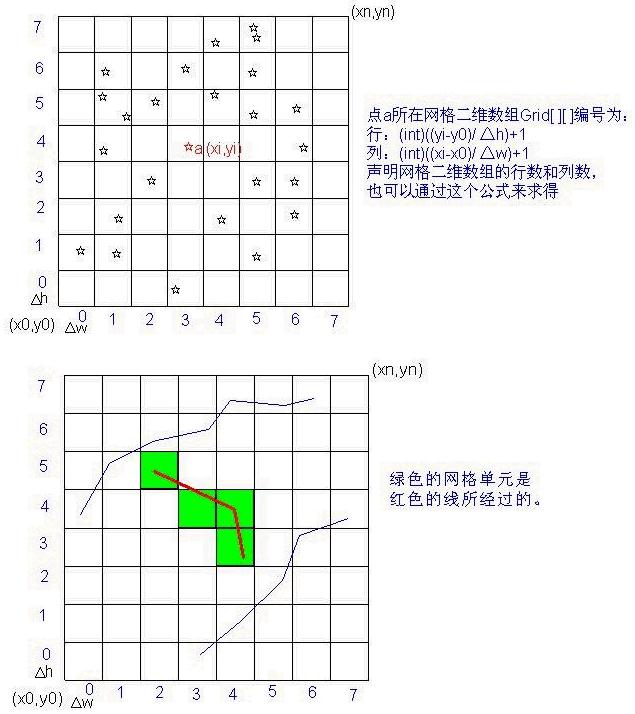
å¨è¿äºç½æ ¼åå ä¸åQè®°å½ä¸åÖ å¯¹è±¡çå°åæè å¼ç¨ï¼æ¯å¦åQ声æä¸ä¸ªå¯¹è±¡äº¾l´æ°¾l?font face="Times New Roman"> List grid[m][n]; m代表¾|æ ¼çè¡æͼn代表¾|æ ¼çåæͼæ¯ä¸ªæ°ç»å ç´ ä¸ÞZ¸ä¸?#8220;éå对象”åQç¨äºåå¨è¿ä¸ªç½æ ¼åå æå çææå¾å çå°åæå¼ç¨ï¼qæ ·¾|æ ¼ç´¢å¼®±å¾ç«å¥½äºãä¸ä¸æ¥ï¼æ们该æä¹ç¨è¿ä¸ªç½æ ¼ç¦å¼å¢åQ?span style="font-size: 10.5pt">ææçåÖÅ桤ºåæä½é½å¯ä»¥åå©äº?#8220;½Iºé´ç´¢å¼”æ¥æé«æçãäDå 个ä¾åæ¥è¯´æ?#8220;½Iºé´ç´¢å¼“çäÉç¨ï¼
1åQç¡®å®æçȩ形左ä¸è§åå³ä¸è§æå¨ç¾|æ ¼æ°ç»å ç´ åQå³å¯å¾å°è¿ä¸ªç©å½¢æå è¦ççææç½æ ¼éåï¼
2åQéåè¿ä¸ªç½æ ¼éåä¸çå ç´ ï¼åå°æ¯ä¸ª¾|æ ¼å ç´ Listä¸æè®°å½çå¾å ï¼
3åQç»åø¿äºå¾å å³å¯ãï¼å½ç¶æ´ä¸ªqç¨æ¶ååîC¸¤ç¹ï¼1åQå±òqåæ åå°å¾åæ çäºç¸åæ¢ï¼2åQçªå£è£åï¼ä¹å¯ä»¥ä¸è£ååQ?/p>
äºã?/font>å å«å¤æåQç»åÞZ¸ä¸ªç¹pointåä¸ä¸ªå¤è¾¹åÅpolygonåQå¤æç¹æ¯å¦å¨é¢å ï¼é¦å å¤æq个çÒå¨ç¾|æ ¼åQæ¯å¦åæ¶å ³èè¿ä¸?font face="Times New Roman">polygonåQå¦æä¸æ¯ï¼è¡¨æç¹ä¸å¨é¢å ï¼å¦ææ¯ï¼å¯ä»¥ä¸ä¸æ¥ç¾_¡¡®è§£æå ä½å¤æåQæè 精度å 许çæ åµä¸ï¼å_¤æ?font face="Times New Roman">polygonæ¯å å?font face="Times New Roman">pointçã?/p>
å¦å¤åQ?font face="Times New Roman">Google Mapåºè¯¥ä¹æ¯éç¨å°ç¾|æ ¼çæ¹å¼ï¼å¯¹å°å־象è¿è¡ç¦å¼çåQå¯è§ä¸æï¼¾|æ ¼ç´¢å¼å¨å¾å½¢æ¾½Cºï¼éæ©åQææå¤æä¸ç广æ³åºç¨ãä½åæ¶ä¹åå¨å¾ä¸¥éç缺éøP¼å½è¢«ç´¢å¼çå¾å 对象毾U¿ï¼æè å¤è¾¹åÅçæ¶åï¼åå¨ç´¢å¼çåä½ï¼å³ä¸ä¸ªçº¿æè å¤è¾¹åÅçå¼ç¨å¨å¤ä¸ª¾|æ ¼ä¸é½æè®°å½ãéçåä½éçå¢å¤§åQæçææ¾ä¸éãæ以ï¼å¾å¤å¦è æåÞZºåç§æÒ³æ¥æ¹qç½æ ¼ç¦å¼ï¼q个®å¨ä¸é¢çç« èä¸ä»ç»ãèç¹åÖ é常éå¾|æ ¼ç´¢å¼åQä¸åå¨åä½é®é¢ã?/p>
ååæ ç¦å¼ï¼QuadtreeåQ?/span>
¾cÖM¼¼äºåé¢ä»¾lç¾|æ ¼ç´¢å¼,ä¹æ¯å¯¹å°ç空é´è¿è¡ç½æ ¼ååï¼å¯¹å°ç空é´éå½qè¡ååæ¥æ建ååæ åQæ¬æå°å¨æ®éååæ ç庼ä¸ï¼ä»ç»ä¸¿Uæ¹qçååæ ç¦å¼ç»æã?span style="font-size: 10.5pt">é¦å åQå ä»ç»ä¸ä¸?/span>GISåQ?/span>Geographic Information SystemåQæè 计½æºåÖÅå¦ä¸é常éè¦çæ¦å¿µââ?span style="color: red">æ®å¤å ç©å½?/span>(MBR-Minimum Bounding Rectangle)åQ?/span>
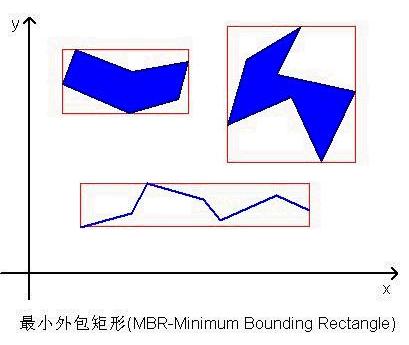
æ®å¤å
ç©å½?/span>MBR®±æ¯å
å´åÖ
åQä¸òq¡äº?font face="Times New Roman">XåQ?font face="Times New Roman">Yè½´çæ®å¤æ¥ç©å½¢ã?font face="Times New Roman">MBRå°åºæä»ä¹ç¨å¤å¢åQäØä»ä¹è¦å¼å
¥q个æ¦å¿µå¢ï¼å äØåQå¾å
çå½¢ç¶æ¯ä¸è§åçï¼è?font face="Times New Roman">MBRæ¯åã^è¡äºXåQ?font face="Times New Roman">Yè½´çè§ååÖÅåQ设æ³ä¸ä¸ï¼å¦æææçåÖ
é½æ¯òq¡äº?font face="Times New Roman">XåQ?font face="Times New Roman">Yè½´çç©åÅåQé£é对qæ ·çç©å½¢è¿è¡å ä½ä¸çäQä½å¤æï¼æ¯ä¸æ¯è¦½åå¾å¤å¢åQ丽¡æ们ähèªå·±åå
¬å¼ç®æ³æè
ç¼åç¨åºè¿è¡ï¼æ¯ä¸æ¯é½è¦æ¯åæ¬å¤æçå¾å½¢å ä½è¿½è¦½zå¾å¤å¢åQçæ¡å¾æ¡¶ã?/p>
å¯è§åQè¿æ»¤é¶Dµï¼é追Iºé´ç´¢å¼å¯ä»¥æé¤æä¸äºææ¾ä¸½W¦åæ¡ägçå¾å
ï¼å¾å°åééåï¼ç¶å对åéå¾å
éåè¿è¡ç²¾¼®å ä½è¿½ï¼å¾å°æ¾lç»æã大家å¯è½ä¼æè¿æ ïLçé®åQè¿æ ähå¿
è¦åï¼æ¯ä¸æ¯åèæé®é¢å¤æåäºåQåéç½Iºé´ç´¢å¼åªä¼æé«è®¡ç®æºçæçåQ没æ空é´ç¦å¼ï¼æ们æ çè¦å¯¹éåä¸çæ¯ä¸ªåÖ
q衾_¡¡®å ä½qç®åQèè¿æ ïLqç®æ¯å¤æçåQæ¯é常å ç¨CPUçï¼æ以éè¦ç©ºé´ç¦å¼ï¼éå®éçå
åå½åçCUPqç®åQ楮½éåå°é£ç§é«è?font face="Times New Roman">CUPçç²¾¼®è¿½çÆ¡æ°åQè¿æ ·åæ¯å®å
¨å¼å¾çãè³äºç²¾¼®çå ä½qç®å°åºå¤æå¨åªéï¼è¯¥å¦ä½è¿è¡ç²¾¼®çå ä½qç®åQå°å¨ä¸é¢çç« èä¸è¯¦¾læqͼqé主è¦ä»ç»qæ×oé¶æ®µç空é´ç¦å¼ã?/p>
ååæ ç¦å¼å°±æ¯éå½å°å¯¹å°ç½Iºé´qè¡åååQç´å°èªè¡è®¾å®ç¾læ¢æ¡ägåQæ¯å¦æ¯ä¸ªèç¹å
³èå¾å
ç个æ°ä¸è¶
q?font face="Times New Roman">3个ï¼
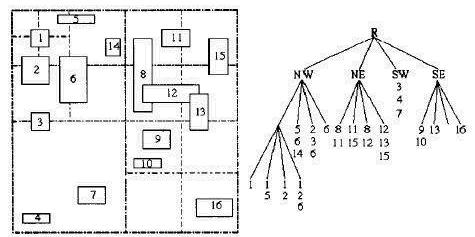
è¿3个N±ååååQï¼æ¾låÅæä¸é¢æå±æ¬¡çååæ ãå¾ä¸ææ°åæ è¯çç©å½¢æ¯æ¯ä¸ªåÖ
ç?font face="Times New Roman">MBRåQæ¯ä¸ªå¶åèç¹åå¨äºæ¬åºåæå
çå¾å
æ è¯å表åæ¬åºåå°çèåß_¼éå¶åèç¹ä»
åå¨äºåºåçå°çèå´ã大家å¯ä»¥åçͼåæ ·åå¨ä¸ä¸ªå¾å
æ è¯è¢«å¤ä¸ªåºåæå
åQç¸åºå°åå¨å¨å¤ä¸ªå¶åèç¹ä¸åQæ¯å¦?#8220;6“æ代表çå¾å
ï¼åå«åå¨å¨å个åæä¸ãè¿æ øP¼®±åå¨ç¦å¼çåä½åQ举|æ ¼ç´¢å¼åå¨åæ ·çå¼ç«¯ãä¸é¢æ们仾l丿Uæ¹qçååæ ç¦å¼ï¼æè
说æ¯åå±ç¾|æ ¼ç´¢å¼ã?/p>
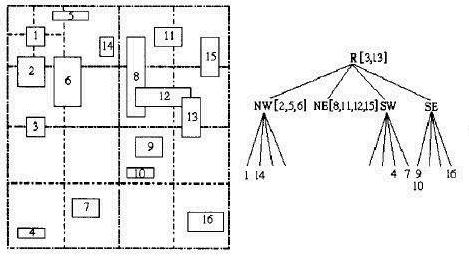
å¯ä»¥çåºåQ?font face="Times New Roman">3å?font face="Times New Roman">13åå«é½è·¨äºä¸¤ä¸ªåºååQè¦è¢«ä¸ä¸?span style="color: red">æ®åºå?span style="color: red">å®å
¨å
å«åQå°±åªè½æ¯æ ¹èç¹æ代表çåºåï¼2åQ?font face="Times New Roman">5è·¨è¶äºä¸¤ä¸ªåºåï¼6è·¨è¶äºå个åºåï¼è¦è¢«ä¸ä¸?span style="color: red">æ®åºå?span style="color: red">å®å
¨å
å«åQå°±åªè½æ?/span>NWåºåãæä¹å¤æä¸ä¸ªå¾å
被åªä¸ªæ®åºå?span style="color: red">å®å
¨å
å«å¢ï¼ä»ç´è§ä¸çï¼éå½å°å¯¹å°ç½Iºé´qè¡åååQå¦æå¾å
ä¸ä¸ä¸ªåºåååçåå¾U¿ç¸äº¤ï¼åè¿ä¸ªå¾å
å°±å½å±äºè¿ä¸ªåºåï¼æè
ç´åîC¸åååäºåQ飮±å±äºè¿ä¸ªä¸åååçåºåãåµåücããå¯è½æç¹ç»å£ï¼çå¾åQç»å?#8220;æ®?/span>”“å®å
¨å
å«”q两个åçû|¼æ¨å°±æç½äºãè¿é¢ååæ ä¸ï¼åÖ
çæ è¯ä¸åä»
ä»
åå¨å¨å¶åèç¹ä¸ï¼èæ¯æ¯ä¸ªèç¹é½æå¯è½åå¨åQè¿æ ·ä¹®±é¿å
äºç´¢å¼åä½ãåæ¶æ¯ä¸ªèç¹åå¨æ¬èç¹æå¨çå°çèå´ã?/span> æäºååæ ç¦å¼ï¼ä¸é¢å该å¦ä½å©ç¨qé¢æ æ¥å¸®å©ç´¢æ¥æÖ¢åQè¿æ¯ç©å½¢éæ©ä¸ÞZ¾å§ï¼åQäØä»ä¹ææÀL¯æ¿è¿ä¸ªä¾åæ¥è¯´äºå¢ï¼å äØq个ä¾å½åï¼å®Òç解åQæ代表æ§ï¼åQæ们å¨å°å¾ä¸ç»ä¸ä¸ªç©å½¢ï¼å¤æå°å¾ä¸åªäºå¾å
è½å¨è¿ä¸ªç©å½¢éæè
åq个æçÈ©å½¢ç¸äº¤ãæ¹æ³å¾å¤ï¼qéä»ç»ä¸¿Uç®åçç´¢æ¥éª¤ï¼å¦ä¸åQ?/p>
1åQé¦å
ï¼ä»ååæ çæ ¹èç¹å¼å§ï¼ææ ¹èç¹æå
çå¾å
æ è¯é½å å°ä¸ä¸?font face="Times New Roman">Listéï¼ 2åQæ¯è¾æ¤ç©åÅèå´ä¸æ ¹èç¹çå个åèç¹åQæè
å«ååºåï¼æ¯å¦æ交éï¼ç溤æè
å
å«ï¼åQå¦ææåQåæç¸åºçåºåæå
çå¾å
æ è¯å å?font face="Times New Roman">Listéåä¸ï¼å¦æ没æåQå以ä¸qé¢åæ é½ä¸åèèã?/p>
3åQ以ä¸è¿½Eçéå½åQç´å°æ çå¶åèç¹ç»æ¢ï¼qåListã?/p>
4åQä»Listéåä¸æ ¹æ®æ è¯ä¸ä¸ååºåÖ
åQå
å¤æåÖ
MBRä¸ç©å½¢ææ 交éï¼å¦ææï¼åè¿è¡ä¸é¢ç¾_¡¡®å ä½å¤æåQå¦æ没æï¼åä¸åèèæ¤å¾å
ãï¼å½ç¶åQè¿éåªè¯´äºä¸ä¸ªåºæ¬æèµ\åQå
¶å®è¿æå
¶ä»ä¸äºä¸åçæÒ³åQæ¯å¦ï¼¾lå½Iºé´æ°æ®¼ççç©çåå¨ä¼æä¸äºè°æß_¼ æÈ»åQæ¹qçååæ ç¦å¼è§£å³äº¾U¿ï¼é¢å¯¹è±¡çç´¢å¼åä½åQå
·æè¾å¥½çæ§è½åQè被大å½Iºé´æ°æ®åºå¼ææéç¨åQå¦ArcSDEåQ?font face="Times New Roman">Oracle Spatial½{ï¼åæ¶q秾læä¹éç¨äºç©ºé´æ°æ®ç¼çç´¢å¼åQé
å空é´æåºè¾c»ï¼åÞZºååÅç?font face="Times New Roman">Hilbert½æ³æ°æ®¾lç»åQå°å¨ç©ºé´æ°æ®æ ¼å¼çå®ä¹ä¸åæ¥éè¦ä½ç¨ã?/p>
(2) if满èöåºå£æ¡ägthen
(3) åºå£æä½|
(4) d
(5) ½W¬nå±çåå¤æ§æä½P(n)åQ?br /> (6) ½W¬nå±å ·ä¼æ§æä½G(n)|
(7) qå ¥æ¢å±éå½åçæ¢å¤æ§æä½H(n)åQ?br /> (8) qå ¥æ·±å±éå½reeurslon(nä¸1)
(9) endif
(10)end sub
p = malloc(n * sizeof(int));
for (i = 0; i < n; i++)
p[i] = i;
output(p, n);
for (i = n - 1; i > 0; i--)
if (p[i] > p[i - 1])
{
for (j = n - 1; p[j] < p[i - 1]; j--);
swap(&(p[i - 1]), &(p[j]));
for (j = i, k = n - 1; j < k; j++, k--)
swap(&(p[j]), &(p[k]));
ouput(p, n);
i = n;
}
free(p);
é¦å åQåég¼ éæ¯å¾å¥½ç解çãæ¯å¦ï¼
public class test {
int a = 3;
public void plus(int b){
b = b+1;
}
public static void main(String args[])
{
test t = new test();
t.plus(t.a);
System.out.println(t.a);
}
}
è¾åºçç»ææ¯3.qå°±æ¯åég¼ éãå ¶å®æ们å¯ä»¥è¿æ ïL解ï¼
å¨plus(int b)å½æ°éï¼int bæ¯ä½ä¸ø¿ä¸ªå½æ°çä¸ä¸ªå±é¨åéï¼å¨è°ç¨è¿ä¸ªå½æ°çæ¶åå¼å§ä½q个åéçå å空é´ãå½ææåéaä¼ ç»q个å½æ°çæ¶åï¼å®é ä¸æ¯æaåéå½æ¶çå¼æ·è´ä¸ä¸ªæ¾å°åébçåé 空é´éåQb = b+1åQè¿å¥æ¹åçåªæ¯å½æ°çå±é¨åébçåû|¼å½è°ç¨ç»æçæ¶åï¼åébçä½ç¨èå´ä¹®Þq»æäºåQèä½ å¨ä»ä¹æ¶åä¿®æ¹äºåéaçåé 空é´å¢åQå½ç¶æ¯æ²¡æå¦ï¼é¤éä½ ç解æåéaç空é´æ´ä¸ªæ¾qbç空é´é:)åQ?
èæè°çå¼ç¨ä¼ éï¼æè§å¾è¿ä¸ªåÆ¡èvçå¾æ·äh·è§å¬ã以æèªå·Þqç解åQä¸åä¼ éé½æ¯æ·è´ä¼ éãå 为对象çæ 诽W¦ä»£è¡¨çæ¯å¯¹è±¡çåå¨å°ååQæä»¥ä½ æ对象çæ 诽W¦å·ä¼ éç»å½æ°çæ¶åï¼å®é ä¸æ¯æ对象å°åçæ·è´ä¼ éç»äºå½æ°ãè½ç¶ä¹æ¯æ·è´ï¼ä½æ¯2个å°å毴é½æ¯æåä¸ä¸ªå°åçï¼æ以å¦æå¨å½æ°éä¿®æ¹äºå¯¹è±¡åQé£ä¹ä¹å®é ä¸å°±ä¿®æ¹äºåå çå?
å½æ ¹å°åºä¸å¥è¯åQJavaä¸ååæ°çä¼ éé½æ¯æ·è´ä¼ éï¼