http://www.aygfsteel.com/jungleford/archive/2005/04/02/2759.html
jungleford如是說
對于Java集合框架（Java Collections Framework，JCF），Java玩家大概都不會陌生，在C++里面相似的概念是標準模板庫（Standard Template Library，STL），主要是對一些數(shù)據(jù)結(jié)構(gòu)和相關(guān)算法的封裝?？紤]到這是一個Java初學者將會經(jīng)常接觸的工具，所以有了以下的一些文字。主要是參考了IBM developerWorks上的一篇教程，它可能解釋得更加清晰，這里算是濃縮了一下吧，真正的來龍去脈可以看看JDK文檔里的“The Collections Framework”，說明更為詳細。
問題的源頭
- 集合：對象的容器與數(shù)據(jù)結(jié)構(gòu)
回憶一下我們在程序設(shè)計里頭可能會面對一些什么，無非是兩類：基本類型和復合類型，后者常見的組織方式就是類。和基本類型不同，類對象通常是需要以動態(tài)方式分配的，譬如在內(nèi)存的堆空間里new一個對象，這個我們一寫OO的程序就必然會用到。同時我們面對的不僅僅是單個的基本類型或?qū)ο?，對多個這樣的數(shù)據(jù)我們通常采用的組織方式是什么？不錯，是數(shù)組，這是伴隨程序設(shè)計的一個古老概念。數(shù)組的優(yōu)點顯而易見，像根據(jù)下標檢索元素這樣的操作不費吹灰之力，但缺點也很明顯：空間固定而不能動態(tài)增長（像Java這樣的強類型語言對數(shù)組越界是及其敏感的），插入或刪除元素比較費勁。因此數(shù)組不是解決一切集合問題的方便工具。我們可能需要一些新的工具，研究這些工具常常就是研究數(shù)據(jù)結(jié)構(gòu)，特別的，數(shù)組本身就是一種線性有序的數(shù)據(jù)結(jié)構(gòu)。
數(shù)據(jù)結(jié)構(gòu)的數(shù)學基礎(chǔ)是集合論，為什么這么說呢？上面說過，現(xiàn)在我們要研究的不是單個的基本類型或?qū)ο?，多個對象的整體不就是集合嗎？從OO的角度上看，集合也是一種對象，但它是一種特殊的對象：對象的容器（注意，我們這里沒有繼續(xù)討論基本類型的集合，因為基本類型和存儲分配方式與對象有著本質(zhì)的差別）。集合論的一個根本問題就是：給定一個元素，集合必須能夠回答該元素是或者不是屬于這個集合。還有一個問題也很重要，就是：如果元素是屬于一個集合，那該元素在集合中的地位應該是唯一的，或者說它是唯一確定的。當然還有其它問題，譬如查找、遍歷、排序等等，這和具體的集合類型相關(guān)，后面將會講到。
談到集合的類型，我們在高中所學的集合概念是其中的一種，叫做“無序集”，也就是說集合的各個元素都是平等的，沒有先后的區(qū)別，于是在無序集當中就決不允許出現(xiàn)一模一樣的元素，否則當取到這個元素的時候就不知道應該取哪一個，這就違反了上面的“唯一確定”原則。
等到我們上了大學，開始知道了另一種集合類型，叫做“有序集”（或者叫“線性表”，區(qū)別于以后碰到的像“樹”，“圖”這樣的非線性的數(shù)據(jù)結(jié)構(gòu)），如果是計算機專業(yè)的，大概學過離散數(shù)學當中的“代數(shù)結(jié)構(gòu)”，那你就更清楚的知道，“有序集”其實是一種“二元關(guān)系”，確切的說是“偏序關(guān)系”，它是可以包含相同元素的，因為兩個的相同元素的“序號”可以不同，這樣根據(jù)“序號”仍可以“唯一確定”一個元素，數(shù)組就是一種有序集，有序集的另一個特點就是任意兩個元素可以確定他們的順序。
無序集，有序集，難道還有第三種可能？呵呵，它還是出現(xiàn)在我們的高中代數(shù)課本里，叫做“映射”。映射也是集合？其實自從康托爾以來，集合論就認為“萬物皆集合”（但也就是這個斷言導致了集合論以后的尷尬境地，有興趣可以看看羅素或哥德爾的一些結(jié)論，或google“集合論 悖論”）。映射其實是一種“元素對”的集合，就像f(a)=b, f(c)=d, ...等效于集合（無序集）{(a, b), (c, d), ...}，在“映射”中可以看作是(原象, 象)的集合，換一種說法就是(關(guān)鍵字key, 值value)的集合。所以我們可以在笛卡兒正交坐標平面上畫出漂亮的函數(shù)圖像，因為在集合論看來，函數(shù)（映射）就是二維平面上的一個個點，明白了？這樣一來上面的“有序集”也好理解了，偏序關(guān)系a>b>c>d>...（不知道“偏序關(guān)系”就把它們看作是數(shù)組x[1]=a, x[2]=b, x[3]=c, x[4]=d ...好了）等效于無序集{(1, a), (2, b), (3, c), (4, d), ...}，于是乎，所有的集合都等效于無序集！所以高中只教了我們一種集合，呵呵……
JCF的全家福
好啦好啦，這些我們都知道，又不是在上數(shù)學課，說了這么多廢話，怎么還沒扯到正題上來？JCF的影子我還沒看見呢！列位看官別急，這就給您道來。其實上面的概念對理解JCF非常重要。
JCF是個頗有點規(guī)模的家族，看看它的類層次關(guān)系圖就知道了，下面這張圖（圖1）摘自著名的Thinking in Java：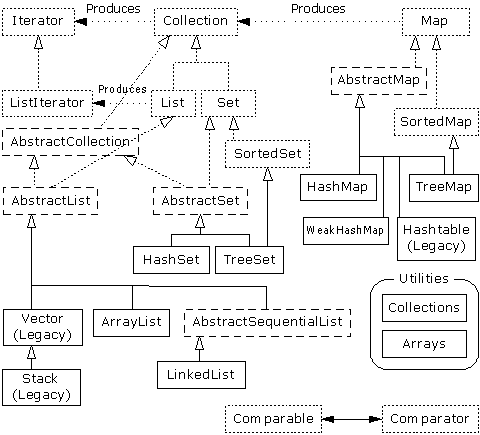
圖1 JCF層次結(jié)構(gòu)
哇，這么多接口和類，真有點讓人無從下手的感覺。其實我們真正需要記住的只是這么一個超超easy的結(jié)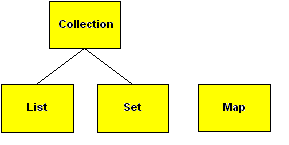構(gòu)（圖2）：
圖2
這張圖看起來舒服多了吧？但它又能說明什么問題呢？它怎么就能夠把握整個JCF呢？我們把Collection接口置于最頂上，意思是想說：Collection其實是整個JCF家族中的“祖宗”，幾乎所有的JCF成員都源自該接口，或者和它有密切的關(guān)系，Collection提供關(guān)于集合的一些通用操作的接口，包括插入（add()方法）、刪除（remove()方法）、判斷一個元素是不是其成員（contains()方法）、遍歷（iterator()方法）等等。注意了，前面的“廢話”在這里將得到體現(xiàn)：Set接口體現(xiàn)的是“無序集”的概念，它是不允許有重復元素出現(xiàn)的；List接口代表“有序集”；而Map接口則是“映射”（在早期的Java版本中并不叫Map，我們在后面會看到），其實Map.Entry接口就是代表一個“元素對”我們可以通過Map的entrySet()方法得到這樣一個由“元素對”組成的Set對象。我們注意到Set和List都是從“祖宗”Collection派生的，而Map不是，畢竟對一對元素的操作與對單個元素的操作還是有區(qū)別的，但是如果你仔細對照一下Collection和Map的源代碼，以及它們的直接后代AbstractCollection和AbstractMap的源代碼，你將會發(fā)現(xiàn)很多相似的地方，所以我們?nèi)匀豢梢园袽ap看成是和Collection有著血緣關(guān)系的接口，而和Set，List一起處于并列的位置。
有了“無序集”，“有序集”和“映射”，我們就可以定義各種各樣的抽象數(shù)據(jù)結(jié)構(gòu)了，譬如圖1所示的向量，鏈表，堆棧，哈希表，平衡二叉樹等。但我們需要記住的，僅僅是圖2，置于其它的成員，在用到的時候查一下API手冊不就行了？不過一般初學者還是比較容易用到一些類，像Vector、ArrayList、HashMap，我在這里列了一張表，顯示了常見的JCF成員及其關(guān)系：
可能有的概念您還不是太了解，譬如什么叫“歷史集合”，Hashtable、HashMap、TreeMap三者之間有什么區(qū)別和聯(lián)系，怎樣實現(xiàn)對一個特定集合的快速遍歷、元素查找或者排序，沒關(guān)系，我們在下面將逐一進行研究。
細節(jié)考慮：目標與效率
有了JCF的層次還不夠，重要的是對集合所容納的對象的具體操作，以前我們學數(shù)據(jù)結(jié)構(gòu)的時候可能老師總會讓你計算一個算法的時間復雜度，可能你會對這個O(f(n))很不耐煩，但事實上算法效率是一個重要的因素。
對集合的有兩個主要的應用：我需要知道集合有哪些元素；根據(jù)條件找到一個特定的元素。在算法上通常稱為“遍歷”和“查找”。不要以為我們生活中不常用哦！譬如CCTV的“幸運52”里面，李詠讓參賽者報出一款PDA的準確價位，他會怎么做？“2000”“高了”“1000”“低了”“1500”“低了”……直到答對為止?？赡苡泻芏嗳硕紩x擇這個策略，無論他是不是計算機專業(yè)出身的，也不知道他是不是了解“數(shù)據(jù)結(jié)構(gòu)”和“折半查找”，更不用說他是不是知道還有比在無初始代價下O(log n)的時間復雜度更快的算法了，但我們經(jīng)常會自然而然地用這樣的方法，這和一個人的行業(yè)無關(guān)，除非這個人的rp超強，呵呵……
又講了一堆題外話了，遍歷和修改似乎是一對矛盾，一個可以高效率插入刪除元素的數(shù)據(jù)結(jié)構(gòu)通常遍歷的性能并不是最優(yōu)。于是JCF在這里根據(jù)用戶的目標實現(xiàn)了兩種定制的數(shù)據(jù)結(jié)構(gòu)：哈希表（包括HashSet和HashMap）和平衡二叉樹（包括TreeSet和TreeMap）。由于可排序性是一種獨特的要求，所以引入了SortedSet和SortedMap，它們分別是AbstractSet和AbstractMap的子接口，而TreeSet和TreeMap又分別是他們的一種實現(xiàn)。熟悉數(shù)據(jù)結(jié)構(gòu)的人可能比較了解，哈希表在進行插入、刪除、查找這樣的操作是很快的，其時間復雜度是常數(shù)級O(1)；平衡二叉樹雖然插入、刪除操作比較麻煩（需要O(log n)的代價），但進行遍歷和排序卻很快。選擇完全在于用戶的側(cè)重點，但由于類型轉(zhuǎn)換的方便性，通常我們用哈希表構(gòu)造一個集合以后，再把它轉(zhuǎn)換成相應的樹集進行遍歷，以獲得較好的效果。
Set set1 = new HashSet();
set1.add(elem1);// 通過插入元素構(gòu)造集合
set1.add(elem2);
set1.add(elem3);
Set set2 = new TreeSet(set);
Iterator all = set2.iterator();
while (all.hasNext())
{// 遍歷集合
all.next();
...
} |
2. 歷史實現(xiàn) vs. 新實現(xiàn)
歷史實現(xiàn)（Legacy Implementations）是JCF的一個術(shù)語，準確的意義不是很清楚，但大致可以認為在Java 2（JDK 1.2）出現(xiàn)以前的老版本中JCF的一個雛形框架。在Java 2以后，JCF才開始完善健壯起來，新實現(xiàn)中出現(xiàn)了一些新的類用于替代老版本中的成員，但由于種種原因，老版本中很多類都代表了傳統(tǒng)數(shù)據(jù)結(jié)構(gòu)的精髓部分，以及一些安全原因，所以仍然被我們使用著。
Enumeration vs. Iterator Enumeration是一個傳統(tǒng)的集合遍歷工具，在新的JCF中使用的是Iterator，Iterator同樣具有遍歷功能，還包含一個remove()方法來刪除當前得到的元素。
Dictionary vs. Map Dictionary是一個現(xiàn)在已經(jīng)被標記為deprecated的類，實現(xiàn)了老版本中的映射功能，現(xiàn)在已經(jīng)完全被Map取代。它們的區(qū)別是：Dictionary中key和value不能為null，但Map卻允許空的關(guān)鍵字和值，這一點直接影響到它們的后代：Hashtable和HashMap。
Vector vs. ArrayList Vector和ArrayList是數(shù)組在JCF中的體現(xiàn)，還記得前面講過的數(shù)組的缺點么？Vector和ArrayList就是一種可以動態(tài)增長的數(shù)組。Vector是歷史實現(xiàn)，它和ArrayList的主要區(qū)別在于，Vector是同步集合（或者說是線程安全的），但ArrayList并不是同步的，由于同步需要花一定的代價，所以ArrayList看起來要比Vector的存取訪問效率更高。關(guān)于同步我們下面還將要談到。
Hashtable vs. HashMap Hashtable是Dictionary的子類，屬于歷史實現(xiàn)，而HashMap是Map的子類，是新實現(xiàn)。它們的區(qū)別除了上面所說的key和value是否可以為空之外，也有同步的差別，Hashtable是同步的，但HashMap不是。HashMap的一個經(jīng)典的例子就是JSP的內(nèi)置對象session。不過不要因為Hashtable是“老前輩”而瞧不起它哦，它的一個著名的子類Properties我們可是經(jīng)常會用到的。
從上面的描述中我們似乎可以得出這么一個印象：歷史實現(xiàn)好像都是同步的，但新實現(xiàn)中卻沒有。需要同步操作的理由是，可能存在多個線程對同一個集合進行操作的情況：譬如一個線程正在對某集合進行遍歷，但與此同時，另一個線程又在對該集合進行插入或刪除，那么第一個線程的遍歷結(jié)果將是不可預測的，對于同步集合，它將會拋出一個ConcurrentModificationException異常，JCF把這種機制成為“fail-fast”。我們對比一下Vector和ArrayList的源代碼就可以發(fā)現(xiàn)Vector的很多方法都是有synchronized關(guān)鍵字修飾的，但ArrayList沒有。
在圖1中右下角落里有兩個類叫做Collections（注意，不是Collection?。┖虯rrays，這是JCF里面功能強大的工具，但初學者往往會忽視。按JCF文檔的說法，這兩個類提供了封裝器實現(xiàn)（Wrapper Implementations）、數(shù)據(jù)結(jié)構(gòu)算法和數(shù)組相關(guān)的應用。
想必大家不會忘記上面談到的“折半查找”、“排序”等經(jīng)典算法吧，Collections類提供了豐富的靜態(tài)方法幫助我們輕松完成這些在數(shù)據(jù)結(jié)構(gòu)課上煩人的工作：
binarySearch：折半查找。
sort：排序，這里是一種類似于快速排序的方法，效率仍然是O(n * log n)，但卻是一種穩(wěn)定的排序方法。
reverse：將線性表進行逆序操作，這個可是從前數(shù)據(jù)結(jié)構(gòu)的經(jīng)典考題哦！
rotate：以某個元素為軸心將線性表“旋轉(zhuǎn)”——哇，這個功能太酷了！
swap：交換一個線性表中兩個元素的位置。
……
Collections還有一個重要功能就是“封裝器”（Wrapper），它提供了一些方法可以把一個集合轉(zhuǎn)換成一個特殊的集合：
unmodifiableXXX：轉(zhuǎn)換成只讀集合，這里XXX代表六種基本集合接口：Collection、List、Map、Set、SortedMap和SortedSet。如果你對只讀集合進行插入刪除操作，將會拋出UnsupportedOperationException異常。
synchronizedXXX：轉(zhuǎn)換成同步集合。
singleton：創(chuàng)建一個僅有一個元素的集合，這里singleton生成的是單元素Set，singletonList和singletonMap分別生成單元素的List和Map。
空集：由Collections的靜態(tài)屬性EMPTY_SET、EMPTY_LIST和EMPTY_MAP表示。
此外，我們知道把集合轉(zhuǎn)換成對象數(shù)組可以用Collection的toArray()方法，我們也可以方便地把一個對象數(shù)組轉(zhuǎn)換成一個線性表（可不要告訴我你是一個一個地add哦）：Arrays.asList()。
目前我們了解的JCF的一個重要特征是：所有加入到集合當中的對象都將在表面上失去它們自己的特性，而看上去僅僅只是一個Object對象而已，除非你把它強制類型轉(zhuǎn)換成它們原來的對象。這一點很自然，集合嘛，對象的容器，它容納的是各種各樣的對象，而不僅僅是某種特定類型的對象。J2SE 5.0出現(xiàn)以后，JCF開始引入泛型的特性，譬如我們經(jīng)常碰到這樣的應用，就是把集合轉(zhuǎn)換成特定的數(shù)組，雖然Collection有toArray()的方法，但可惜的是，這個數(shù)組的所有元素都是Object類型的，我們通常的做法是用一個for循環(huán)把數(shù)組的每個元素都進行強制類型轉(zhuǎn)換，雖然可行，但看上去很笨拙，如果有了泛型，我們就可以預先指定要得到的類型，然后一次toArray就可以得到我們期望的數(shù)組，里面的元素全部都是指定類型了。慚愧的是，我對5.0還不是太了解，具體可以參考J2SE 5.0的JCF文檔。
小結(jié)
我這里走馬觀花一樣把JCF的一些主要概念羅嗦了一下，Java的老手們可能比較厭煩，新手們可能更覺得像回顧了一下高中的數(shù)學課和大學的數(shù)據(jù)結(jié)構(gòu)，呵呵。這只是一個小小的例子，可見基礎(chǔ)知識對現(xiàn)實當中的應用還是蠻有指導意義的。大師們看數(shù)學，覺得那是很唯美很藝術(shù)的一樣東西，西方一直都把數(shù)學區(qū)別于其它自然科學，而認為它更靠近于哲學，像我等這樣整天還在為找工作煩得要死的俗人還是沒法入道啊，sigh……
參考資料