被代理class name(包名和類名) + "$$" +
使用cglib處理的class name(只有類名,不包含包名) +"ByCGLIB" + "$$" +
key的hashcode(接下來會對key有一個詳細的分析) +
序列號
下面是上面規則的示例:
aop.target.HelloImpl$$EnhancerByCGLIB$$494b5b61
aop.target.HelloImpl$$EnhancerByCGLIB$$494b5b61_2
aop.target.HelloImpl$$EnhancerByCGLIB$$494b5b61_3 閱讀全文
]]>
]]>
]]>
只需要在特定目錄添加一個文件:jaxp.properties
內容如下
javax.xml.parsers.DocumentBuilderFactory=com.sun.org.apache.xerces.internal.jaxp.DocumentBuilderFactoryImpl
javax.xml.parsers.SAXParserFactory=com.sun.org.apache.xerces.internal.jaxp.SAXParserFactoryImpl
如果是Bea/jrockit可以添加到如下類似目錄
D:\bea\jrockit_160_05\jre\lib
-Djavax.xml.parsers.DocumentBuilderFactory=com.sun.org.apache.xerces.internal.jaxp.DocumentBuilderFactoryImpl
-Djavax.xml.parsers.SAXParserFactory=com.sun.org.apache.xerces.internal.jaxp.SAXParserFactoryImpl
]]>
一、靜態部署
靜態部署指的是我們在服務器啟動之前部署我們的程序,只有當服務器啟動之后,我們的Web應用程序才能訪問。以下3中方式都可以部署:
1、將PetWeb目錄拷貝到$CATALINA_HOME\webapps下,然后啟動服務器就可以了。這種方式比較簡單,但是web應用程序必須在webapps目錄下。訪問地址如下:
http://localhost:8080/PetWeb/
2、這種方式可以不必將PetWeb目錄拷貝到webapps下,直接在F:\部署。方法如下,更改$CATALINA_HOME\conf\server.xml文件,在<host>標簽內添加<Context>標簽,內容如下:
<Context docBase="F:/PetWeb" reloadable="false" path="/Pet"/>
其中reloadable="false"表示當應用程序中的內容發生更改之后服務器不會自動加載,這個屬性在開發階段通常都設為true,方便開發,在發布階段應該設置為false,提高應用程序的訪問速度。docBase為路徑,可以使用絕對路徑,也可以使用相對路徑,相對路徑相對于webapps。path屬性的值是訪問時的根地址。訪問地址如下:http://localhost:8080/Pet/
3、這種方式和第二種方式差不多,但是不是在Server.xml文件中添加Context標簽,而是在$CATALINA_HOME\conf\Catalina\localhost中添加一個xml文件,如Pet.xml,內容如下:
<Context docBase="F:/PetWeb" reloadable="false" />大家可能發現和第二種方式差不多,但是缺少了path屬性,這種方式服務器會使用.xml的名字作為path屬性的值。訪問地址如下:http://localhost:8080/Pet/
我們剛才是將PetWeb文件夾部署在了服務器中,我們知道可以將Web應用程序的內容打成.war包,然后在部署在服務器上。打包請參考如下步驟:
1、打開命令提示符(Start-->Run-->cmd)
2、設置jdk環境變量(如果我教過的學生不會配置,以后別說孫老師教過你)
3、在命令提示符中進入F:\PetWeb文件后,鍵入如下命令:
jar ..\Pet.war *.* 這樣在F:\下應該有Pet.war文件。其中..表示當前目錄的父目錄。
部署Pet.war文件非常簡單,將剛才有docBase="F:\PetWeb"更改為docBase="F:\Pet.war"或者直接將其拷貝到webapps下也可以。重新啟動服務器就可以將Pet.war部署為一個Web應用程序了。如果你夠細心的話你會發現,服務器將Pet.war文件解開,并且在webapps下面又生成了一個Pet文件夾,然后把Pet.war的內容拷貝到里面去了。我們可以通過以下方式取消自動解壓縮,配置方式如下:
<Context docBase="F:/PetWeb" reloadable="false" unpackWAR="false"/>
二、動態部署
動態部署是指可以在服務器啟動之后部署web應用程序,而不用重新啟動服務器。動態部署要用到服務器提供的manager.war文件,如果在$CATALINA_HOME\webapps\下沒有該文件,你必須去重新下載tomcat,否則不能完成以下的功能。要想使用該管理程序必須首先編輯$CATALINA_HOME\conf\tomcat-users.xml文件,內容如下:關于這個文件的更多內容,請參考Java Web應用程序的安全模型二
<tomcat-users>
<role rolename="tomcat"/>
<role rolename="role1"/>
<role rolename="manager"/>
<user username="coresun" password="coresun" roles="manager"/>
<user username="tomcat" password="tomcat" roles="tomcat"/>
<user username="both" password="tomcat" roles="tomcat,role1"/>
<user username="role1" password="tomcat" roles="role1"/>
</tomcat-users>
然后在瀏覽器中鍵入如下地址:
http://localhost:8080/應該看到一個漂亮的加菲貓了吧。點擊左邊的Tomcat Manager鏈接,提示輸入用戶名和密碼,本文都是coresun,然后可以看到以下頁面:

在Context Path(option):中輸入/Pet
XML Configration file URL中要指定一個.xml文件,比如我們在F:\下建立一個Pet.xml文件,內容如下:
<Context reloadable="false" />docBase不用寫了,因為在下一個文本框中填入。或者更簡單點,這個文本框什么都不填。
在WAR or Directory URL:中鍵入F:\PetWet或者F:\Pet.war都可以,然后點擊Deploy按鈕,看看上面是不是已經看到了你web應用程序,名字就是你Context Path(option):中的名字。
如果你部署.war文件還有更加簡單的方式,下面還有個Select WAR file uploae點擊瀏覽選擇.war文件,然后點擊Deploy也可以。
]]>
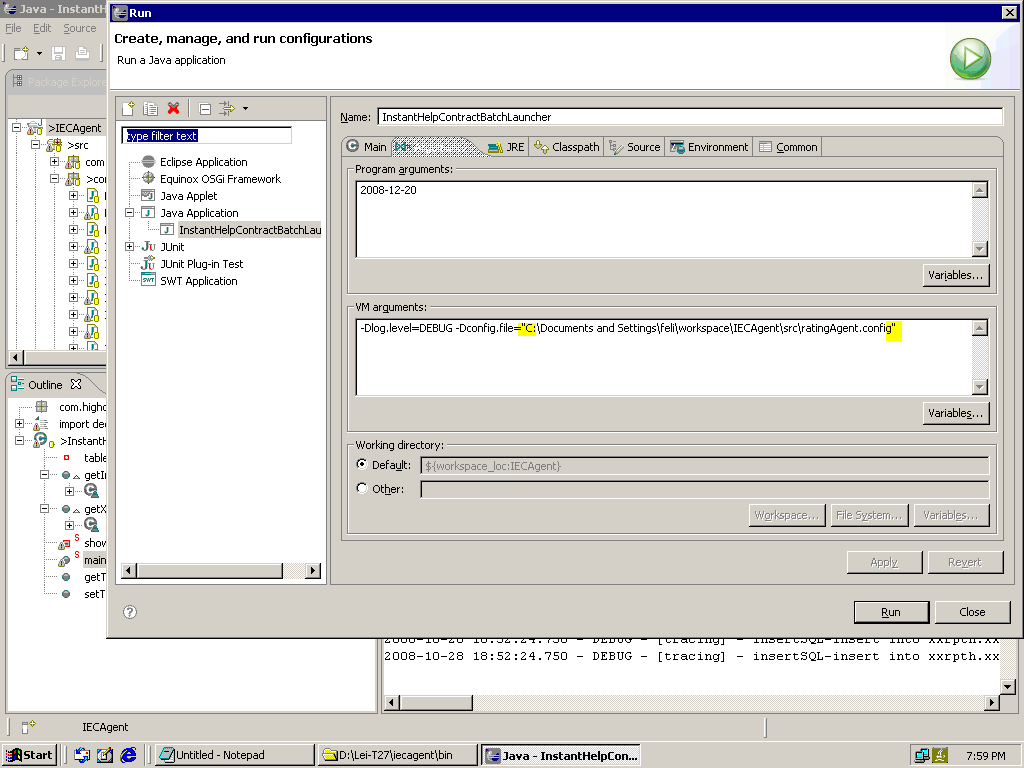
往Eclipse中輸入系統變量,run -> run..->arguments--> vm arguments.
Eg: -Dlog.level=DEBUG -Dconfig.file="C:\Documents and Settings\feli\workspace\IECAgent\src\ratingAgent.config"
有一點要注意的就是如果參數中有空格,要用引號括起來。
]]>
經過查找發現以前之所以可以,是因為剛好對應的工程是Maven得到的Eclispe工程,而Eclipse已經對Java文件編繹過了,并且默認的class輸出目錄是target/classes.而Maven運行mvn:compile也是把class輸出到此目錄.
所以打包前不必運行mvn:compile,但是如果不是Eclipse工程,或者是Eclipse沒有把Class輸出到target/classes,直接打WAR包,得到的包是不完整的,沒有class的.
]]>
<%@ page contentType="application/msword;charset=utf8" %>
<!-- 以上這行設定本網頁為Word格式的網頁 -->
<%
//response.setHeader("Content-disposition","inline; filename=test1.doc"); //線上瀏覽方式,用IE打開
response.setHeader("Content-disposition","attachment; filename=test1.doc");//下載方式,下載,不用瀏覽器打開
//以上這行設定傳送到前端瀏覽器時的檔名為test1.doc
//就是靠這一行,讓前端瀏覽器以為接收到一個word檔
//來源:http://www.xfuse.cn
%>
測試 http://www.xfuse.cn
]]>
log4j本來設置了要打印行號與文件名的,結果有的能打印出來,有的卻是亂碼,查了些文檔之后才發現,原來打印問題是因為編繹時沒有編繹進去調試信息,所以沒辦法打印.
但是我用的是Ant,如果在Ant編繹時,編繹進去調試信息呢,參考下面配置.
<javac srcdir="src" destdir="bin" debug="true" classpathref="accrual.path" >
首發于 http://blog.xfuse.cn
參考文檔
http://ant.apache.org/manual/CoreTasks/javac.html
Log4j配置
log4j.appender.C1.layout.ConversionPattern=%F(%L)-- %-4r %-5p [%t] %37c %3x - %m%n
如果是用JAVAC編繹,那么直接加參數-g就可以了.
用法:javac <選項> <源文件>
其中,可能的選項包括:
-g 生成所有調試信息
-g:none 不生成任何調試信息
-g:{lines,vars,source} 只生成某些調試信息
-nowarn 不生成任何警告
]]>
目標服務器:AJAX真實想想訪問的網址所在的服務器。
我遇到的問題就是:代理服務器通過HTTPS訪問目標服務器,但是目標服務器的證書出于一些原因并不被信任。
關鍵字:Ajax ,JavaScript, Coldfusion, HTTPS, cfhttp 閱讀全文
]]>
]]>
這樣是不是有可能兩個并行事務,同時讀取一個數據,然后再同時修改,先后提交事務。這樣就會有一個事務丟失其修改,不知道我理解的對不對。
?
]]>
]]>
大家可以親自體會一下。不過要有Web容器才行,實在沒有Web容器,用網絡鄰居也行。 閱讀全文
]]>
經過切換不同的關鍵字,我最后找到了正確的配置。 閱讀全文
]]>
??????在Tomcat下開發一些項目時,不可避免的會用到針對Tomcat的插件來進行調試,目前我接觸到的插件有如下三種,雖然它們都能對工程進行調試,它在一些其它功能上面卻有其區別
????? Myeclipse:這個是最強大的Eclipse插件,差不多什么都有,是一個一站式的解決插件。
????? WTP(Web Tools Platform):是由Eclipse自己開發的插件。
????? TomcatPlugin(sysdeo):最老牌的Tomcat插件,也是最好用的。
?
- Myeclipse插件對Tomcat的支持看起來應該是最好的,特點是熱部署。不管是對Servlet的修改,還是對web.xml的修改都可以。卻可以做到,哪個變了,就加載哪個。它可以很方便的把你的工程直接發布到Tomcat中去,或者是以war的形式發布過去。
- WTP(Web Tools Platform)
:相對MyEclipse于,WTP則實現了部署的透明化,Myeclipse在啟動Tomcat后,要你通過myEclipse把工程部署到Tomcat下,它會對你的Tomcat目錄下添加一些文件。但是WTP則對你的Tomcat不會有任何修改。
但我也發現了使用WTP 部署Web工程時的一個問題,對web.xml文件的修改不會自動的被重新加載,但更改Servlet會重新加載Servlet,并且同時重新加載web.xml。
也就是你想重新加載web.xml,你只有佯裝修改一個Servlet,才能觸發重新加載web.xml。不知道以后的版本會不會修改這點。 - TomcatPlugin(sysdeo):最老牌的tomcat插件了,相對來說在Tomcat調試領域也是最好用的了,不過它有點與WTP一樣,無法自動加載web.xml變化。但它也有它的絕招,是另外兩個插件不能比的。它有兩種支持調試的方式:
- 建立Tomcat工程,這時可以使用熱部署,tomcatPlugin(sysdeo)由于它并不真正的部署工程,使用TomcatPlugin(sysdeo)添加一個工程時,實際上在Tomcat\conf\Catalina\localhost目錄下添加了一個文件,當Tomcat啟動時就會加載這個工程,這時當然也可以調試。
- 另外一種支持調試的功能是其它兩個插件沒有的,比如你的工程是通過ANT布置到Tomcat下去的,你的目錄結構無法滿足WTP與Myeclipse的要求,這時你沒有辦法來使用這兩個插件來進行調度,但是使用TomcatPlugin卻可以。你只要在設置window->preferences->tomcat->soure path即可。
個人Blog:? http://www.aygfsteel.com/itspy
插件的適應環境:
???如果沒有特別的原因,應該盡量選擇TomcatPlugin(sysdeo)。
- 如果是一個全新的項目,上級完全放權了,你可以使用myEclipse與WTP,因為它能實現熱部署,調度修改代碼十分方便。但它們相對Tomcat來說,一個是侵入式的,一個卻是無侵入的。你可以針對這個特點來在兩者之間進行選擇。
- 如果是一個已經有一定歷史積累的工程,或者是無法對目錄結構進行控制的工作,這時推薦使用使用TomcatPlugin(sysdeo)。
因為myEclipse與WTP對工程對目錄結構都有一定的要求,因為它們要把工程部署到Tomcat上去,所以對工程目錄結構上都有自己的要求。比如在哪放置WEB-INFO,在哪個目錄放置源文件,并且兩個插件之間的工程無法形成兼容與共享。
但是TomcatPlugin(sysdeo)只是充當一個外掛來啟動Tomcat,并把指定的源代碼與Tomcat里面運行的項目關聯起來,進行調試。所以它對目錄結構沒有要求,比較適應于無法對目錄結構進行控制的項目,一個普通的Java工程即可以。
?個人Blog:? http://www.aygfsteel.com/itspy
]]>
??? private UserDao dao = null;
??? private RoleDao rdao = null;
???
??? public void setUserDao(UserDao dao) {
??????? this.dao = dao;
??? }
???
??? public void setRoleDao(RoleDao rdao) {
??????? this.rdao = rdao;
??? }
通過架構,這兩個Dao類都進行了自動裝載,后來的使用中,我才發現,所有類似的屬性都可以實現自動裝載.
?
?
這我就奇怪了,如果這些類是在Spring的ApplicationContext中設置的,我還知道,Spring提供了很多途徑來解決自動裝載問題.但是這些單元測試的類,都是由它們來管理生成ApplicationContext的,怎么也實現了自動裝載?
經常查看源碼,才知道原來是Appfuse架構中對DAO進行單元測試的類有一個共同的父類AbstractDependencyInjectionSpringContextTests,這個父類得到生成的ApplicationContext,會檢查自己有沒有一些屬性要實現自動裝載的,如果有就到ApplicationContext中去找,找到了就把自己子類的屬性實現自動裝載.
?
最核心的代碼是:AbstractDependencyInjectionSpringContextTests中有如下方法
?private void injectDependencies() throws Exception {
? if (isPopulateProtectedVariables()) {
?? if (this.managedVariableNames == null) {
??? initManagedVariableNames();
?? }
?? populateProtectedVariables();
? }
? else if (getAutowireMode() != AUTOWIRE_NO) {
?? this.applicationContext.getBeanFactory().autowireBeanProperties(
??? this, getAutowireMode(), isDependencyCheck());
? }
?}
?
?AbstractSingleSpringContextTests類中定義了下面的方法,這個方法實現了Junit的類TestCase定義的方法,這個方法會在每個方法之前運行。
? ?protected final void setUp() throws Exception {
??this.applicationContext = getContext(contextKey());//這個contextKey方法會調用BaseDaoTestCase中定義的getConfigLocations方法
??prepareTestInstance();
??onSetUp();
?}
]]>
Appfuse的登錄,權限控制都是通過Acegi來實現的,通過網上查找,看資料先后找到了兩個方法,和大家分享一下。 閱讀全文
]]>
]]>
只要在web.xml設置監聽器:org.springframework.web.context.ContextLoaderListener
并且配置一下如下參考
/WEB-INF/dataAccessContext-local.xml /WEB-INF/applicationContext.xml
但是內部細節是如何運作的呢? 閱讀全文
]]>
更奇怪的是在JAVA與C中它的表現還不一樣,剛好相反。 閱讀全文
]]>
]]>
得到String的大小,要用length方法
得到集合(比如List,Set)的大小,要使用size方法。
難道這沒有給你帶來不便嗎? 閱讀全文
]]>
現分別寫了兩塊代碼證明如下,至于為什么會有如此原因,我也不明白,希望有能懂C++與JAVA的人能出來講解一下。 閱讀全文
]]>
在Java中有一個動態代理技術,主要通過Proxy,InvocationHandler和Method,這三個類(接口)來實現.但是有如下一個問題不太明白,希望高手解惑.
我查看了幾個例子,它們實現InvocationHandler這個接口時,都通過構造函數傳遞進去了,實際被代理的對象,然后在實現的方法中通過method.invoke(obj,args);obj為構造函數傳遞進來的對象.
比如下面的例子:
public class Handler implements InvocationHandler {
?MethodInterface delegate;
?public Handler(MethodInterface delegate) {
??this.delegate = delegate;
?}
?public Object invoke(Object proxy, Method method, Object[] args)
???throws Throwable {
??if (method.getName().equals("say")) {
???System.out.print("I have get it");
??}
??return method.invoke(this.delegate, args);?
?}
}
函數invoke()傳遞進去的第一個參數proxy就沒有被使用到,但同樣實現了動態代理的效果,后面參考文獻中的例子也是的,難道是這第一個參數就是多余的,如果是這樣的話,就是Sun設置失誤了 ^__^.
sun的文檔是這樣解釋這個參數的:proxy - the proxy instance that the method was invoked on.但這個參數有什么用的,如果不傳遞他進來,會有什么不便呢.
有沒有人能明白這是怎么回事,或者是寫個示例代碼,講講這個第一個參數是干嘛用的?
?
?
注:附兩個完整的動態代理的例子
http://blog.csdn.net/hsyj_0001/archive/2006/04/02/647488.aspx
http://www.java2s.com/Code/Java/Development-Class/Demonstratesadynamicproxy.htm
]]>
?有一根27厘米的細木桿,在第3厘米、7厘米、11厘米、17厘米、23厘米這五個位置上各有一只螞蟻。 木桿很細,不能同時通過一只螞蟻。開始 時,螞蟻的頭朝左還是朝右是任意的,它們只會朝前走或調頭, 但不會后退。當任意兩只螞蟻碰頭時,兩只螞蟻會同時調頭朝反方向走。假設螞蟻們每秒鐘可以走一厘米的距離。 編寫程序,求所有螞蟻都離開木桿 的最小時間和最大時間。
看了這個題目之后,突然很感興趣,今天搞了半天把它做出來了,大概花了1個半小時.大公司的題目真是考人.反正都已經用算法實現了,我就不多說了,大家看代碼吧.代碼里面注釋我也盡量全寫了.一共有兩個類,一個是Ant的模型,一個是控制類.原代碼,大家可以在這取得:
http://www.aygfsteel.com/Files/itspy/baidu.rar
//////////////////////////////////////
/*百度面試題
?* 有一根27厘米的細木桿,在第3厘米、7厘米、11厘米、17厘米、23厘米這五個位置上各有一只螞蟻。
?* 木桿很細,不能同時通過一只螞蟻。開始 時,螞蟻的頭朝左還是朝右是任意的,它們只會朝前走或調頭,
?* 但不會后退。當任意兩只螞蟻碰頭時,兩只螞蟻會同時調頭朝反方向走。假設螞蟻們每秒鐘可以走一厘米的距離。
?* 編寫程序,求所有螞蟻都離開木桿 的最小時間和最大時間。
?*
?*
?* 分析:題目中的螞蟻只可能相遇在整數點,不可以相遇在其它點,比如3.5cm處之類的,也就是可以讓每只螞蟻走 1秒,然后
?* 查看是否有相遇的即可.
?*
?* 這樣我的程序實現思路就是,初始化5只螞蟻,讓每只螞蟻走1秒,然后看是否有相遇的,如果有則做相應處理.當每只螞蟻都
?* 走出木桿時,我就記錄當前時間.這樣就可以得到當前狀態情況下,需要多久可以走出木桿,然后遍歷所有狀態則可以得到所胡
?* 可能.
?*/
package baidu;
public class Ant {
?/*
? * step 表示螞蟻每一個單位時間所走的長度
? */
?private final static int step = 1;
?/*
? * position表示螞蟻所處的初始位置
? */
?private int position;
?/*
? * direction表示螞蟻的前進方向,如果為1表示向27厘米的方向走, 如果為-1,則表示往0的方向走。
? */
?private int direction = 1;
?/*
? * 此函數運行一次,表示螞蟻前進一個單位時間,如果已經走下木桿則會拋出異常
? */
?public void walk() {
??if (isOut()) {
???throw new RuntimeException("the ant is out");
??}
??position = position + this.direction * step;
?};
?/**
? * 檢查螞蟻是否已經走出木桿,如果走出返回true
? *
? */
?public boolean isOut() {
??return position <= 0 || position >= 27;
?}
?/**
? * 檢查此螞蟻是否已經遇到另外一只螞蟻
? * @param ant
? * @return 如果遇到返回true
? */
?public boolean isEncounter(Ant ant) {
??return ant.position == this.position;
?}
?/**
? * 改變螞蟻的前進方向
? */
?public void changeDistation() {
??direction = -1 * direction;
?}
?/**
? * 構造函數,設置螞蟻的初始前進方向,和初始位置
? * @param position
? * @param direction
? */
?public Ant(int position, int direction) {
??this.position = position;
??if (direction != 1) {
???this.direction = -1;//方向設置初始位置,比如為0時,也將其設置為1.這樣可以方便后面的處理
??} else {
???this.direction = 1;
??}
?}
}
?
/////////////////////////////////////////////////////////
package baidu;
public class Controller {
?public static void main(String[] args) {
??int time = 0;
??for (int i = 0; i < 32; i++) {
???Ant[] antArray = getAntList(getPoistions(), getDirections(i));
???while (!isAllOut(antArray)) {
????for (Ant ant : antArray) {
?????if (!ant.isOut()) {
??????ant.walk();
?????}
????}
????time++;
????// 查看是否有已經相遇的Ant,如果有則更改其前進方向
????dealEncounter(antArray);
???}
???System.out.println(time);
???// 將時間歸0,這樣可以重新設置條件,再次得到全部走完所需要的時間.
???time = 0;
??}
?}
?/**
? * 這個函數的算法很亂,但暫時能解決問題
? *
? * @param list
? */
?public static void dealEncounter(Ant[] antArray) {
??int num_ant = antArray.length;
??for (int j = 0; j < num_ant; j++) {
???for (int k = j + 1; k < num_ant; k++) {
????if (antArray[j].isEncounter(antArray[k])) {
?????antArray[j].changeDistation();
?????antArray[k].changeDistation();
????}
???}
??}
?}
?/**
? * 因為有5只Ant,所以組合之后有32種組合.剛好用5位二進制來表示,如果為0則表示Ant往0的方向走 如果為1,則表示往27的方向走
? *
? * 注:在通過Ant的構造函數設置初始值時,通過過濾把0修改成了-1.
? */
?public static int[] getDirections(int seed) {
??int result[] = new int[5];
??result[0] = seed % 2;
??result[1] = seed / 2 % 2;
??result[2] = seed / 4 % 2;
??result[3] = seed / 8 % 2;
??result[4] = seed / 16 % 2;
??System.out.println("directions is " + result[0] + "|" + result[1] + "|"
????+ result[2] + "|" + result[3] + "|" + result[4]);
??return result;
?}
?/**
? * 批量設置Ant的初始位置,這樣設置不是十分必要,可以直接在代碼中設置
? *
? * @return
? */
?public static int[] getPoistions() {
??return new int[] { 3, 7, 11, 17, 23 };
?}
?/**
? * 取得設置好初始值的5只Ant
? *
? * @param positions
? * @param directions
? * @return
? */
?public static Ant[] getAntList(int[] positions, int[] directions) {
??Ant ant3 = new Ant(positions[0], directions[0]);
??Ant ant7 = new Ant(positions[1], directions[1]);
??Ant ant11 = new Ant(positions[2], directions[2]);
??Ant ant17 = new Ant(positions[3], directions[3]);
??Ant ant23 = new Ant(positions[4], directions[4]);
??return new Ant[] { ant3, ant7, ant11, ant17, ant23 };
?}
?/**
? * 判斷是否所有的Ant都已經走出了木桿,也就是設置退出條件
? *
? * @param antArray
? * @return
? */
?public static boolean isAllOut(Ant[] antArray) {
??for (Ant ant : antArray) {
???if (ant.isOut() == false) {
????return false;
???}
??}
??return true;
?}
}
?
]]>
]]>