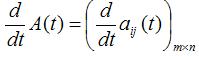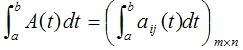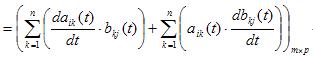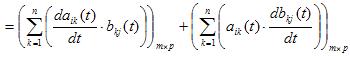1) 涓夎鍒嗚В娉?Triangular decomposition)
涓夎鍒嗚В娉曟槸灝嗘柟闃?FONT face="Times New Roman"> (square matrix)鍒嗚В鎴愪竴涓笂涓夎鐭╅樀錒濇垨鏄帓鍒?FONT face="Times New Roman">(permuted) 鐨勪笂涓夎鐭╅樀錒炲拰涓涓笅涓夎鐭╅樀錛岃鏂規硶鍙堣縐頒負LU鍒嗚В娉曘?BR> 渚嬪, 鐭╅樀X=[1 2 3;4 5 6;7 8 9], 榪愮敤璇ュ垎瑙ｆ柟娉曞彲浠ュ緱鍒?
涓婁笁瑙掔煩闃礚=[0.1429 1.0000 0
0.5714 0.5000 1.0000
1.0000 0 0]
鍜屼笅涓夎鐭╅樀U=[7.0000 8.0000 9.0000
0 0.8571 1.7143
0 0 0.0000]
涓嶉毦楠岃瘉 L* U = X.
璇ュ垎瑙ｆ柟娉曠殑鐢ㄩ斾富瑕佸湪綆鍖栧ぇ鐭╅樀鐨勮鍒楀紡鍊肩殑璁＄畻,鐭╅樀姹傞嗚繍綆楀拰姹傝В鑱旂珛鏂圭▼緇勩傞渶瑕佹敞鎰忕殑鏄? 榪欑鍒嗚В鏂規硶鎵寰楀埌鐨勪笂涓嬩笁瑙掑艦鐭╅樀涓嶆槸鍞竴鐨勶紝鎴戜滑榪樺彲鎵懼埌鑻ュ共瀵逛笉鍚岀殑涓婁笅涓夎鐭╅樀瀵癸紝瀹冧滑鐨勪箻縐篃浼氬緱鍒板師鐭╅樀銆?nbsp;
瀵瑰簲MATLAB鍛戒護: lu
2) QR鍒嗚В娉?/STRONG>
QR鍒嗚В娉曟槸灝嗙煩闃靛垎瑙ｆ垚涓涓崟浣嶆浜ょ煩闃?鑷韓涓庡叾杞疆涔樼Н涓哄崟浣嶉樀I)鍜屼竴涓笂涓夎鐭╅樀銆?nbsp;
瀵瑰簲MATLAB鍛戒護: qr
3) 濂囧紓鍊煎垎瑙ｆ硶(SVD)
濂囧紓鍊煎垎瑙?FONT face="Times New Roman"> (sigular value decomposition,SVD) 鏄彟涓縐嶆浜ょ煩闃靛垎瑙ｆ硶錛?FONT face="Times New Roman">SVD鏄渶鍙潬鐨勫垎瑙ｆ硶錛屼絾鏄畠姣?FONT face="Times New Roman">QR 鍒嗚В娉曡鑺變笂榪戝崄鍊嶇殑璁＄畻鏃墮棿銆備嬌鐢?FONT face="Times New Roman">SVD鍒嗚В娉曠殑鐢ㄩ旀槸姹傝В鏈灝忓鉤鏂硅宸拰鏁版嵁鍘嬬緝銆?
瀵瑰簲MATLAB鍛戒護: svd
]]>
This artical introduces the simplest theory of differential of matrix. Here, a matrix every element of which is a function of a variable is disscussed.(Quite simple, huh)
1. Definition
Let A be a matrix each element of which is a function of variable t,
If t is defined at a range from a and b, i.e., t鈭?/SPAN>[a, b], A(t) is claimed to be defined within region [a, b];
If each element aij(t) is continuous, differentiable, integrable, A(t) is said to be continuous, differentiable, integrable respectively.
When A(t) is differentiable, its differential is defined as
Similarly, the integral of A(t) when it鈥檚 integrable is defined as
2. Application
1). 
Proof:
2).
Proof:
Suppose 
, 
, the element at the ith row and jth
column of their product matrix A(t)B(t) is
Therefore,
|
Note The differential As a matter of fact, it is incorrect indeed. There is a quick and simple way to acquire yourself. A(t) is an m脳n dimensional matrix, and B(t) n脳p, so |
3). 
Proof:
The matrix tA=(taij)m脳n and the exponent function of tA is
According to the definition of the differential of matrix,
4). 
Proof:
The matrix tA=(taij)m脳n and the sine function of tA is
According to the definition of the differential of matrix,
Applying the same approach, we can proof its counterpart,
]]>