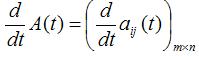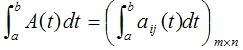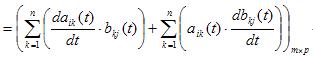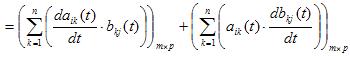Differential of matrix
Differential of matrix(1)
This artical introduces the simplest theory of differential of matrix. Here, a matrix every element of which is a function of a variable is disscussed.(Quite simple, huh)
1. Definition
Let A be a matrix each element of which is a function of variable t,
If t is defined at a range from a and b, i.e., t∈[a, b], A(t) is claimed to be defined within region [a, b];
If each element aij(t) is continuous, differentiable, integrable, A(t) is said to be continuous, differentiable, integrable respectively.
When A(t) is differentiable, its differential is defined as
Similarly, the integral of A(t) when it’s integrable is defined as
2. Application
1).
Proof:
2).
Proof:
Suppose ,
, the element at the ith row and jth
column of their product matrix A(t)B(t) is
Therefore,
|
Note The differential As a matter of fact, it is incorrect indeed. There is a quick and simple way to acquire yourself. A(t) is an m×n dimensional matrix, and B(t) n×p, so |
3).
Proof:
The matrix tA=(taij)m×n and the exponent function of tA is
According to the definition of the differential of matrix,
4).
Proof:
The matrix tA=(taij)m×n and the sine function of tA is
According to the definition of the differential of matrix,
Applying the same approach, we can proof its counterpart,
posted on 2005-12-29 17:37 Guo Zhang 閱讀(425) 評論(0) 編輯 收藏 所屬分類: 數(shù)理統(tǒng)計