1 歸并排序（MergeSort）
歸并排序最差運行時間是O(nlogn)，它是利用遞歸設計程序的典型例子。
歸并排序的最基礎的操作就是合并兩個已經排好序的序列。
假設我們有一個沒有排好序的序列，那么首先我們使用分割的辦法將這個序列分割成一個一個已經排好序的子序列。然后再利用歸并的方法將一個個的子序列合并成排序好的序列。分割和歸并的過程可以看下面的圖例。
從上圖可以看出，我們首先把一個未排序的序列從中間分割成2部分，再把2部分分成4部分，依次分割下去，直到分割成一個一個的數據，再把這些數據兩兩歸并到一起，使之有序，不停的歸并，最后成為一個排好序的序列。
如何把兩個已經排序好的子序列歸并成一個排好序的序列呢？可以參看下面的方法。
假設我們有兩個已經排序好的子序列。
序列A：1 23 34 65
序列B：2 13 14 87
那么可以按照下面的步驟將它們歸并到一個序列中。
（1）首先設定一個新的數列C[8]。
（2）A[0]和B[0]比較，A[0] = 1，B[0] = 2，A[0] < B[0]，那么C[0] = 1
（3）A[1]和B[0]比較，A[1] = 23，B[0] = 2，A[1] > B[0]，那么C[1] = 2
（4）A[1]和B[1]比較，A[1] = 23，B[1] = 13，A[1] > B[1]，那么C[2] = 13
（5）A[1]和B[2]比較，A[1] = 23，B[2] = 14，A[1] > B[2]，那么C[3] = 14
（6）A[1]和B[3]比較，A[1] = 23，B[3] = 87，A[1] < B[3]，那么C[4] = 23
（7）A[2]和B[3]比較，A[2] = 34，B[3] = 87，A[2] < B[3]，那么C[5] = 34
（8）A[3]和B[3]比較，A[3] = 65，B[3] = 87，A[3] < B[3]，那么C[6] = 65
（9）最后將B[3]復制到C中，那么C[7] = 87。歸并完成。
如果我們清楚了上面的分割和歸并過程，那么我們就可以用遞歸的方法得到歸并算法的實現。
public class MergeSorter
{
private static int[] myArray;
private static int arraySize;
public static void Sort( int[] a )
{
myArray = a;
arraySize = myArray.Length;
MergeSort();
}
/// <summary>
/// 利用歸并的方法排序數組，首先將序列分割
/// 然后將數列歸并，這個算法需要雙倍的存儲空間
/// 時間是O(nlgn)
/// </summary>
private static void MergeSort()
{
int[] temp = new int[arraySize];
MSort( temp, 0, arraySize - 1);
}
private static void MSort(int[] temp, int left, int right)
{
int mid;
if (right > left)
{
mid = (right + left) / 2;
MSort( temp, left, mid); //分割左邊的序列
MSort(temp, mid+1, right);//分割右邊的序列
Merge(temp, left, mid+1, right);//歸并序列
}
}
private static void Merge( int[] temp, int left, int mid, int right)
{
int i, left_end, num_elements, tmp_pos;
left_end = mid - 1;
tmp_pos = left;
num_elements = right - left + 1;
while ((left <= left_end) && (mid <= right))
{
if (myArray[left] <= myArray[mid]) //將左端序列歸并到temp數組中
{
temp[tmp_pos] = myArray[left];
tmp_pos = tmp_pos + 1;
left = left +1;
}
else//將右端序列歸并到temp數組中
{
temp[tmp_pos] = myArray[mid];
tmp_pos = tmp_pos + 1;
mid = mid + 1;
}
}
while (left <= left_end) //拷貝左邊剩余的數據到temp數組中
{
temp[tmp_pos] = myArray[left];
left = left + 1;
tmp_pos = tmp_pos + 1;
}
while (mid <= right) //拷貝右邊剩余的數據到temp數組中
{
temp[tmp_pos] = myArray[mid];
mid = mid + 1;
tmp_pos = tmp_pos + 1;
}
for (i=0; i < num_elements; i++) //將所有元素拷貝到原始數組中
{
myArray[right] = temp[right];
right = right - 1;
}
}
}
歸并排序算法是一種O(nlogn)的算法。它的最差，平均，最好時間都是O(nlogn)。但是它需要額外的存儲空間，這在某些內存緊張的機器上會受到限制。
歸并算法是又分割和歸并兩部分組成的。對于分割部分，如果我們使用二分查找的話，時間是O(logn)，在最后歸并的時候，時間是O(n)，所以總的時間是O(nlogn)。
2 堆排序（HeapSort）
堆排序屬于百萬俱樂部的成員。它特別適合超大數據量（百萬條記錄以上）的排序。因為它并不使用遞歸（因為超大數據量的遞歸可能會導致堆棧溢出），而且它的時間也是O(nlogn)。還有它并不需要大量的額外存儲空間。
堆排序的思路是:
(1)將原始未排序的數據建成一個堆。
(2)建成堆以后，最大值在堆頂，也就是第0個元素，這時候將第零個元素和最后一個元素交換。
(3)這時候將從0到倒數第二個元素的所有數據當成一個新的序列，建一個新的堆，再次交換第一個和最后一個元素，依次類推，就可以將所有元素排序完畢。
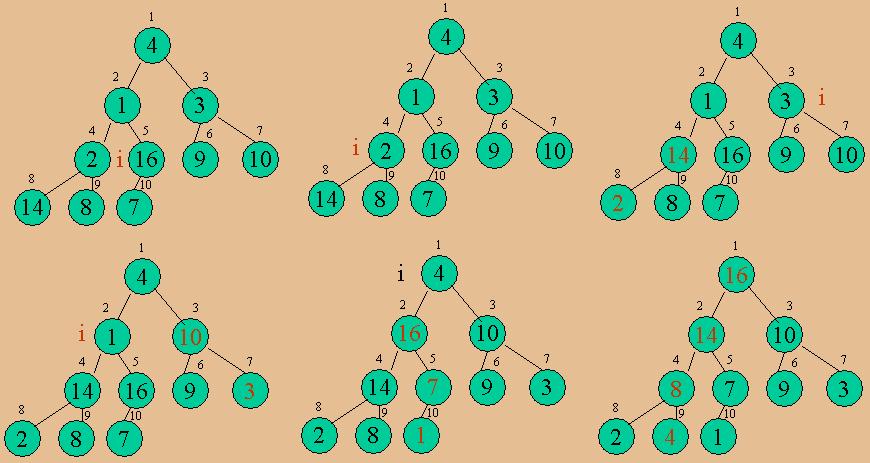
建立堆的過程如下面的圖所示:
堆排序的具體算法如下：
public class HeapSorter
{
private static int[] myArray;
private static int arraySize;
public static void Sort( int[] a )
{
myArray = a;
arraySize = myArray.Length;
HeapSort();
}
private static void HeapSort()
{
BuildHeap(); //將原始序列建成一個堆
while ( arraySize > 1 )
{
arraySize--;
Exchange ( 0, arraySize );//將最大值放在數組的最后
DownHeap ( 0 ); //將序列從0到n-1看成一個新的序列，重新建立堆
}
}
private static void BuildHeap()
{
for (int v=arraySize/2-1; v>=0; v--)
DownHeap ( v );
}
//利用向下遍歷子節點建立堆
private static void DownHeap( int v )
{
int w = 2 * v + 1; // 節點w是節點v的第一個子節點
while (w < arraySize)
{
if ( w+1 < arraySize ) // 如果節點v下面有第二個字節點
if ( myArray[w+1] > myArray[w] )
w++; // 將子節點w設置成節點v下面值最大的子節點
// 節點v已經大于子節點w，有了堆的性質，那么返回
if ( myArray[v] >= myArray[w] )
return;
Exchange( v, w ); // 如果不是，就交換節點v和節點w的值
v = w;
w = 2 * v + 1; // 繼續向下找子節點
}
}
//交換數據
private static void Exchange( int i, int j )
{
int t = myArray[i];
myArray[i] = myArray[j];
myArray[j] = t;
}
}
堆排序主要用于超大規模的數據的排序。因為它不需要額外的存儲空間，也不需要大量的遞歸。3 幾種O(nlogn)算法的初步比較我們可以從下表看到幾種O(nlogn)算法的效率的區別。所有的數據都使用.Net的Random類產生，每種算法運行100次，時間的單位為毫秒。
| 500隨機整數 | 5000隨機整數 | 20000隨機整數 |
| 合并排序 | 0.3125 | 1.5625 | 7.03125 |
| Shell排序 | 0.3125 | 1.25 | 6.875 |
| 堆排序 | 0.46875 | 2.1875 | 6.71875 |
| 快速排序 | 0.15625 | 0.625 | 2.8125 |
從上表可以明顯地看出，快速排序是最快的算法。這也就給了我們一個結論，對于一般的應用來說，我們總是選擇快速排序作為我們的排序算法，當數據量非常大（百萬數量級）我們可以使用堆排序，如果內存空間非常緊張，我們可以使用Shell排序。但是這意味著我們不得不損失速度。 /****************************************************************************************** *【Author】：flyingbread *【Date】：2007年2月2日 *【Notice】： *1、本文為原創技術文章，首發博客園個人站點(http://flyingbread.cnblogs.com/)，轉載和引用請注明作者及出處。 *2、本文必須全文轉載和引用，任何組織和個人未授權不能修改任何內容，并且未授權不可用于商業。 *3、本聲明為文章一部分，轉載和引用必須包括在原文中。 ******************************************************************************************/