Posted on 2011-04-21 23:36
沙漠中的魚 閱讀(425)
評論(0) 編輯 收藏 所屬分類:
Java 、
Java基礎
Java 語言支持兩種基本的浮點類型： float 和 double ，以及與它們對應的包裝類 Float 和 Double 。它們都依據 IEEE 754 標準，該標準為 32 位浮點和 64 位雙精度浮點二進制小數定義了二進制標準。
IEEE 754 用科學記數法以底數為 2 的小數來表示浮點數。IEEE 浮點數用 1 位表示數字的符號，用 8 位來表示指數，用 23 位來表示尾數，即小數部分。作為有符號整數的指數可以有正負之分。小數部分用二進制（底數 2）小數來表示，這意味著最高位對應著值 ?(2 -1)，第二位對應著 ?(2 -2)，依此類推。對于雙精度浮點數，用 11 位表示指數，52 位表示尾數。IEEE 浮點值的格式如圖 1 所示。
圖 1. IEEE 754 浮點數的格式
因為用科學記數法可以有多種方式來表示給定數字，所以要規范化浮點數，以便用底數為 2 并且小數點左邊為 1 的小數來表示，按照需要調節指數就可以得到所需的數字。所以，例如，數 1.25 可以表示為尾數為 1.01，指數為 0： (-1) 0*1.01 2*2 0
數 10.0 可以表示為尾數為 1.01，指數為 3： (-1) 0*1.01 2*2 3
一個十進制數能否用二進制浮點數精確表示，關鍵在于小數部分。我們來看一個最簡單的小數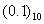
能否精確表示。按照乘以2取整數位的方法，有：
得到一個無限循環的二進制小數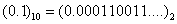
，用有限位無法表示無限循環小數，因此，
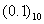無法用IEEE 754浮點數精確表示。從中也可以看到：由于
，
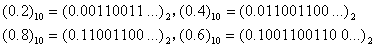這四個數也無法精確表示。同理：
也無法用IEEE 754浮點數精確表示。
在以0.1~0.9結尾的9個小數中，只有0.5可以精確表示：（如）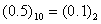
，而其他均無法進行精確轉換。