回旋矩陣算法題解題思路(無須存儲矩陣)
深圳一家公司面試問題,很囧http://www.javaeye.com/topic/545378?page=1
題目要求打印一個回旋數字矩陣
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
int i=6
1 2 3 4 5 6
20 21 22 23 24 7
19 32 33 34 25 8
18 31 36 35 26 9
17 30 29 28 27 10
16 15 14 13 12 11
我的解題思路分析:
1.將此矩陣分解為一個一個的圈,如下圖,1-20可以看成一個圈,21-32是一個圈,33-36也是一個圈。

2.再將圈分解為四個均等的數列
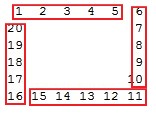
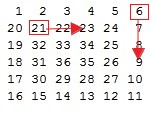
3.打印的過程中用一個二維數組存儲矩陣,記錄圈數 ,當前圈的數列長度 和圈開始計數的數字 。如i=6,第1圈時數列長為5,開始計數的數字為0;第2圈數列長為3,開始計數的數字為20;從這些規律總結出,已知變長為i,假設當前圈數為count,則數列長step=i-1-count*2

/**
* @author Heis
* @date Dec 11, 2009
*/
public class SnakeNum {
public static void main(String[] args){
int i=6;
SnakeNum.print(SnakeNum.fill(i));
}
/**
*
* 算法復雜度為n
* 以下的算法,在for循環內的一些計算是不必要的,可以用變量保存,但是為了代碼更加直觀,就不做優化了。
*
* @param i 矩陣邊長
*/
public static int[][] fill(int i){
Long startTime=System.currentTimeMillis();
//第幾圈
int count=0;
//數列長度
int step;
//總圈數
int all;
//某圈開始計數的基數
int startNum=0;
//用于數組下標計算
int startIndex;
int k;
int[][] array=null;
if(i>0){
array=new int[i][i];
all=i/2+i%2;
while(all>=count){
step=i-1-(count<<1);
count++;
for(startIndex=count-1,k=1;k<step+1;k++){
array[count-1][startIndex++]=startNum+k;
}
for(startIndex=count-1,k=1;k<step+1;k++){
array[startIndex++][i-count]=startNum+k+step;
}
for(startIndex=i-count,k=1;k<step+1;k++){
array[i-count][startIndex--]=startNum+k+2*step;
}
for(startIndex=i-count,k=1;k<step+1;k++){
array[startIndex--][count-1]=startNum+k+3*step;
}
startNum=4*step+startNum;
}
//當矩陣邊長為基數時,打印最后一個數字
if(i%2>0){
int mid=all-1;
array[mid][mid]=i*i;
}
}
Long timeUsed=System.currentTimeMillis()-startTime;
System.out.println("總用時:"+timeUsed+"ms");
return array;
}
/**
* 打印數組
*
* @param array
*/
public static void print(int[][] array){
if(array!=null){
int n=array.length;
int i=0,j;
int count=Integer.valueOf(n*n).toString().length()+1;
for(;i<n;i++){
for(j=0;j<n;j++){
System.out.printf("%"+count+"d",array[i][j]);
}
System.out.println();
}
}
}
}
優化后的代碼:
/**
* @author Heis
*
*/
public class SnakeNum2 {
public static void main(String[] args){
int i=6;
SnakeNum2.print(SnakeNum2.fill(i));
}
/**
*
* 算法復雜度為n
* @param i 矩陣邊長
*/
public static int[][] fill(int i){
Long startTime=System.currentTimeMillis();
//第幾圈
int count=0;
//轉彎步數
int step;
//總圈數
int all;
//某圈開始累加的基數
int startNum=0;
//用于數組下標計算
int startIndex;
int k,cache=0;
int[][] array=null;
if(i>0){
array=new int[i][i];
all=i/2+i%2;
while(all>=count){
step=i-1-(count<<1);
count++;
for(startIndex=count-1,k=1;k<step+1;k++){
array[count-1][startIndex++]=startNum+k;
}
for(startIndex=count-1,k=1;k<step+1;k++){
array[startIndex++][i-count]=startNum+k+step;
}
cache=(step<<1)+startNum;
for(startIndex=i-count,k=1;k<step+1;k++){
array[i-count][startIndex--]=cache+k;
}
cache=(step<<1)+startNum+step;
for(startIndex=i-count,k=1;k<step+1;k++){
array[startIndex--][count-1]=cache+k;
}
startNum=(step<<2)+startNum;
}
//當矩陣邊長為基數時,打印最后一個數字
if(i%2>0){
int mid=all-1;
array[mid][mid]=i*i;
}
}
Long timeUsed=System.currentTimeMillis()-startTime;
System.out.println("總用時:"+timeUsed+"ms");
return array;
}
/**
* 打印數組
*
* @param array
*/
public static void print(int[][] array){
if(array!=null){
int n=array.length;
int i=0,j;
int count=Integer.valueOf(n*n).toString().length()+1;
for(;i<n;i++){
for(j=0;j<n;j++){
System.out.printf("%"+count+"d",array[i][j]);
}
System.out.println();
}
}
}
}
回帖還有另外一種思路,也是用一個二維數組存儲數組,按照數列順序輸出,在輸出過程中判斷輸出的方向,可以看這里的代碼http://www.javaeye.com/topic/545378?page=1#1288013
package circle_out;
public class TestCricleOut {
public static void main(String[] args){
output(6);
}
public static void output(int N){
for(int i=1;i<=N;i++){
for(int j=1;j<=N;j++){
int count=getValue(i, j, N);
System.out.print(count+"\t");
}
System.out.println();
}
}
public static int smallest(int i,int j,int k,int m){
int tmp=0;
if(i<=j){
tmp=i;
}else{
tmp=j;
}
if(tmp>k){
tmp=k;
}
if(tmp>m){
tmp=m;
}
return tmp;
}
public static int getValue(int i,int j,int N){
int index=0;
int small=smallest(i, j, N-i+1, N-j+1);
index=getCountByCircle(small, N);
if(i==small){
index+=j-small+1;
}else if(N-j+1==small){
index+=N-2*(small-1)+(i-small);
}else if(N-i+1==small){
index+=2*(N-2*(small-1))-1+(N-j-small+1);
}else{
index+=3*(N-2*(small-1))-3+(N-small-i+1)+1;
}
return index;
}
public static int getCountByCircle(int circle,int count){
int total=0;
for(int i=1;i<circle;i++){
total+=getCircle(count-2*(i-1));
}
return total;
}
public static int getCircle(int count){
return 4*count-4;
}
}


