Suppose n1, n2, …, nk are positive integers which are pairwise coprime. Then, for any given integers a1,a2, …, ak, there exists an integer x solving the system of simultaneous congruences
Furthermore, all solutions x to this system are congruent modulo the product N = n1n2…nk.
Hence 
for all 
, if and only if 
.
Sometimes, the simultaneous congruences can be solved even if the ni's are not pairwise coprime. A solution x exists if and only if:
All solutions x are then congruent modulo the least common multiple of the ni.
Versions of the Chinese remainder theorem were also known to Brahmagupta (7th century), and appear in Liber Abaci (1202).
[edit] A constructive algorithm to find the solution
This algorithm only treats the situations where the ni's are coprime. The method of successive substitution can often yield solutions to simultaneous congruences, even when the moduli are not pairwise coprime.
Suppose, as above, that a solution is needed to the system of congruences:
Again, to begin, the product 
is defined. Then a solution x can be found as follows.
For each i the integers ni and N / ni are coprime. Using the extended Euclidean algorithm we can therefore find integers ri and si such that rini + siN / ni = 1. Then, choosing the label ei = siN / ni, the above expression becomes:
Consider ei. The above equation guarantees that its remainder, when divided by ni, must be 1. On the other hand, since it is formed as siN / ni, the presence of N guarantees that it's evenly divisible by any nj so long as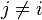 
.
Because of this, combined with the multiplication rules allowed in congruences, one solution to the system of simultaneous congruences is:
For example, consider the problem of finding an integer x such that
Using the extended Euclidean algorithm for 3 and 4×5 = 20, we find (−13) × 3 + 2 × 20 = 1, i.e. e1 = 40. Using the Euclidean algorithm for 4 and 3×5 = 15, we get (−11) × 4 + 3 × 15 = 1. Hence, e2 = 45. Finally, using the Euclidean algorithm for 5 and 3×4 = 12, we get 5 × 5 + (−2) × 12 = 1, meaning e3 = −24. A solution x is therefore 2 × 40 + 3 × 45 + 1 × (−24) = 191. All other solutions are congruent to 191 modulo 60, (3 × 4 × 5 = 60) which means that they are all congruent to 11 modulo 60.
NOTE: There are multiple implementations of the extended Euclidean algorithm which will yield different sets of e1, e2, and e3. These sets however will produce the same solution i.e. 11 modulo 60.
extended Enclidean algorithm
[edit] Informal formulation of the algorithm
| Dividend | Divisor | Quotient | Remainder |
|---|---|---|---|
| 120 | 23 | 5 | 5 |
| 23 | 5 | 4 | 3 |
| 5 | 3 | 1 | 2 |
| 3 | 2 | 1 | 1 |
| 2 | 1 | 2 | 0 |
It is assumed that the reader is already familiar with .
To illustrate the extension of the Euclid's algorithm, consider the computation of gcd(120, 23), which is shown on the table on the left. Notice that the quotient in each division is recorded as well alongside the remainder.
In this case, the remainder in the fourth line (which is equal to 1) indicates that the gcd is 1; that is, 120 and 23 are coprime (also called relatively prime). For the sake of simplicity, the example chosen is a coprime pair; but the more general case of gcd other than 1 also works similarly.
There are two methods to proceed, both using the division algorithm, which will be discussed separately.
[edit] The iterative method
This method computes expressions of the form ri = axi + byi for the remainder in each step i of the Euclidean algorithm. Each modulus can be written in terms of the previous two remainders and their whole quotient as follows:
By substitution, this gives:
The first two values are the initial arguments to the algorithm:
- r1 = a = a(1) + b(0)
- r2 = b = a(0) + b(1)
The expression for the last non-zero remainder gives the desired results since this method computes every remainder in terms of a and b, as desired.
Example: Compute the GCD of 120 and 23.
The computation proceeds as follows:
| Step | Quotient | Remainder | Substitute | Combine terms | |
|---|---|---|---|---|---|
| 1 | 120 | 120 = 120 * 1 + 23 * 0 | |||
| 2 | 23 | 23 = 120 * 0 + 23 * 1 | |||
| 3 | 5 | 5 = 120 - 23 * 5 | 5 = (120 * 1 + 23 * 0) - (120 * 0 + 23 * 1) * 5 | 5 = 120 * 1 + 23 * -5 | |
| 4 | 4 | 3 = 23 - 5 * 4 | 3 = (120 * 0 + 23 * 1) - (120 * 1 + 23 * -5) * 4 | 3 = 120 * -4 + 23 * 21 | |
| 5 | 1 | 2 = 5 - 3 * 1 | 2 = (120 * 1 + 23 * -5) - (120 * -4 + 23 * 21) * 1 | 2 = 120 * 5 + 23 * -26 | |
| 6 | 1 | 1 = 3 - 2 * 1 | 1 = (120 * -4 + 23 * 21) - (120 * 5 + 23 * -26) * 1 | 1 = 120 * -9 + 23 * 47 | |
| 7 | 2 | 0 | End of algorithm | ||
The last line reads 1 = −9×120 + 47×23, which is the required solution: x = −9 and y = 47.
This also means that −9 is the multiplicative inverse of 120 modulo 23, and that 47 is the multiplicative inverse of 23 modulo 120.
- −9 × 120 ≡ 1 mod 23 and also 47 × 23 ≡ 1 mod 120.
[edit] The recursive method
This method attempts to solve the original equation directly, by reducing the dividend and divisor gradually, from the first line to the last line, which can then be substituted with trivial value and work backward to obtain the solution.
Consider the original equation:
| 120 | x | + | 23 | y | = | 1 |
| (5×23+5) | x | + | 23 | y | = | 1 |
| 23 | (5x+y) | + | 5 | x | = | 1 |
| ... | ||||||
| 1 | a | + | 0 | b | = | 1 |
Notice that the equation remains unchanged after decomposing the original dividend in terms of the divisor plus a remainder, and then regrouping terms. If we have a solution to the equation in the second line, then we can work backward to find x and y as required. Although we don't have the solution yet to the second line, notice how the magnitude of the terms decreased (120 and 23 to 23 and 5). Hence, if we keep applying this, eventually we'll reach the last line, which obviously has (1,0) as a trivial solution. Then we can work backward and gradually find out x and y.
| Dividend | = | Quotient | x | Divisor | + | Remainder |
|---|---|---|---|---|---|---|
| 120 | = | 5 | x | 23 | + | 5 |
| 23 | = | 4 | x | 5 | + | 3 |
| ... | ||||||
For the purpose of explaining this method, the full working will not be shown. Instead some of the repeating steps will be described to demonstrate the principle behind this method.
Start by rewriting each line from the first table with division algorithm, focusing on the dividend this time (because we'll be substituting the dividend).
| 120 | x0 | + | 23 | y0 | = | 1 |
| (5×23+5) | x0 | + | 23 | y0 | = | 1 |
| 23 | (5x0+y0) | + | 5 | x0 | = | 1 |
| 23 | x1 | + | 5 | y1 | = | 1 |
| (4×5+3) | x1 | + | 5 | y1 | = | 1 |
| 5 | (4x1+y1) | + | 3 | x1 | = | 1 |
| 5 | x2 | + | 3 | y2 | = | 1 |
|
[edit] The table method
The table method is probably the simplest method to carry out with a pencil and paper. It is similar to the recursive method, although it does not directly require algebra to use and only requires working in one direction. The main idea is to think of the equation chain as a sequence of divisors . In the running example we have the sequence 120, 23, 5, 3, 2, 1. Any element in this chain can be written as a linear combination of the original x and y, most notably, the last element, gcd(x,y), can be written in this way. The table method involves keeping a table of each divisor, written as a linear combination. The algorithm starts with the table as follows:
| a | b | d |
| 1 | 0 | 120 |
| 0 | 1 | 23 |
The elements in the d column of the table will be the divisors in the sequence. Each di can be represented as the linear combination . The a and b values are obvious for the first two rows of the table, which represent x and y themselves. To compute di for any i > 2, notice that . Suppose . Then it must be that and . This is easy to verify algebraically with a simple substitution.
Actually carrying out the table method though is simpler than the above equations would indicate. To find the third row of the table in the example, just notice that 120 divided by 23 goes 5 times plus a remainder. This gives us k, the multiplying factor for this row. Now, each value in the table is the value two rows above it, minus k times the value immediately above it. This correctly leads to , , and . After repeating this method to find each line of the table (note that the remainder written in the table and the multiplying factor are two different numbers!), the final values for a and b will solve :
| a | b | d |
| 1 | 0 | 120 |
| 0 | 1 | 23 |
| 1 | -5 | 5 |
| -4 | 21 | 3 |
| 5 | -26 | 2 |
| -9 | 47 | 1 |
This method is simple, requiring only the repeated application of one rule, and leaves the answer in the final row of the table with no backtracking. Note also that if you end up with a negative number as the answer for the factor of, in this case b, you will then need to add the modulus in order to make it work as a modular inverse (instead of just taking the absolute value of b). I.e. if it returns a negative number, don't just flip the sign, but add in the other number to make it work. Otherwise it will give you the modular inverse yielding negative one.
]]>
参考解{?/h3>
动态规划算法可有效地解此问题。下面我们按照动态规划算法设计的各个步骤来设计一个解此问题的有效法?/p>
1.最长公共子序列的结?/h4>
解最长公共子序列问题时最Ҏ惛_的算法是ID搜烦法，卛_X的每一个子序列Q检查它是否也是Y的子序列Q从而确定它是否为X和Y的公共子序列Qƈ 且在查过E中选出最长的公共子序列。X的所有子序列都检查过后即可求出X和Y的最长公共子序列。X的一个子序列相应于下标序列{1, 2, …, m}的一个子序列Q因此，X共有2m个不同子序列Q从而穷举搜索法需要指数时间?/p>
事实上，最长公共子序列问题也有最优子l构性质Q因为我们有如下定理Q?/p>
定理: LCS的最优子l构性质
讑ֺ列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的一个最长公共子序列Z=<z1, z2, …, zk>Q则Q?/p>
- 若xm=ynQ则zk=xm=yn且Zk-1是Xm-1和Yn-1的最长公共子序列Q?
- 若xm≠yn且zk≠xm Q?/sub>则Z是Xm-1和Y的最长公共子序列Q?
- 若xm≠yn且zk≠yn Q则Z是X和Yn-1的最长公共子序列?
其中Xm-1=<x1, x2, …, xm-1>QYn-1=<y1, y2, …, yn-1>QZk-1=<z1, z2, …, zk-1>?/p>
证明
- 用反证法。若zk≠xmQ则<z1, z2, …, zk ,xm >是X和Y的长度ؓk?的公共子序列。这与Z是X和Y的一个最长公共子序列矛盾。因此，必有zk=xm=yn。由此可知Zk-1是Xm-1和Yn-1的一个长度ؓk-1的公共子序列。若Xm-1和Yn-1有一个长度大于k-1的公共子序列WQ则xm加在其尾部将产生X和Y的一个长度大于k的公共子序列。此为矛盾。故Zk-1是Xm-1和Yn-1的一个最长公共子序列?
- ׃zk≠xmQZ是Xm-1和Y的一个公共子序列。若Xm-1和Y有一个长度大于k的公共子序列WQ则W也是X和Y的一个长度大于k的公共子序列。这与Z是X和Y的一个最长公共子序列矛盾。由此即知Z是Xm-1和Y的一个最长公共子序列?
- ?2.cM?
q个定理告诉我们Q两个序列的最长公共子序列包含了这两个序列的前~的最长公共子序列。因此，最长公共子序列问题h最优子l构性质?/p>
2.子问题的递归l构
由最长公共子序列问题的最优子l构性质可知Q要扑ևX=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的最长公共子序列Q可按以下方式递归地进行：当xm=ynӞ扑ևXm-1和Yn-1的最长公共子序列Q然后在其尾部加上xm(=yn)卛_得X和Y的一个最长公共子序列。当xm≠ynӞ必须解两个子问题Q即扑ևXm-1和Y的一个最长公共子序列及X和Yn-1的一个最长公共子序列。这两个公共子序列中较长者即为X和Y的一个最长公共子序列?/p>
由此递归l构Ҏ看到最长公共子序列问题h子问题重叠性质。例如，在计X和Y的最长公共子序列Ӟ可能要计出X和Yn-1及Xm-1和Y的最长公共子序列。而这两个子问题都包含一个公共子问题Q即计算Xm-1和Yn-1的最长公共子序列?/p>
与矩阵连乘积最优计次序问题类|我们来徏立子问题的最优值的递归关系。用c[i,j]记录序列Xi和Yj的最长公共子序列的长度。其中Xi=<x1, x2, …, xi>QYj=<y1, y2, …, yj>。当i=0或j=0ӞI序列是Xi和Yj的最长公共子序列Q故c[i,j]=0。其他情况下Q由定理可徏立递归关系如下Q?/p>
3.计算最优?/h4>
直接利用(2.2)式容易写Z个计c[i,j]的递归法Q但其计时间是随输入长度指数增长的。由于在所考虑的子问题I间中，d只有θ(m*n)个不同的子问题，因此Q用动态规划算法自底向上地计算最优D提高法的效率?/p>
计算最长公共子序列长度的动态规划算法LCS_LENGTH(X,Y)以序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>作ؓ输入。输Z个数lc[0..m ,0..n]和b[1..m ,1..n]。其中c[i,j]存储Xi与Yj的最长公共子序列的长度，b[i,j]记录指示c[i,j]的值是由哪一个子问题的解辑ֈ的，q在构造最长公共子序列时要用到。最后，X和Y的最长公共子序列的长度记录于c[m,n]中?/p>
Procedure LCS_LENGTH(X,Y);
begin
m:=length[X];
n:=length[Y];
for i:=1 to m do c[i,j]:=0;
for j:=1 to n do c[0,j]:=0;
for i:=1 to m do
for j:=1 to n do
if x[i]=y[j] then
begin
c[i,j]:=c[i-1,j-1]+1;
b[i,j]:="?;
end
else if c[i-1,j]≥c[i,j-1] then
begin
c[i,j]:=c[i-1,j];
b[i,j]:="↑";
end
else
begin
c[i,j]:=c[i,j-1];
b[i,j]:="←"
end;
return(c,b);
end;
׃每个数组单元的计耗费Ο(1)旉Q算法LCS_LENGTH耗时Ο(mn)?/p>
4.构造最长公共子序列
q法LCS_LENGTH计算得到的数lb可用于快速构造序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的最长公共子序列。首先从b[m,n]开始，沿着其中的箭头所指的方向在数lb中搜索。当b[i,j]中遇??Ӟ表示Xi与Yj的最长公共子序列是由Xi-1与Yj-1的最长公共子序列在尾部加上xi得到的子序列Q当b[i,j]中遇?↑"Ӟ表示Xi与Yj的最长公共子序列和Xi-1与Yj的最长公共子序列相同Q当b[i,j]中遇?←"Ӟ表示Xi与Yj的最长公共子序列和Xi与Yj-1的最长公共子序列相同?/p>
下面的算法LCS(b,X,i,j)实现Ҏb的内Ҏ印出Xi与Yj的最长公共子序列。通过法的调用LCS(b,X,length[X],length[Y])Q便可打印出序列X和Y的最长公共子序列?/p>
Procedure LCS(b,X,i,j);
begin
if i=0 or j=0 then return;
if b[i,j]="? then
begin
LCS(b,X,i-1,j-1);
print(x[i]); {打印x[i]}
end
else if b[i,j]="↑" then LCS(b,X,i-1,j)
else LCS(b,X,i,j-1);
end;
在算法LCS中，每一ơ的递归调用使i或j?Q因此算法的计算旉?em>O(m+n)?/p>
例如Q设所l的两个序列为X=<AQBQCQBQDQAQB>和Y=<BQDQCQAQBQA>。由法LCS_LENGTH和LCS计算出的l果如图2所C?/p>
| j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | |||||||||
| i | yj | B | D | C | A | B | A | |||||||||
| ?/td> | ─ | ─ | ─ | ─ | ─ | ─ | ─ | ─ | ─ | ─ | ─ | ─ | ─ | ?/td> | ||
| 0 | xi | ?/td> | 0 | 0 | 0 | 0 | 0 | 0 | ?/td> | |||||||
| ?/td> | ↑ | ↑ | ↑ | ?/td> | ?/td> | ?/td> | ||||||||||
| 1 | A | ?/td> | 0 | 0 | 0 | 0 | 1 | ← | 1 | 1 | ?/td> | |||||
| ?/td> | ?/td> | ↑ | ?/td> | ?/td> | ||||||||||||
| 2 | B | ?/td> | 0 | 1 | ← | 1 | ← | 1 | 1 | 2 | ← | 2 | ?/td> | |||
| ?/td> | ↑ | ↑ | ?/td> | ↑ | ↑ | ?/td> | ||||||||||
| 3 | C | ?/td> | 0 | 1 | 1 | 2 | ← | 2 | 2 | 2 | ?/td> | |||||
| ?/td> | ?/td> | ↑ | ↑ | ↑ | ?/td> | ?/td> | ||||||||||
| 4 | B | ?/td> | 0 | 1 | 1 | 2 | 2 | 3 | ← | 3 | ?/td> | |||||
| ?/td> | ↑ | ?/td> | ↑ | ↑ | ↑ | ↑ | ?/td> | |||||||||
| 5 | D | ?/td> | 0 | 1 | 2 | 2 | 2 | 3 | 3 | ?/td> | ||||||
| ?/td> | ↑ | ↑ | ↑ | ?/td> | ↑ | ?/td> | ?/td> | |||||||||
| 6 | A | ?/td> | 0 | 1 | 2 | 2 | 3 | 3 | 4 | ?/td> | ||||||
| ?/td> | ?/td> | ↑ | ↑ | ↑ | ?/td> | ↑ | ?/td> | |||||||||
| 7 | B | ?/td> | 0 | 1 | 2 | 2 | 3 | 4 | 5 | ?/td> | ||||||
| ?/td> | ─ | ─ | ─ | ─ | ─ | ─ | ─ | ─ | ─ | ─ | ─ | ─ | ─ | ?/td> |
? 法LCS的计结?/font>
5.法的改q?/h4>
对于一个具体问题，按照一般的法设计{略设计出的法Q往往在算法的旉和空间需求上q可以改q。这U改q，通常是利用具体问题的一些特D性?/p>
例如Q在法LCS_LENGTH和LCS中，可进一步将数组b省去。事实上Q数l元素c[i,j]的g由c[i-1,j-1]Qc[i-1, j]和c[i,j-1]三个g一定Q而数l元素b[i,j]也只是用来指Cc[i,j]I竟由哪个值确定。因此，在算法LCS中，我们可以不借助于数 lb而借助于数lc本n临时判断c[i,j]的值是由c[i-1,j-1]Qc[i-1,j]和c[i,j-1]中哪一个数值元素所定Q代hΟ(1)旉。既然b对于法LCS不是必要的，那么法LCS_LENGTH便不必保存它。这一来，可节?em>θ(mn)的空_而LCS_LENGTH和LCS所需要的旉分别仍然?em>Ο(mn)?em>Ο(m+n)。不q，׃数组c仍需?em>Ο(mn)的空_因此q里所作的改进Q只是在I间复杂性的常数因子上的改进?/p>
另外Q如果只需要计最长公共子序列的长度，则算法的I间需求还可大大减。事实上Q在计算c[i,j]Ӟ只用到数lc的第i行和Wi-1行。因此，只要?行的数组I间可以计出最长公共子序列的长度。更q一步的分析q可空间需求减至min(m, n)?/p>