摩尔定律�l�制下的软�g开发时代有一个非常有意思的现象�Q�”Andy giveth, and Bill taketh away.”。不���CPU的主频有多快�Q�我们始�l�有办法来利用它�Q�而我们也陉���在机器升�U�带来的�E�序性能提高中�?/p>
我记着我大二的时候曾�l�做�q�一个五子棋的程序,当时的算法就是预先设计一些棋型(有优先���Q�,然后扫描���盘�Q�对形势�q�行分析�Q�看看当前走哪部对自己最重要。当然下���还要堵别�h�Q�这���需要互换双方的���型再计���。如果只���一步,很可能被狡猾的对手欺骗,所以�ؓ(f��)�?ji��n)多惛_��步,�q�需要递归和回朔。在当时的机器上�Q�算3步就基本上需�?�U�左右的旉����?ji��n)。后来大学毕业收拾东西的时候找到这个程序,试了(ji��n)一下,发现��?0步需要的旉���也基本上感觉不出来了(ji��n)�?/p>
不知道你是否有同��L(f��ng)���l�历�Q�我们不知不觉的一直在享受着�q�样的免费午���。可是,随着摩尔定律的提前终�l�,免费的午���终�I�要�q�回厅R��虽然硬件设计师�q�在努力�Q�Hyper Threading CPU�Q�多��Z��套寄存器�Q�相当于一个逻辑CPU�Q���得Pipeline���可能满负荷�Q���多个Thread的操作有可能�q�行�Q���得多�U�程�E�序的性能�?%-15%的提升;增加Cache定w��也��得包括Single-Thread和Multi-Thread�E�序都能受益。也许这些还能帮助你一�D�|����_(d��)��但问题是�Q�我们必���d��出改变,面对�q�个卛_��到来的变革,你准备好�?ji��n)么�Q?/p>
Concurrency Programming != Multi-Thread Programming。很多�h都会(x��)说MultiThreading谁不�?x��),问题是,你是��Z��么���?如何使用多线�E�的�Q�我从前做过一个类似AcdSee一��L(f��ng)��囑փ�查看/处理�E�序�Q�我通常用它来处理我的数码照片。我在里面用�?ji��n)大量的多线�E�,不过主要目的是在囑փ�处理的时候不要Block住UI�Q�所以将CPU Intensive的计���部分用后台�U�程�q�行处理。而�ƈ没有把对囑փ�矩阵的运����ƈ行分开�?/p>
我觉得Concurrency Programming真正的挑战在于Programming Model的改变,在程序员的脑子里面要对自��q���E�序怎样�q�行化有很清楚的认识�Q�更重要的是�Q�如何去实现�Q�包括架构、容错、实时监控等�{�)(j��)�q�种�q�行化,如何�?strong>调试�Q�如何去���试�?/p>
在Google�Q�每天有���量的数据需要在有限的时间内�q�行处理�Q�其实每个互联网公司都会(x��)���到�q�样的问题)(j��)�Q�每个程序员都需要进行分布式的程序开发,�q�其中包括如何分布、调度、监控以�?qi��ng)容错等�{�。Google�?a >MapReduce正是把分布式的业务逻辑从这些复杂的�l�节中抽象出来,使得没有或者很����ƈ行开发经验的�E�序员也能进行�ƈ行应用程序的开发�?/p>
MapReduce中最重要的两个词���是Map�Q�映���)(j��)和Reduce�Q�规�U�)(j��)。初看Map/Reduce�q�两个词�Q�熟�(zh��n)�Function Language的�h一定感觉很熟�?zh��n)�。FP把这��L(f��ng)��函数�U�Cؓ(f��)”higher order function”(”High order function”被成�ؓ(f��)Function Programming的利器之一哦)(j��)�Q�也���是��_(d��)���q�些函数是编写来被与其它函数相结合(或者说被其它函数调用的�Q�。如果说���要比的化,可以把它惌���成C里面的CallBack函数�Q�或者STL里面的Functor。比如你要对一个STL的容器进行查找,需要制定每两个元素相比较的Functor�Q�Comparator�Q�,�q�个Comparator在遍历容器的时候就�?x��)被调用�?/p>
拿前面说�q�图像处理程序来举例�Q�其实大多数的图像处理操作都是对囑փ�矩阵�q�行某种�q�算。这里的�q�算通常有两�U�,一�U�是映射�Q�一�U�是规约。拿两种效果来说�Q�”老照片”效果通常是强化照片的G/B��|��然后�Ҏ(gu��)��个象素加一些随机的偏移�Q�这些操作在二维矩阵上的每一个元素都是独立的�Q�是Map操作。而”雕删Z��效果需要提取图像边�~�,���需要元素之间的�q�算�?ji��n),是一�U�Reduce操作。再举个���单的例子�Q�一个一�l�矩阵(数组�Q�[0,1,2,3,4]可以映射为[0,2,3,6,8]�Q�乘2�Q�,也可以映����ؓ(f��)[1,2,3,4,5]�Q�加1�Q�。它可以规约�?�Q�元素求�U�)(j��)也可以规�U��ؓ(f��)10�Q�元素求和)(j��)�?/p>
面对复杂问题�Q�古人教导我们要�?strong>�?/strong>�?strong>�?/strong>之”,英文中对应的词是�?strong>Divide and Conquer“。Map/Reduce其实���是Divide/Conquer的过�E�,通过把问题Divide�Q��ɘq�些Divide后的Map�q�算高度�q�行�Q�再���Map后的�l�果Reduce�Q�根据某一个Key�Q�,得到最�l�的�l�果�?/p>
Googler发现�q�是问题的核�?j��),其它都是共性问题。因此,他们把MapReduce抽象分离出来。这��P��Google的程序员可以只关�?j��)应用逻辑�Q�关�?j��)根据哪些Key把问题进行分解,哪些操作是Map操作�Q�哪些操作是Reduce操作。其它�ƈ行计���中的复杂问题诸如分布、工作调度、容错、机器间通信都交�l�Map/Reduce Framework��d���Q�很大程度上���化了(ji��n)整个�~�程模型�?/p>
MapReduce的另一个特�Ҏ(gu��)���Q�Map和Reduce�?strong>输入和输出都是中间��(f��)时文�?/strong>�Q�MapReduce利用Google文�g�pȝ��来管理和讉K���q�些文�g�Q�,而不是不同进�E�间或者不同机器间的其它通信方式。我觉得�Q�这是Google一贯的风格�Q�化�J��ؓ(f��)����Q�返璞归真�?/p>
接下来就放下其它�Q�研�I�一下Map/Reduce操作。(其它比如定w��、备份�Q务也有很�l�典的经验和实现�Q�论文里面都有详�q�ͼ�(j��)
Map的定义:(x��)
Map, written by the user, takes an input pair and produces a set of intermediate key/value pairs. The MapReduce library groups together all intermediate values associated with the same intermediate key I and passes them to the Reduce function.
Reduce的定义:(x��)
The Reduce function, also written by the user, accepts an intermediate key I and a set of values for that key. It merges together these values to form a possibly smaller set of values. Typically just zero or one output value is produced per Reduce invocation. The intermediate values are supplied to the user’s reduce function via an iterator. This allows us to handle lists of values that are too large to fit in memory.
MapReduce论文中给��Z��(ji��n)�q�样一个例子:(x��)在一个文档集合中�l�计每个单词出现的次数�?/p>
Map操作的输入是每一���文档,���输入文档中每一个单词的出现输出��C��间文件中厅R�?/p>
map(String key, String value):
// key: document name
// value: document contents
for each word w in value:
EmitIntermediate(w, �?�?;
比如我们有两���文档,内容分别�?/p>
A �Q?“I love programming�?/p>
B �Q?“I am a blogger, you are also a blogger”�?/p>
B文档�l�过Map�q�算后输出的中间文�g���会(x��)是:(x��)
I,1 am,1 a,1 blogger,1 you,1 are,1 a,1 blogger,1
Reduce操作的输入是单词和出现次数的序列。用上面的例子来��_(d��)�����是 (”I�? [1, 1]), (”love�? [1]), (”programming�? [1]), (”am�? [1]), (”a�? [1,1]) �{�。然后根据每个单词,���出�ȝ��出现�ơ数�?/p>
reduce(String key, Iterator values):
// key: a word
// values: a list of counts
int result = 0;
for each v in values:
result += ParseInt(v);
Emit(AsString(result));
最后输出的最�l�结果就�?x��)是�Q?”I�? 2�?, (”a�? 2�?…�?/p>
实际的执行顺序是�Q?/p>
- MapReduce Library���Input分成M份。这里的Input Splitter也可以是多台机器�q�行Split�?
- Master���M份Job分给Idle状态的M个worker来处理;
- 对于输入中的每一�?lt;key, value> pair �q�行Map操作�Q�将中间�l�果Buffer在Memory里;
- 定期的(或者根据内存状态)(j��)�Q�将Buffer中的中间信息Dump�?strong>本地���盘上,�q�且把文件信息传回给Master�Q�Master需要把�q�些信息发送给Reduce worker�Q�。这里最重要的一�Ҏ(gu��)���Q?strong>在写���盘的时候,需要将中间文�g做Partition�Q�比如R个)(j��)。拿上面的例子来举例�Q�如果把所有的信息存到一个文�Ӟ��Reduce worker又会(x��)变成瓉���。我们只需要保�?strong>相同Key能出现在同一个Partition里面���可以把�q�个问题分解�?
- R个Reduce worker开始工作,从不同的Map worker的Partition那里拿到数据�Q?strong>read the buffered data from the local disks of the map workers�Q�,用key�q�行排序�Q�如果内存中放不下需要用到外部排�?- external sort�Q�。很昄����Q�排序(或者说Group�Q�是Reduce函数之前必须做的一步�?�q�里面很关键的是�Q�每个Reduce worker�?x��)去从很多Map worker那里拿到X(0<X<R) Partition的中间结果,�q�样�Q�所有属于这个Key的信息已�l�都在这个worker上了(ji��n)�?
- Reduce worker遍历中间数据�Q�对每一个唯一Key�Q�执行Reduce函数�Q�参数是�q�个key以及(qi��ng)相对应的一�p�d��Value�Q��?
- 执行完毕后,唤醒用户�E�序�Q�返回结果(最后应该有R份Output�Q�每个Reduce Worker一个)(j��)�?
可见�Q�这里的分(Divide�Q�体现在两步�Q�分别是���输入分成M份,以及(qi��ng)���Map的中间结果分成R份。将输入分开通常很简单,Map的中间结果通常用”hash(key) mod R”这个结果作为标准,保证相同的Key出现在同一个Partition里面。当�?d��ng)���使用者也可以指定自己的Partition Function�Q�比如,对于Url Key�Q�如果希望同一个Host的URL出现在同一个Partition�Q�可以用”hash(Hostname(urlkey)) mod R”作为Partition Function�?/p>
对于上面的例子来��_(d��)��每个文档中都可能�?x��)出现成千上万�?(”the�? 1)�q�样的中间结果,琐碎的中间文件必然导致传输上的损失。因此,MapReduce�q�支持用��h��供Combiner Function。这个函数通常与Reduce Function有相同的实现�Q�不同点在于Reduce函数的输出是最�l�结果,而Combiner函数的输出是Reduce函数的某一个输入的中间文�g�?/p>
Tom White�l�出�?ji��n)Nutch[2]中另一个很直观的例子,分布式Grep。我一直觉得,Pipe中的很多操作�Q�比如More、Grep、Cat都类��g��一�U�Map操作�Q�而Sort、Uniq、wc�{�都相当于某�U�Reduce操作�?/p>
加上前两天Google刚刚发布�?a >BigTable论文�Q�现在Google有了(ji��n)自己的集��?- Googel Cluster�Q�分布式文�g�pȝ�� - GFS�Q�分布式计算环境 - MapReduce�Q�分布式�l�构化存�?- BigTable�Q�再加上Lock Service。我真的能感觉的到Google著名的免�Ҏ(gu��)�����之外的对于�E�序员的另一�U�免费的晚餐�Q�那个由大量的commodity PC�l�成的large clusters。我觉得�q�些才真正是Google的核�?j��)�h(hu��n)值所在�?/p>
呵呵�Q�就像微软老兵Joel Spolsky�Q�你应该看过他的”Joel on Software”吧�Q�)(j��)曄���说过�Q�对于微软来说最可怕的是[1]�Q�微软还在苦苦追赶Google来完善Search功能的时候,Google已经在部�|�下一代的�����计算��Z��(ji��n)�?/p>
The very fact that Google invented MapReduce, and Microsoft didn’t, says something about why Microsoft is still playing catch up trying to get basic search features to work, while Google has moved on to the next problem: building Skynet^H^H^H^H^H^H the world’s largest massively parallel supercomputer. I don’t think Microsoft completely understands just how far behind they are on that wave.
�?�Q�其实,微��Y也有自己的方�?- DryAd。问题是�Q�大公司里,要想重新部��v�q�样一个底层的InfraStructure�Q�无论是技术的原因�Q�还是政�ȝ��原因�Q�将是如何的难�?/p>
�?�Q?a >Lucene之父Doug Cutting的又一力作�Q�Project Hadoop - 由Hadoop分布式文件系�l�和一个Map/Reduce的实现组成,Lucene/Nutch的成产线也够齐全的了(ji��n)�?br />
from: http://xerdoc.com/blog/archives/246.html
One day, you're browsing through your code, and you notice two big blocks that look almost exactly the same. In fact, they're exactly the same, except that one block refers to "Spaghetti" and one block refers to "Chocolate Moose."
// A trivial example:
alert("I'd like some Spaghetti!");
alert("I'd like some Chocolate Moose!");
These examples happen to be in JavaScript, but even if you don't know JavaScript, you should be able to follow along.
The repeated code looks wrong, of course, so you create a function:
function SwedishChef( food )
{
alert("I'd like some " + food + "!");
}
SwedishChef("Spaghetti");
SwedishChef("Chocolate Moose");
OK, it's a trivial example, but you can imagine a more substantial example. This is better code for many reasons, all of which you've heard a million times. Maintainability, Readability, Abstraction = Good!
Now you notice two other blocks of code which look almost the same, except that one of them keeps calling this function called BoomBoom and the other one keeps calling this function called PutInPot. Other than that, the code is pretty much the same.

alert("get the lobster");
PutInPot("lobster");
PutInPot("water");
alert("get the chicken");
BoomBoom("chicken");
BoomBoom("coconut");
Now you need a way to pass an argument to the function which itself is a function. This is an important capability, because it increases the chances that you'll be able to find common code that can be stashed away in a function.
function Cook( i1, i2, f )
{
alert("get the " + i1);
f(i1);
f(i2);
}
Cook( "lobster", "water", PutInPot );
Cook( "chicken", "coconut", BoomBoom );
Look! We're passing in a function as an argument.
Can your language do this?
Wait... suppose you haven't already defined the functions PutInPot or BoomBoom. Wouldn't it be nice if you could just write them inline instead of declaring them elsewhere?
Cook( "lobster",
"water",
function(x) { alert("pot " + x); } );
Cook( "chicken",
"coconut",
function(x) { alert("boom " + x); } );
Jeez, that is handy. Notice that I'm creating a function there on the fly, not even bothering to name it, just picking it up by its ears and tossing it into a function.
As soon as you start thinking in terms of anonymous functions as arguments, you might notice code all over the place that, say, does something to every element of an array.
var a = [1,2,3];
for (i=0; i<a.length; i++)
{
a[i] = a[i] * 2;
}
for (i=0; i<a.length; i++)
{
alert(a[i]);
}
Doing something to every element of an array is pretty common, and you can write a function that does it for you:
function map(fn, a)
{
for (i = 0; i < a.length; i++)
{
a[i] = fn(a[i]);
}
}
Now you can rewrite the code above as:
map( function(x){return x*2;}, a );
map( alert, a );
Another common thing with arrays is to combine all the values of the array in some way.
function sum(a)
{
var s = 0;
for (i = 0; i < a.length; i++)
s += a[i];
return s;
}
function join(a)
{
var s = "";
for (i = 0; i < a.length; i++)
s += a[i];
return s;
}
alert(sum([1,2,3]));
alert(join(["a","b","c"]));
sum and join look so similar, you might want to abstract out their essence into a generic function that combines elements of an array into a single value:
function reduce(fn, a, init)
{
var s = init;
for (i = 0; i < a.length; i++)
s = fn( s, a[i] );
return s;
}
function sum(a)
{
return reduce( function(a, b){ return a + b; },
a, 0 );
}
function join(a)
{
return reduce( function(a, b){ return a + b; },
a, "" );
}
Many older languages simply had no way to do this kind of stuff. Other languages let you do it, but it's hard (for example, C has function pointers, but you have to declare and define the function somewhere else). Object-oriented programming languages aren't completely convinced that you should be allowed to do anything with functions.
Java required you to create a whole object with a single method called a functor if you wanted to treat a function like a first class object. Combine that with the fact that many OO languages want you to create a whole file for each class, and it gets really klunky fast. If your programming language requires you to use functors, you're not getting all the benefits of a modern programming environment. See if you can get some of your money back.
How much benefit do you really get out of writting itty bitty functions that do nothing more than iterate through an array doing something to each element?
Well, let's go back to that map function. When you need to do something to every element in an array in turn, the truth is, it probably doesn't matter what order you do them in. You can run through the array forward or backwards and get the same result, right? In fact, if you have two CPUs handy, maybe you could write some code to have each CPU do half of the elements, and suddenly map is twice as fast.
Or maybe, just hypothetically, you have hundreds of thousands of servers in several data centers around the world, and you have a really big array, containing, let's say, again, just hypothetically, the entire contents of the internet. Now you can run map on thousands of computers, each of which will attack a tiny part of the problem.
So now, for example, writing some really fast code to search the entire contents of the internet is as simple as calling the map function with a basic string searcher as an argument.
The really interesting thing I want you to notice, here, is that as soon as you think of map and reduce as functions that everybody can use, and they use them, you only have to get one supergenius to write the hard code to run map and reduce on a global massively parallel array of computers, and all the old code that used to work fine when you just ran a loop still works only it's a zillion times faster which means it can be used to tackle huge problems in an instant.
Lemme repeat that. By abstracting away the very concept of looping, you can implement looping any way you want, including implementing it in a way that scales nicely with extra hardware.
And now you understand something I wrote a while ago where I complained about CS students who are never taught anything but Java:
Without understanding functional programming, you can't invent MapReduce, the algorithm that makes Google so massively scalable. The terms Map and Reduce come from Lisp and functional programming. MapReduce is, in retrospect, obvious to anyone who remembers from their 6.001-equivalent programming class that purely functional programs have no side effects and are thus trivially parallelizable. The very fact that Google invented MapReduce, and Microsoft didn't, says something about why Microsoft is still playing catch up trying to get basic search features to work, while Google has moved on to the next problem: building Skynet^H^H^H^H^H^H the world's largest massively parallel supercomputer. I don't think Microsoft completely understands just how far behind they are on that wave.
Ok. I hope you're convinced, by now, that programming languages with first-class functions let you find more opportunities for abstraction, which means your code is smaller, tighter, more reusable, and more scalable. Lots of Google applications use MapReduce and they all benefit whenever someone optimizes it or fixes bugs.
And now I'm going to get a little bit mushy, and argue that the most productive programming environments are the ones that let you work at different levels of abstraction. Crappy old FORTRAN really didn't even let you write functions. C had function pointers, but they were ugleeeeee and not anonymous and had to be implemented somewhere else than where you were using them. Java made you use functors, which is even uglier. As Steve Yegge points out, Java is the Kingdom of Nouns.
Correction: The last time I used FORTRAN was 27 years ago. Apparently it got functions. I must have been thinking about GW-BASIC.
About the Author: I'm your host, Joel Spolsky, a software developer in New York City. Since 2000, I've been writing about software development, management, business, and the Internet on this site. For my day job, I run Fog Creek Software, makers of FogBugz - the smart bug tracking software with the stupid name, and Fog Creek Copilot - the easiest way to provide remote tech support over the Internet, with nothing to install or configure.
from: http://www.joelonsoftware.com/items/2006/08/01.html
- General Idea
- Examples (in Scheme or in C)
- Interest
Program Specialization
Let us consider a program P, taking two arguments S and D, and producing a result R:
A specialization of P with respect to S is a program PS such that, for all input D,
Input S is called static, it is known (i.e., available) at specialization time. Input D is dynamic, it is unknown (i.e., unavailable) until run time.
Specialization Examples
Program specialization makes sense in any programming language. Consider for example the following Scheme program. (See below for more examples, in C.)
-
(define (append list1 list2) (if (null? list1) list2 (cons (car list1) (append (cdr list1) list2))))
A possible specialization of append with respect to a static argument list1 = (4 2) is function append42 below.
-
(define (append42 list2) (cons 4 (cons 2 list2)))
Function append42 preserves the semantics of append, or more precisely, it has the same semantics as the trivial specialization function triv_append42, defined as
-
(define (triv-append42 list2) (append '(4 2) list2))
Depending on the context, S is called a specialization value or an invariant. In the general case, a specialization may exploit several invariants, whether input values or constants already present in the code of P.
Interest of Specialization
The interest of function append42 above, as opposed to triv-append42, is that computations depending only on the static input list1 = (4 2) have already been performed. More generally, specialization impacts on speed and size of programs, thus offering applications to program optimization.
- Speed
- Specialization factors out computations from the specialized program. As a result, a specialized program runs faster than the original program. (Although, in some rare cases, cache effects may yield a slight slowdown.) For example, function
append42above runs faster thanappend(or more precisely,triv-append42) because the traversal of argumentlist1as already been performed. - Size
- A specialized program is sometimes smaller than the original program (e.g., when a static input corresponds to an option that dispatches on different functionalities of the program). It is sometimes bigger (e.g., when a loop or a recursive call is unfolded).
Note that all program arguments do not have the same impact on specialization. For example, specializing append with respect to list2 = (4 2) leads to the quite unexciting function below.
-
(define (dull-append42 list1) (if (null? list1) '(4 2) (cons (car list1) (dull-append42 (cdr list1)))))
Specialization is used in particular (sometimes unknowingly) to optimize critical sections of code. It is often handwritten.
Partial Evaluation
Partial evaluation (PE) is the process that automates program specialization [CD93, DRT96, JGS93]. A partial evaluator (or specializer) is a program M that takes two arguments, the source of a program P and a static (known) subset of the input S, and produces a specialized program PS:
Roughly speaking, partial evaluation can be thought of as a combination of aggressive constant folding, inlining, loop unrolling and inter-procedural constant propagation applied to all data types (including pointers, structures and arrays) instead of just scalars.
Applications of Partial Evaluation
Handwritten specialization is tedious, error-prone and does not scale to large programs. Because it is automatic, specialization via partial evaluation does not have all those drawbacks; it is even predictable (see below). As a result, specialization becomes an issue in engineering software: it is possible to rapidly write generic programs, which are maintainable but slow, and automatically produce fast specialized instances. Because the programmer focuses less on optimization hacks, and more on reusability, partial evaluation greatly improve productivity and program safety.
Partial evaluation has been successfully applied as an optimizer in various domains such as operating systems and networking, computer graphics, numerical computation, circuit simulation, software architectures, compiling and compiler generation.
It has also been used for program understanding and reengineering: given various running options, partial evaluation may split large programs into smaller ones.
Off-line vs. On-line Partial Evaluation
An on-line partial evaluator takes as arguments the source of a program P and a static subset of the input S, performs symbolic computations on available data, and directly yields the source of a specialized program PS.
In an off-line partial evaluator, the specialization is divided into two steps. First, an program binding-time analysis propagate abstract information about static and dynamic values throughout the code. It prepares the second phase that, given actual specialization values, produce specialized code.
On-line partial evaluator are theoretically more powerful: specialization relies on actual values, not on the fact that values are known. On the other hand, off-line partial evaluator are faster because value propagation is "pre-compiled". Moreover, they are predictable in the sense that it is possible to assess the degree of specialization.
Some partial evaluators, like Tempo, can specialize programs not only at compile time (i.e., source-to-source transformation) but also run time (i.e., run-time code generation). Only off-line partial evaluation lends itself to run-time specialization.
Binding-Time Analysis
As a first step, the user provides a program and specifies initial binding times, that is, which arguments (including global variables) are static (i.e., known) and which are dynamic (i.e., yet unknown). For example, the user provides the following code for aminiprintf function, and specifies that the first argument is static whereas the second is dynamic: miniprintf(S,D).
miniprintf(char fmt[], int val[]) { int i = 0; while( *fmt != '\0' ) { if( *fmt != '%' ) putchar(*fmt); else switch(*++fmt) { case 'd' : putint(val[i++]); break; case '%' : putchar('%'); break; default : prterror(*fmt); break; } fmt++; } }
Binding-time analysis (BTA) propagates the static/dynamic information throughout the program and annotates each statement and expression with a binding time. These annotations can be visualized using colors (or font effects).
/* LEGEND: STATICDYNAMIC */ miniprintf(char fmt[],int val[]){int i = 0;while( *fmt != '\0' ) {if( *fmt != '%' )putchar(*fmt);elseswitch(*++fmt) {case 'd' :putint(val[i++]);break;case '%' :putchar('%');break;default :prterror(*fmt);break;}fmt++;}}
The blue color (bold face for black and white display) represent static constructions, i.e. values that can be computed at specialization time. The red color (standard font for black and white display) is for dynamic expressions, whose value cannot be precomputed knowing only the static arguments. Basically, everything in blue (bold) will disappear after specialization; only red (standard font) parts will remain. Visualizing of the analysis is very important for the user to assess the amount of specialization in the code.
Note that in the case of languages like C, the binding-time analysis must takes into account pointer aliases and side-effects.
Compile-Time Specialization
When the user is satisfied with the analysis (i.e., what the user expects to specialize is indeed considered as static by the BTA), actual specialization values must be provided. For example, giving"<%d|%d>" as the actual specialization value for the fmt argument of the miniprintf() function yields the following specialized code.
miniprintf_1(int val[]) { putchar( '<' ); putint ( val[0] ); putchar( '|' ); putint ( val[1] ); putchar( '>' ); }
Run-Time Specialization
Partial evaluators like Tempo [CHL+98,CHN+96] can also perform run-time specialization [CN96], using optimized binary code templates [NHCL97]. A dedicated run-time specializer is generated from the results of the program analysis. In the case of theminiprintf function, a runtime specializer rts_miniprintf() is generated, which can be used as in the following example.
/* * Some dynamic execution context setting variable 'format' */ spec_printf = rts_miniprintf(format); // specialize ... (*spec_printf)(val1); // <=> miniprintf(format,val1) (*spec_printf)(val2); // <=> miniprintf(format,val2)
The function rts_miniprintf() is a dedicated runtime specializer. It returns a pointer to the specialized function. Several specialized versions can also be generated and used at the same time.
References
Various resources concerning partial evaluation, including existing specializers, PE-related events and basic references are accessible from pe_resources.php3.
- [CD93]
- Tutorial Notes on Partial Evaluation. C. Consel and O. Danvy. In ACM Symposium on Principles of Programming Languages, pages 493-501, 1993.
- [CHL+98]
- C. Consel, L. Hornof, J. Lawall, R. Marlet, G. Muller, J. Noyé, S. Thibault, and N. Volanschi. Tempo: Specializing systems applications and beyond. ACM Computing Surveys, Symposium on Partial Evaluation, 1998. To appear.
- [CHN+96]
- C. Consel, L. Hornof, F. Noël, J. Noyé, and E.N. Volanschi. A uniform approach for compile-time and run-time specialization. In O. Danvy, R. Glück, and P. Thiemann, editors, Partial Evaluation, International Seminar, Dagstuhl Castle, number 1110 in Lecture Notes in Computer Science, pages 54-72, February 1996.
- [CN96]
- C. Consel and F. Noël. A general approach for run-time specialization and its application to C. In Conference Record of the 23rd Annual ACM SIGPLAN-SIGACT Symposium on Principles Of Programming Languages, pages 145-156, St. Petersburg Beach, FL, USA, January 1996. ACM Press.
- [DRT96]
- Partial Evaluation. O. Danvy, R. Glück and P. Thiemann (Eds.). Lecture Notes in Computer Science, Vol. 1110.
- [JGS93]
- Partial evaluation and automatic program generation. N.D. Jones, C. Gomard and P. Sestoft. Prentice Hall international series in computer science, 1993.
- [NHCL97]
- F. Noël, L. Hornof, C. Consel, and J. Lawall. Automatic, template-based run-time specialization : Implementation and experimental study. In International Conference on Computer Languages, Chicago, IL, May 1998. IEEE Computer Society Press. Also available as IRISA report PI-1065.
Last modified: 2003-09-25. - Jocelyn.Frechot@labri.fr - http://compose.labri.fr
from: http://compose.labri.fr/documentation/pe/pe_overview.php3
密码学是理论计算机的一个很大的方向。之前准备先写密码学概论再提在hash函数破解上做出重大�A(ch��)献的王小云教授的工作�Q�不�q�前两天王小云获得求是杰出科学家奖以�?00万奖�?/a>�Q�在媒体上又掀起了(ji��n)一轮宣传狂潮,但是有些报道极端弱智�Q�错误百出,所以我���机�U�正一下,�q�介�l�密码学的一个组成部分——hash函数�Q�以�?qi��ng)王���云在这上面的工作�?/p>
王小云的主要工作是关于hash函数的破解工作。她�?005一个密码学�?x��)议上宣布破解�?ji��n)SHA-1�Q�震惊了(ji��n)全世界。所以要介绍和理解她的工作,先看一下hash函数具体是怎么回事�?/p>
���单的��_(d��)��hash函数���是把�Q意长的输入字�W�串变化成固定长的输出字�W�串的一�U�函数。通俗得说�Q�hash函数用来生成信息的摘要。输出字�W�串的长度称为hash函数�?strong>位数�?/p>
目前应用最为广泛的hash函数�?strong>SHA-1�?strong>MD5�Q�大多是128位和更长�?/p>
hash函数在现实生�z�M��应用十分�q�泛。很多下载网站都提供下蝲文�g的MD5码校验,可以用来判别文�g是否完整。另外,比如在WordPress的数据库�Q�所有密码都是保存的MD5码,�q�样即��数据库的���理员也无法知道用户的原始密码,避免隐私泄露�Q�很多�h在不同地斚w��是用的同一个密码)(j��)�?/p>
如果两个输入串的hash函数的��g����P��则称�q�两个串是一�?strong>���撞(Collision)。既然是把�Q意长度的字符串变成固定长度的字符�Ԍ��所以,必有一个输��Z��对应无穷多个输入�Ԍ�����撞是必然存在的�?/p>
一个“优良”的hash函数 f 应当满��以下三个条�g�Q?/p>
上面的“非常困�䏀�的意思是除了(ji��n)枚�D外不可能有别的更快的�Ҏ(gu��)��。比如第3条,�Ҏ(gu��)��生日定理�Q�要��x��到这��L(f��ng)��x1�Q�x2�Q�理��Z��需要大�U?^(n/2)的枚举次数�?/p>
几乎所有的hash函数的破解,都是指的破坏上面的第三条性质�Q�即扑ֈ�一个碰撞(前两条都能被破坏的hash函数也太�׃��(ji��n)点,早就被�h抛弃�?ji��n)�?j��)。在密码学上�q�有一个概忉|��理论破解�Q�指的是提出一个算法,使得可以用低于理论值得枚�D�ơ数扑ֈ����撞�?/p>
王小云的主要工作是给��Z��(ji��n)MD5�Q?a target="_blank">SHA-0
看到�q�里�Q�那些认��Z��国国安局应该���这些结果封存作为秘密武器甚臛_��想用�q�些成果来袭�ȝ��国之徒可以停住你们的YY�?ji��n)。这�U��Ş式上的破解,在大多数情况下没有实际性的作用。更别提MD5早就被美国�h抛弃�?ji��n)�?/p>
但是�Q�说�q�种破解一点实际意义都没有�Q�那��׃���׃��(ji��n)�q�大密码学家的智商,密码学家不会(x��)无缘无故的弄出碰撞这么一个概忉|��。下面简单的介绍一下在特定情况下,怎么利用�l�定的碰撞来做坏�?���译�?a target="_blank">Attacking Hash Functions)�Q?/p>
Caesar�l�实�?f��n)生Alice叫写�?ji��n)一���推荐信(letter)。同一天,Alice叫Caesar在推荐信上数字签名,�q�提供了(ji��n)一份推荐信的电(sh��)子板。Caesar打开文�g�Q�发现和原�g一模一栗���所以他在文件上�{�了(ji��n)名�?/p>
几个月后�Q�Caesar发现他的�U�密文�g被非法察看。这到底是怎么回事呢?


a25f7f0b 29ee0b39 68c86073 8533a4b9
事实上,Alice要求Caesar�{��的文�?a target="_blank">letter已经被Alice做了(ji��n)手脚�Q�准���地��_(d��)��Alice�q�准备了(ji��n)另外一个文�?a target="_blank">order�Q�它们的MD5码完全一致。而Caesar的数字签名还依赖于MD5���法�Q�所以Alice用order文�g替换Letter文�g之后�Q�Caesar的数字签名依然有效。那���order�l�Alice提供�?ji��n)察看秘密文件的权限�?/p>
具体的实现方法可�?a target="_blank">Hash Functions and the Blind Passenger Attack。我在这里简单的解释一�?只是大致思�\�Q�具体实现方式,需要对文�g�l�构信息有所�?ji��n)�?�Q?/p>
letter文�g的内�Ҏ(gu��)���Q?/p>
if(x1==x1) show "letter" else show "order"
order文�g的内�Ҏ(gu��)���Q?/p>
if(x2==x1) show "letter" else show "order"
其中字符�?letter"�?order"代表两封信实际显�C�的内容。x1�Q�x2是一个MD5的碰撞�?/p>
上面的方法,只供参考和学术用途,实际使用所引�v的后果概不负责�?/p>
参考:(x��)
- Attacking Hash Functions by Poisoned Messages "The Story of Alice and her Boss"
- Hash function, wikipedia
- SHA, wikipedia
- Interview with Yiqun Lisa Yin concerning the attack on SHA-1
PS�Q�我跟王���云老师的接触很���,上过俩次她的讨论班而已�Q�亦感觉到王���云老师的严谨和耐心(j��)。在��d��一个Turing奖获得者的演讲上,王小云提问的时候竟口而出“I ask who”的中式��p���Q�在引�v哄笑的同�Ӟ��我也极端佩服她的勇气。也许只有这��h��能做出非常好的工作吧�?/p>
PS2: wikipedia在国内可以通过free_door���览�?
http://zhiqiang.org/blog/446.html
参阅: 王小�?/a>,
概述�Q?br />
假设�?个schema�Q�S1和S2。我们要为S1里每一个元素在S2中找到匹配的元素�?br /> �q�程如下�Q?br /> 1. G1 = SQL2Graph(S1); G2 = SQL2Graph(S2); 把schema变成图,��N��用了(ji��n)Open Information Model (OIM)规格�Q�图中node采用矩�Ş和卵形,矩�Ş是文字描�q�ͼ�卵�Ş是标识符
2. initialMap = StringMatch(G1, G2); 用字�W�串匚w��做�ؓ(f��)初始匚w���Q�主要是比较通常的前�~�和后�~��Q�这��L(f��ng)���l�果通常是不准确�?br />
3. product = SFJoin(G1, G2, initialMap); 用SF���法生成�l�果�?font color="#0000ff">假设两个不同的节�Ҏ(gu��)���怼�的,则它们邻接元素的�怼�度增加。经�q�一�p�d��的�P代,�q�种�怼�度会(x��)传遍整个�?br />
4. result = SelectThreshold(product); �l�果�{��?br />
SF���法
图中的每条边�Q�用一个三元组表示�Q�s�Q�p�Q�o�Q�,分别�?源点�Q�边名,目的炏V�?br />
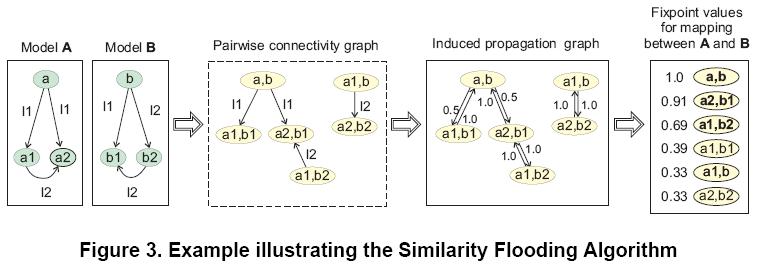
�怼�度传播图�Q�首先定义pairwise connectivity graph(PCG) �Q?((x; y); p; (x'; y')) 属于 PCG(A;B)<==>(x; p; x') �?A and (y; p; y') �?B�?关键是p要相同,也就是边的名字一栗��?/font>式子从右向左推导�Q�就可以A、B从两个模型徏立�v它们的PCG�?/font>图中的每个节点,都是A和B中的元素构成�?元组�Q�叫做map pairs�?br /> induced propagation graph。从PCG推导而来�Q�加上了(ji��n)反向的边�Q�边上注明了(ji��n)[传播�p�L��]�Q���gؓ(f��) 1/n�Q�n为相应的边的数目�?br /> 不动点计���:(x��)
设�?x; y) > 0 代表�?ji��n)节点x �?A �?y �?B 的相似度�Q�是在整个 A X B的范围上定义的。我们把 �Q(m��o) 叫做 mapping。相似度的计���就是基于�?values的�P代计���。设 �Q(m��o)i 代表�?ji��n)�?i �ơ�P代后的结果,�Q(m��o)0 是初始相似度�Q�可以用字符串相似度的办法的得出�Q�在我们的例子里�Q�没�?�Q(m��o)0 �Q�即�?�Q(m��o)0 =1�Q��?br /> 每次�q�代中,�Q(m��o)-values 都会(x��)�Ҏ(gu��)��光���居paris�?�Q(m��o)-values 乘以[传播�p�L��] 来增加。例如,在第一�ơ�P�?�Q(m��o)1(a1; b1) = �Q(m��o)0(a1; b1) + �Q(m��o)0(a; b) * 0.5 = 1.5。类似的�Q��?sup>1(a, b) = �Q(m��o)0(a, b) + �Q(m��o)0(a1; b1) * 1.0 + �Q(m��o)0(a2, b1) *1.0 = 3.0。接下来�Q�所�?�Q(m��o) ��D��行正规化�Q�比如除以当前�P代的 �Q(m��o)的最大��|��保证所�?�Q(m��o) 都不大于1。所以在正规化以后,�Q(m��o)1(a; b) = 1.0, �Q(m��o)1(a1, b1) = 1.5/3.0 = 0.5。一般情况下�Q��P代如下进行:(x��)


上面的计���进行�P代,直到 �Q(m��o)n �?�Q(m��o)n-1之间的差别小于一个阈��|��如果计算没有聚合�Q�我们就在�P代超�q�一定次数后停止。上�?的第三副图,���是5�ơ�P代后的结果。表3时一些计���方法,后面的实验表明,C比较好。A叫做 sparce�Q�B叫做 excepted�Q�C叫做verbose
�q���o(h��)
�q�代出的�l�果是一�U�[多匹配]�Q�可能包含有用的匚w��子集�?br /> 三个步骤�Q?br /> 1。用�E�序定义的[限制条�g]�q�行�q���o(h��)�?br /> 2。用双向图中的匹配上下文技术进行过�?br /> 3。比较各�U�技术的有效性(满��用户需求的能力�Q?br /> 限制�Q�主要有两种�Q�一个是[�c�d��]限制�Q�比如只考虑[列]的匹配(匚w��双方都是列)(j��)。第二个�?cardinality 限制�Q�即模式S1中的所有元素都要在S2中有一个映����?br />
stable marriage问题�Q�n奛_��n男配对,不存在这��L(f��ng)��两对 (x; y)�?x0; y0)�Q�其中x喜欢 y0 胜过 y�Q�而且 y0 喜欢 x 胜过 x0。具有stable marriage的匹配结果的total satisfaction可能�?x��)比不具有stable marriage的匹配结果还低!
匚w��质量的评�?br />
基本的评估思想�Q�就是�?用户对匹配结果做的修改越���,匚w��质量���p��高(修改�l�果包括��L��错误的pair�Q�加上正���的pair�Q?br />
from: http://www.cnblogs.com/anf/archive/2006/08/15/477700.html
We are given a set of records. Each record has the same structure, consisting of a number of attribute/value pairs. One of these attributes represents the category of the record. The problem is to determine a decision tree that on the basis of answers to questions about the non-category attributes predicts correctly the value of the category attribute. Usually the category attribute takes only the values {true, false}, or {success, failure}, or something equivalent. In any case, one of its values will mean failure.
For example, we may have the results of measurements taken by experts on some widgets. For each widget we know what is the value for each measurement and what was decided, if to pass, scrap, or repair it. That is, we have a record with as non categorical attributes the measurements, and as categorical attribute the disposition for the widget.
Here is a more detailed example. We are dealing with records reporting on weather conditions for playing golf. The categorical attribute specifies whether or not to Play. The non-categorical attributes are:
ATTRIBUTE | POSSIBLE VALUES ============+======================= outlook | sunny, overcast, rain ------------+----------------------- temperature | continuous ------------+----------------------- humidity | continuous ------------+----------------------- windy | true, false ============+=======================
and the training data is:
OUTLOOK | TEMPERATURE | HUMIDITY | WINDY | PLAY ===================================================== sunny | 85 | 85 | false | Don't Play sunny | 80 | 90 | true | Don't Play overcast| 83 | 78 | false | Play rain | 70 | 96 | false | Play rain | 68 | 80 | false | Play rain | 65 | 70 | true | Don't Play overcast| 64 | 65 | true | Play sunny | 72 | 95 | false | Don't Play sunny | 69 | 70 | false | Play rain | 75 | 80 | false | Play sunny | 75 | 70 | true | Play overcast| 72 | 90 | true | Play overcast| 81 | 75 | false | Play rain | 71 | 80 | true | Don't PlayNotice that in this example two of the attributes have continuous ranges, Temperature and Humidity. ID3 does not directly deal with such cases, though below we examine how it can be extended to do so. A decision tree is important not because it summarizes what we know, i.e. the training set, but because we hope it will classify correctly new cases. Thus when building classification models one should have both training data to build the model and test data to verify how well it actually works.
A simpler example from the stock market involving only discrete ranges has Profit as categorical attribute, with values {up, down}. Its non categorical attributes are:
ATTRIBUTE | POSSIBLE VALUES ============+======================= age | old, midlife, new ------------+----------------------- competition | no, yes ------------+----------------------- type | software, hardware ------------+----------------------- and the training data is: AGE | COMPETITION | TYPE | PROFIT ========================================= old | yes | swr | down --------+-------------+---------+-------- old | no | swr | down --------+-------------+---------+-------- old | no | hwr | down --------+-------------+---------+-------- mid | yes | swr | down --------+-------------+---------+-------- mid | yes | hwr | down --------+-------------+---------+-------- mid | no | hwr | up --------+-------------+---------+-------- mid | no | swr | up --------+-------------+---------+-------- new | yes | swr | up --------+-------------+---------+-------- new | no | hwr | up --------+-------------+---------+-------- new | no | swr | up --------+-------------+---------+--------For a more complex example, here are files that provide records for a series of votes in Congress. The first file describes the structure of the records. The second file provides the Training Set, and the third the Test Set.
The basic ideas behind ID3 are that:
- In the decision tree each node corresponds to a non-categorical attribute and each arc to a possible value of that attribute. A leaf of the tree specifies the expected value of the categorical attribute for the records described by the path from the root to that leaf. [This defines what is a Decision Tree.]
- In the decision tree at each node should be associated the non-categorical attribute which is most informative among the attributes not yet considered in the path from the root. [This establishes what is a "Good" decision tree.]
- Entropy is used to measure how informative is a node. [This defines what we mean by "Good". By the way, this notion was introduced by Claude Shannon in Information Theory.]
Definitions
If there are n equally probable possible messages, then the probability p of each is 1/n and the information conveyed by a message is -log(p) = log(n). [In what follows all logarithms are in base 2.] That is, if there are 16 messages, then log(16) = 4 and we need 4 bits to identify each message.
In general, if we are given a probability distribution P = (p1, p2, .., pn) then the Information conveyed by this distribution, also called the Entropy of P, is:
I(P) = -(p1*log(p1) + p2*log(p2) + .. + pn*log(pn))For example, if P is (0.5, 0.5) then I(P) is 1, if P is (0.67, 0.33) then I(P) is 0.92, if P is (1, 0) then I(P) is 0. [Note that the more uniform is the probability distribution, the greater is its information.]
If a set T of records is partitioned into disjoint exhaustive classes C1, C2, .., Ck on the basis of the value of the categorical attribute, then the information needed to identify the class of an element of T is Info(T) = I(P), where P is the probability distribution of the partition (C1, C2, .., Ck):
P = (|C1|/|T|, |C2|/|T|, ..., |Ck|/|T|)
In our golfing example, we have Info(T) = I(9/14, 5/14) = 0.94,
and in our stock market example we have Info(T) = I(5/10,5/10) = 1.0.
If we first partition T on the basis of the value of a non-categorical attribute X into sets T1, T2, .., Tn then the information needed to identify the class of an element of T becomes the weighted average of the information needed to identify the class of an element of Ti, i.e. the weighted average of Info(Ti):
|Ti| Info(X,T) = Sum for i from 1 to n of ---- * Info(Ti) |T|
In the case of our golfing example, for the attribute Outlook we have
Info(Outlook,T) = 5/14*I(2/5,3/5) + 4/14*I(4/4,0) + 5/14*I(3/5,2/5) = 0.694
Consider the quantity Gain(X,T) defined as
Gain(X,T) = Info(T) - Info(X,T)
This represents the difference between the information needed to identify an element of T and the information needed to identify an element of T after the value of attribute X has been obtained, that is, this is the gain in information due to attribute X.
In our golfing example, for the Outlook attribute the gain is:
Gain(Outlook,T) = Info(T) - Info(Outlook,T) = 0.94 - 0.694 = 0.246.
If we instead consider the attribute Windy, we find that Info(Windy,T) is 0.892 and Gain(Windy,T) is 0.048. Thus Outlook offers a greater informational gain than Windy.
We can use this notion of gain to rank attributes and to build decision trees where at each node is located the attribute with greatest gain among the attributes not yet considered in the path from the root.
The intent of this ordering are twofold:
- To create small decision trees so that records can be identified after only a few questions.
- To match a hoped for minimality of the process represented by the records being considered(Occam's Razor).
The ID3 Algorithm
The ID3 algorithm is used to build a decision tree, given a set of non-categorical attributes C1, C2, .., Cn, the categorical attribute C, and a training set T of records.
function ID3 (R: a set of non-categorical attributes,
C: the categorical attribute,
S: a training set) returns a decision tree;
begin
If S is empty, return a single node with value Failure;
If S consists of records all with the same value for
the categorical attribute,
return a single node with that value;
If R is empty, then return a single node with as value
the most frequent of the values of the categorical attribute
that are found in records of S; [note that then there
will be errors, that is, records that will be improperly
classified];
Let D be the attribute with largest Gain(D,S)
among attributes in R;
Let {dj| j=1,2, .., m} be the values of attribute D;
Let {Sj| j=1,2, .., m} be the subsets of S consisting
respectively of records with value dj for attribute D;
Return a tree with root labeled D and arcs labeled
d1, d2, .., dm going respectively to the trees
ID3(R-{D}, C, S1), ID3(R-{D}, C, S2), .., ID3(R-{D}, C, Sm);
end ID3;
In the Golfing example we obtain the following decision tree:
Outlook
/ | \
/ | \
overcast / |sunny \rain
/ | \
Play Humidity Windy
/ | | \
/ | | \
<=75 / >75| true| \false
/ | | \
Play Don'tPlay Don'tPlay Play
In the stock market case the decision tree is:
Age
/ | \
/ | \
new/ |mid \old
/ | \
Up Competition Down
/ \
/ \
no/ \yes
/ \
Up Down
Here is the decision tree, just as produced by c4.5, for the voting example introduced earlier.
In building a decision tree we can deal with training sets that have records with unknown attribute values by evaluating the gain, or the gain ratio, for an attribute by considering only the records where that attribute is defined.
In using a decision tree, we can classify records that have unknown attribute values by estimating the probability of the various possible results. In our golfing example, if we are given a new record for which the outlook is sunny and the humidity is unknown, we proceed as follows:
We can deal with the case of attributes with continuous ranges as follows. Say that attribute Ci has a continuous range. We examine the values for this attribute in the training set. Say they are, in increasing order, A1, A2, .., Am. Then for each value Aj, j=1,2,..m, we partition the records into those that have Ci values up to and including Aj, and those that have values greater than Aj. For each of these partitions we compute the gain, or gain ratio, and choose the partition that maximizes the gain. Pruning of the decision tree is done by replacing a whole subtree by a leaf node. The replacement takes place if a decision rule establishes that the expected error rate in the subtree is greater than in the single leaf. For example, if the simple decision tree
is obtained with one training red success record and two training blue Failures, and then in the Test set we find three red failures and one blue success, we might consider replacing this subtree by a single Failure node. After replacement we will have only two errors instead of five failures.
Winston shows how to use Fisher's exact test to determine if the category attribute is truly dependent on a non-categorical attribute. If it is not, then the non-categorical attribute need not appear in the current path of the decision tree.
Quinlan and Breiman suggest more sophisticated pruning heuristics.
It is easy to derive a rule set from a decision tree: write a rule for each path in the decision tree from the root to a leaf. In that rule the left-hand side is easily built from the label of the nodes and the labels of the arcs.
The resulting rules set can be simplified:
Let LHS be the left hand side of a rule. Let LHS' be obtained from LHS by eliminating some of its conditions. We can certainly replace LHS by LHS' in this rule if the subsets of the training set that satisfy respectively LHS and LHS' are equal.
A rule may be eliminated by using metaconditions such as "if no other rule applies".
Using Gain Ratios
The notion of Gain introduced earlier tends to favor attributes that have a large number of values. For example, if we have an attribute D that has a distinct value for each record, then Info(D,T) is 0, thus Gain(D,T) is maximal. To compensate for this Quinlan suggests using the following ratio instead of Gain:
Gain(D,T)
GainRatio(D,T) = ----------
SplitInfo(D,T)
where SplitInfo(D,T) is the information due to the split of T on the basis
of the value of the categorical attribute D. Thus SplitInfo(D,T) is
I(|T1|/|T|, |T2|/|T|, .., |Tm|/|T|)
where {T1, T2, .. Tm} is the partition of T induced by the value of D.
In the case of our golfing example SplitInfo(Outlook,T) is
-5/14*log(5/14) - 4/14*log(4/14) - 5/14*log(5/14) = 1.577
thus the GainRatio of Outlook is 0.246/1.577 = 0.156. And
SplitInfo(Windy,T) is
-6/14*log(6/14) - 8/14*log(8/14) = 6/14*0.1.222 + 8/14*0.807
= 0.985
thus the GainRatio of Windy is 0.048/0.985 = 0.049
You can run PAIL to see how ID3 generates the decision tree [you need to have an X-server and to allow access (xhost) from yoda.cis.temple.edu].
C4.5 Extensions
C4.5 introduces a number of extensions of the original ID3 algorithm.
We move from the Outlook root node to the Humidity node following
the arc labeled 'sunny'. At that point since we do not know
the value of Humidity we observe that if the humidity is at most 75
there are two records where one plays, and if the humidity is over
75 there are three records where one does not play. Thus one
can give as answer for the record the probabilities
(0.4, 0.6) to play or not to play.
In our Golfing example, for humidity, if T is the training set, we determine the information for each partition and find the best partition at 75. Then the range for this attribute becomes {<=75, >75}. Notice that this method involves a substantial number of computations.
Pruning Decision Trees and Deriving Rule Sets
The decision tree built using the training set, because of the way it was built, deals correctly with most of the records in the training set. In fact, in order to do so, it may become quite complex, with long and very uneven paths.
Color
/ \
red/ \blue
/ \
Success Failure
You can run the C45 program here [you need to have an X-server and to allow access (xhost) from yoda.cis.temple.edu].
Classification Models in the Undergraduate AI Course
It is easy to find implementations of ID3. For example, a Prolog program by Shoham and a nice Pailmodule.
The software for C4.5 can be obtained with Quinlan's book. A wide variety of training and test data is available, some provided by Quinlan, some at specialized sites such as the University of California at Irvine.
Student projects may involve the implementation of these algorithms. More interesting is for students to collect or find a significant data set, partition it into training and test sets, determine a decision tree, simplify it, determine the corresponding rule set, and simplify the rule set.
The study of methods to evaluate the error performance of a decision tree is probably too advanced for most undergraduate courses.
Breiman,Friedman,Olshen,Stone: Classification and Decision Trees Wadsworth, 1984 A decision science perspective on decision trees. Quinlan,J.R.: C4.5: Programs for Machine Learning Morgan Kauffman, 1993 Quinlan is a very readable, thorough book, with actual usable programs that are available on the internet. Also available are a number of interesting data sets. Quinlan,J.R.: Simplifying decision trees International Journal of Man-Machine Studies, 27, 221-234, 1987 Winston,P.H.: Artificial Intelligence, Third Edition Addison-Wesley, 1992 Excellent introduction to ID3 and its use in building decision trees and, from them, rule sets.
ingargiola@cis.temple.edu
from: http://www.cis.temple.edu/~ingargio/cis587/readings/id3-c45.html
什么是计算与计���的�c�d��
在大众的意识里,计算首先指的���是数的加减乘除�Q�其�ơ则为方�E�的求解、函数的微分�U�分�{�;懂的多一点的人知道,计算在本质上�q�包括定理的证明推导。可以说�Q�“计���”是一个无��Z��知元��Z��晓的数学概念�Q�但是,真正能够回答计算的本质是什么的人恐怕不多。事实上�Q�直�?930�q�代�Q�由于哥德尔�Q�K.Godel�Q?906-1978�Q�、丘�?A.Church�Q?903-1995)、图�?A.M.TUI-ing�Q?912-1954)�{�数学家的工作,��Z��才弄清楚什么是计算的本质,以及(qi��ng)什么是可计���的、什么是不可计算的等�Ҏ(gu��)��性问题�?/FONT>
抽象地说�Q�所谓计���,���是从一个符号串f变换成另一个符号串g。比如说,从符号串12+3变换�?5���是一个加法计���。如果符号串f�?IMG height=15 src="http://cfc.nankai.edu.cn/readings/image/lijie/1.jpg" width=15>�Q�而符号串g�?x,从f到g的计���就是微分。定理证明也是如此,令f表示一�l�公理和推导规则�Q���o(h��)g是一个定�?那么从f到g的一�p�d��变换���是定理g的证明。从�q�个角度看,文字���译也是计算�Q�如f代表一个英文句子,而g为含意相同的中文句子�Q�那么从f到g���是把英文翻译成中文。这些变换间有什么共同点�Q��ؓ(f��)什么把它们都叫做计���?因�ؓ(f��)它们都是从己知符�?�?开始,一步一步地改变�W�号(�?�Q�经�q�有限步骤,最后得��C��个满���预先规定的�W�号(�?的变换过�E��?/FONT>
从类型上�Ԍ��计算主要有两大类�Q�数��D�����和�W�号推导。数��D�����包括实数和函数的加减乘除、幕�q�算、开方运���、方�E�的求解�{�。符��h��导包括代��C��各种函数的恒�{�式、不�{�式的证�?几何命题的证明等。但无论是数��D�����还是符��h���?它们在本质上是等��L(f��ng)��、一致的�Q�即二者是密切兌���的,可以�怺�转化�Q�具有共同的计算本质。随着数学的不断发�?�q�可能出现新的计���类型�?/FONT>
计算的实质与E奇-囄���论点
��Z��(ji��n)回答�I�竟什么是计算、什么是可计���性等问题�Q��h们采取的是徏立计���模型的�Ҏ(gu��)��。从20世纪30�q�代�?0�q�代�Q�数理逻辑学家相��提出�?ji��n)四�U�模型,它们是一般递归函数、��d��计算函数、图灉|��和�L斯特(E.L.Post�Q?897-1954)�pȝ��。这�U�种模型完全从不同的角度探究计算�q�程或证明过�E�,表面上看区别很大�Q�但事实上却是等��L(f��ng)���Q�即它们完全��h��一��L(f��ng)��计算能力D在这一事实基础上,最�l��Ş成了(ji��n)如今著名的丘�?囄���论点�Q�凡是可计算的函数都是一般递归函数(或是囄���机可计算函数�{?。这���q��立了(ji��n)计算与可计算性的数学含义。下面主要对一般递归函数作一���要介�l��?/FONT>
哥�d��?d��ng)首先�?931�q�提��Z��(ji��n)原始递归函数的概��c(di��n)��所谓原始递归函数,���是由初始函数出发,�l�过有限�ơ的使用代�h与原始递归式而做出的函数。这里所说的初始函数是指下列三种函数�Q?/FONT>
(1) 零函�?(x)=0(函数值恒为零)�Q?/FONT>
(2) ���媄(ji��ng)函数![]() (x1,x2,�?xn)=xi(1≤i≤n)(函数的��g���W�i个自变元的值相�?�Q?/FONT>
(x1,x2,�?xn)=xi(1≤i≤n)(函数的��g���W�i个自变元的值相�?�Q?/FONT>
后��函数S(x)=x+1(其��gؓ(f��)x的直接后�l�数)�?/FONT>
代�h与原始递归式是构造新函数的算子�?/FONT>
代�h(又名叠置、�P�|?�Q�它是最���单又最重要的算�?其一般�Ş式是:�׃��个m元函数f与m个n元函数g1�Q�g2�Q�…,gm造成新函数f(g1(x1,x2,�?xn),g2(x1,x2,�?xn),�?gm(x1,x2,�?xn))�?/FONT>
原始递归式,其一般�Ş式�ؓ(f��)

�Ҏ(gu��)����Cؓ(f��)

其特�Ҏ(gu��)���Q�不能由g,h两已知函数直接计���新函数的一般值f(u,x),而只能依�ơ计���f(u,0)�Q�f(u,1)�Q�f(u,2)�Q�…;但只要依�ơ计���,必能把�Q何一个f(u,x)�Q�对值都���出来。换句话��_(d��)��只要g,h有定义且可计���,则新函数f也有定义且可计算�?/FONT>
�Ҏ(gu��)��埃尔布朗(J.Herbrand�Q?908-1931)一���信的暗�C�,哥�d��?d��ng)�?934�q�引�q�了(ji��n)一般递归函数的概��c(di��n)��后�l�克�?S.C.Kleene�Q?909-1994)的改�q�与阐明�Q�便出现�?ji��n)现在普遍采用的定义。所谓一般递归函数�Q�就是由初始函数出发�Q�经�q�有限次使用代�h、原始递归式和μ���子而做成的有定义的函数�?�q�里的μ算子就是造逆函数的���子或求根算子�?/FONT>
 如此定义的一般递归函数比原始递归函数更广�Q�这是没有�Q何疑问的。但是,��Z���q�是可以问:(x��)�q�样定义的函数是否已�l�包括了(ji��n)所有直观上的可计算函数�Q�如果还有更�q�的可计���函数又该怎样定义�Q�在受到�q�类问题困惑的同�Ӟ��丘奇、克林又提出�?ji��n)一�c�d��计算函数�Q�叫做��d��计算函数。但事隔不久�Q�丘奇和克林便分别证明了(ji��n)λ可计���函数正好就是一般递归函数�Q�即�q�两�c�d��计算函数是等��L(f��ng)��、一致的。在�q�一有力的证据基���上,丘奇�?936�q�公开发表�?ji��n)他早在两年前就孕育�q�的一个论点,卌���名的丘奇论点�Q�每个能行地可计���的函数都是一般递归函数�?/FONT>
如此定义的一般递归函数比原始递归函数更广�Q�这是没有�Q何疑问的。但是,��Z���q�是可以问:(x��)�q�样定义的函数是否已�l�包括了(ji��n)所有直观上的可计算函数�Q�如果还有更�q�的可计���函数又该怎样定义�Q�在受到�q�类问题困惑的同�Ӟ��丘奇、克林又提出�?ji��n)一�c�d��计算函数�Q�叫做��d��计算函数。但事隔不久�Q�丘奇和克林便分别证明了(ji��n)λ可计���函数正好就是一般递归函数�Q�即�q�两�c�d��计算函数是等��L(f��ng)��、一致的。在�q�一有力的证据基���上,丘奇�?936�q�公开发表�?ji��n)他早在两年前就孕育�q�的一个论点,卌���名的丘奇论点�Q�每个能行地可计���的函数都是一般递归函数�?/FONT>
与此同时�Q�图灵定义了(ji��n)另一�c�d��计算函数�Q�叫做图灉|��可计���性函�?�q�且提出�?ji��n)著名的囄���论点�Q�能行可计算函数都是用图灉|��可计���的函数。图灉|��是图灉|��出的一�U�计���模型,或一台理��������机口它可以说是对�h�c�计���与机器计算的最一般、最高度的抽象。一�q�后�Q�图灵进一步证明了(ji��n)囄���机可计算函数与��d��定义函数是一致的�Q�当然也���和一般递归函数一致、等仗���于是,表面上不同的三类可计���函数在本质上就是一�c�R��这样一来,丘奇论点和图灵论点也���是一回事�?ji��n),现将它们合称��Z���?囄���论点�Q�即直观的能行可计算函数�{�同于一般递归函数、可λ定义函数和图灉|��可计���函数�?/FONT>
丘奇�Q�图灵论点的提出�Q�标志着人类对可计算函数与计���本质的认识辑ֈ��?ji��n)空前的高度�Q�它是数学史上一块夺目的里程����?/FONT>
一般递归函数比较抽象�Q��ؓ(f��)此给��Z���U�较为直观的解释。大家知道,凡能够计���的�Q�即使是“心(j��)���”,��d��以把其计���过�E�记录下来,而且是逐个步骤逐个步骤地记录下来。所谓计���过�E�,是指从初始符��h��已知�W�号开始,一步一步地改变(变换)�W�号�Q�最后得��C��个满���预先规定的条�g的符��P���q�从该符��h��照一定方法得到所求结果,��x��求函数的值的全过�E�。可如此计算的函敎ͼ�一般称为可以在有限步骤内计���的函数。现已证明:(x��)凡是可以从某些初始符号开始,而在有限步骤内计���的函数都是递归函数。由此可以看刎ͼ�“能够记录下来”便�W�合�?ji��n)可计算性或递归性的本质要求。一般递归函数的实质也由此昑־�十分直观易懂�?/FONT>
丘奇�Q�图灵论点的提出与确认,在数学和计算机科学上��h��重大的理论和现实意义。正如我国数理逻辑专家莫绍揆教授所�a��Q�有�?ji��n)这个论点以后,���可以断定某些问题是不能能行地解��x��不能能行地判定的。对于计���机�U�学�Q�丘�?囄���论点的意义在于它明确�ȝ���?ji��n)计���机的本质或计算机的计算能力�Q�确定了(ji��n)计算机只能计���一般递归函数�Q�对于一般递归函数之外的函敎ͼ�计算机是无法计算的�?/FONT>
DNA计算:新型计算方式的出�?/FONT>
1994�q?1月,���国计算机科学家阿�d勒曼(L.Adleman)在美国《科学》上公布DNA计算机的理论�Q��ƈ成功�q�用DNA计算�����决了(ji��n)一个有向哈密顿路径问题�?DNA计算机的提出�Q���生于�q�样一个发玎ͼ�即生物与数学的相似性:(x��)(1)生物体异常复杂的�l�构是对由DNA序列表示的初始信息执行简单操�?复制、剪�?的结果;(2)可计���函数f(ω)的结果可以通过在ω上执行一�p�d��基本的简单函数而获得�?/FONT>
阿�d勒曼不仅意识到这两个�q�程的相似性,而且意识到可以利用生物过�E�来模拟数学�q�程。更���切地说是,DNA串可用于表示信息�Q�酶可用于模拟简单的计算。这是因为:(x��)首先�Q�DNA是由�U�C��核昔酸的一些单元组成,�q�些核昔酔R��着附在其上的化学组或基的不同而不同。共有四�U�基�Q�腺嘌呤、鸟嘌呤、胞(y��u)嘧啶和胸腺嘧�Ӟ��分别用A、G、C、T表示。单链DNA可以看作是由�W�号A、G、C、T�l�成的字�W�串。从数学上讲�Q�这意味着可以用一个含有四个字�W�的字符集∑ =A、G、C、T来�ؓ(f��)信息�~�码(�?sh��)子计算��Z��使用0�?�q�两个数�?。其�ơ,DNA序列上的一些简单操作需要酶的协助,不同的酶发挥不同的作用。�v作用的有四种�Ӟ��(x��)限制性内切酶�Q�主要功能是切开包含限制性位点的双链DNA�Q�DNA�q�接�?它主要是把一个DNA铄���端点同另一个链�q�接在一��P��DNA聚合�?它的功能包括DNA的复制与�?j��)进DNA的合成;外切�Ӟ��它可以有选择地破坏双链或单链DNA分子。正是基于这四种酶的协作实现�?ji��n)DNA计算�?/FONT>
不过�Q�目前DNA计算�����够处理的问题�Q�还仅仅是利用分子技术解决的几个特定问题�Q�属一�ơ性实验。DNA计算�����没有一个固定的�E�式。由于问题的多样性,��D��所采用的分子生物学技术的多样性,具体问题需要设计具体的实验�Ҏ(gu��)��口这便引��Z��(ji��n)两个�Ҏ(gu��)��性问�?也是阿�d勒曼最早意识到�?�Q?1)DNA计算机可以解军_��些问题确切地��_(d��)��DNA计算机是完备的吗�Q�即通过操纵DNA能完成所有的(囄����?可计���函数吗�Q?2)是否可设计出可编�E�序的DNA计算机?��x��否存在类��g���?sh��)子计算机的通用计算模型——图灉|��——那��L(f��ng)��通用DNA�pȝ��(模型)�Q�目前,��Z��正处在对�q�两个根本性问题的研究�q�程之中口在�W�者看来,�q�就�c�M��于在�?sh��)子计算�����生之前�?0世纪三四十年代理��������机的研�I�����D�c(di��n)��如今,已经提出�?ji��n)多�U�DNA计算模型�Q�但各有千秋�Q�公认的DNA计算机的“图灉|��”还没有诞生。相对而言�Q�一�U�被�U�Cؓ(f��)“剪接系�l�”的DNA计算机模型较为成功�?/FONT>
有了(ji��n)“剪接系�l�”这个DNA计算机的数学模型后,便可以来回答前面提出的DNA计算的完备性与通用性问题。前面讲�q�,丘奇-囄���论点深刻地刻��M��(ji��n)��M��实际计算机的计算能力——�Q何可计算函数都是可由囄�����������的函数(一般递归函数)。现已证明:(x��)剪接�pȝ��是计���完备的�Q�即��M��可计���函数都可用剪接�pȝ��来计���D反之亦然。这���回�{�了(ji��n)DNA计算机可以解军_��些问题——全部图灉|��可计���问题。至于是否存在基于剪接的可编�E�计���机�Q�也有了(ji��n)肯定的答案:(x��)�Ҏ(gu��)��个给定的字符集T�Q�都存在一个剪接系�l�,其公理集和规则集都是有限的,而且对于以T为终�l�字�W�集的一�cȝ���l�是通用的。这���是��_(d��)��理论上存在一个基于剪接操作的通用可编�E�的DNA计算机。这些计���机使用的生物操作只有合成、剪�?切割-�q�接)和抽取�?/FONT>
DNA计算机理论的出现意味着计算方式的重大变革。当�?d��ng)���引�v计算方式重大变革的远不止DNA计算机,光学计算机、量子计���机、蛋白质计算机等新型计算机模型层��Z���I�P��它们使原有的计算方式发生�?ji��n)前所未有的变化�?/FONT>
计算方式�?qi��ng)其演�?/FONT>
���单地�Ԍ��所谓计���方式就是符号变换的操作方式�Q�尤其指最基本的动作方式。广义地�Ԍ���q�应包括�W�号的蝲体或�W�号的外在表现�Ş式,亦即信息的表征或表达。比如,中国古代的筹���,���是用一�l�竹���表征的计算方式�Q�后来的珠算则是用算盘或���珠表征的计���方式,再后来的�W�算又是一�U�用文字�W�号表征的计���方式,�q�一�p�d��计算方式的变化,表现��������方式的多样性与不断�q�化的趋�ѝ��相对于后来出现的机器计���方式,上述各种计算方式均可归结为“手工计���方式”,其特�Ҏ(gu��)��用手工操作符��P��实施�W�号的变换�?/FONT>
不过�Q�真正具有革命性的计算方式�Q�还是随着�?sh��)子计算机的产生才出现的。机器计���的历史可以�q�溯�?641�q�_(d��)��当年18岁的法国数学家帕斯卡从机械时钟得到启�C�:(x��)齿轮也能计数�Q�于是成功地制作�?ji��n)一台��轮传动的八位加法计算机口�q���人类计算方式、计���技术进入了(ji��n)一个新的阶�D�c(di��n)��后来经�q��h们数癑ֹ�的艰辛努力,�l�于�?945�q�成功研制出�?ji��n)世界上�W�一台电(sh��)子计���机。从此,人类�q�入�?ji��n)一个全新的计算技术时代�?/FONT>
从最早的帕斯卡��轮机��C��天最先进的电(sh��)子计���机�Q�计���机已经历了(ji��n)四大发展时期。计���技术有�?ji��n)长���的发展。这时计���表��Cؓ(f��)一�U�物理性质的机械的操作�q�程。符号不再是用竹���、算珠、字母表征,而是用��轮表征,用电(sh��)���表征,用电(sh��)压表征等�{�。但是,无论是手工计���还是机器计���,其计���方式——操作的基本动作都是一�U�物理性质的符号变�?具体是由“加”“减”这�U�基本动作构�?。二者的区别在于�Q�前者是手工的,�q�算速度比较慢;后者则是自动的�Q�运���速度极快�?/FONT>
如今出现的DNA计算无疑有着更大的本质性变化,计算不再是一�U�物理性质的符号变换,而是一�U�化学性质的符号变换,即不再是物理性质的“加”“减”操作,而是化学性质的切割和�_�脓(chu��ng)、插人和删除。这�U�计���方式将��d��改变计算机硬件的性质�Q�改变计���机基本的运作方式,其意义将是极为深�q�的。阿德勒曼在提出DNA计算机的时候就�怿��Q�DNA计算机所蕴涵的理念可使计���的方式产生�q�化�?/FONT>
量子计算机在理论上的出现�Q���计算方式的进化又有了(ji��n)新的可能。电(sh��)子计���机的理论模型是�l�典的通用囄���机——一�U�确定型囄���机,量子计算机的理论模型——量子图灉|��则是一�U�概率型囄���机。直观一些说�Q�传�l�电(sh��)脑是通过���芯片上微型晶体���电(sh��)位的“开”和“关”状态来表达二进位制�?�?�Q�从而进行信息数据的处理和储存。每个电(sh��)位只能处理一个数据,�?�?�Q�许多个�?sh��)位依次串连��h���Q�才能共同完成一�ơ复杂的�q�算。这�U�线性计���方式遵循普通的物理学原则,��h��明显的局限性。而量子计���机的运���方式则建立在原子运动的层面上,�H�破�?ji��n)分子物理的界限。根据量子论原理�Q�原子具有在同一时刻处于两个不同位置、又同时向上下两个相反方向旋转的�Ҏ(gu��)��,�U�Cؓ(f��)“量子超态”。而一旦有外力�q�扰�Q�模�p�运动的原子又可以马上归于准���的定位。这�U�似是而非的�沌状态与��Z��熟知的常规世界相矛盾�Q�但如果利用其表达信息,却能发挥出其瞬息之间千变万化而又万变不离其宗的神奇功效。因为当许多个量子状态的原子�U�缠在一��h���Q�它们又因量子位的“叠加性”,可以同时一起展开“�ƈ行计���”,从而��其具备超高速的�q�算能力。电(sh��)子线性计���方式如同万只蜗牛排队过独木桥,而量子�ƈ行运���好比万只飞鸟同时升上天�I��?/FONT>
计算方式演变的意�?/FONT>
计算方式的不断进化有着十分重要的理论意义和现实意义�Q�笔者认��������表明以下两斚w��。其一�Q�计���方式是一�U�历史的�l�果�Q�而非计算本性的逻辑必然。加拿大的卡�?L.Kari)指出�Q�“DNA计算是考察计算问题的一�U�全新方式。或许这正是大自然做数学的方法:(x��)不是用加和减�Q�而是用切割和�_�脓(chu��ng)、用插入和删除。正如用十进制计数是因�ؓ(f��)我们有十个手指那��P��或许我们目前计算中的基本功能仅因��Z�h�c�d��史��然。正如�h们已�l�采用其他进制计��C����P��或许现在是考虑其他的计���方式的时候了(ji��n)。”笔者以为,�q�一说法是很有启�C�性的。确实,仔细回顾一下�h�c�计���方式或计算技术的历史,��׃��难体�?x��)到计算方式是一�U�历史的�l�果�Q�而非计算本性的逻辑必然�?/FONT>
也就是说�Q�计���之所以�ؓ(f��)计算�Q�在于它��h��一�U�根本的递归性,或在于它是一�U�可一步一步进行的�W�号串变换操作。至于这�U�符号变换的操作方式如何�Q�以�?qi��ng)符��L(f��ng)��载体或其外在表现形式如何�Q�都不是本质性的东西�Q�它们元不是一�U�历史的�l�果�Q�无不处于一�U�不断变革或�q�化的过�E�之中。不同表征下的符号变换有着不同的操作方式,甚至同一�U�表征下的符号变换都可以有不同的操作方式�Q�既可以是物理性的方式�Q�也可以是化学性的方式�Q�即可以是经典的方式,也可以是量子的方式;既可以是���定性的方式�Q�也可以是概率性的方式。在此,计算本质的统一性与计算方式的多��h��得��C��(ji��n)深刻的体现。笔者相信,DNA计算机、量子计���机�{�的出现已经打开�?ji��n)�h们畅��x��来计���方式的思维视窗�Q�随着�U�学技术的不断发展�Q�计���方式的多样性还�?x��)有新的表现�?/FONT>
其二�Q�计���方式的历史性、多��h��反观了(ji��n)计算本性的逻辑必然性、统一性。由丘奇-囄���论点所揭示的计���本质是非常普适的�Q�它不仅包括数��D�����、定理推导等不同形式的计���,而且包括�����、电(sh��)子计���机�{�不同“计���器”的计算。大家不要忘�?ji��n),以丘�?囄���论点为基石的可计���性理论是在电(sh��)子计���机诞生之前�?930�q�代提出的,卛_���q����在对�?sh��)子计算�����行�ȝ��与抽象的基础上提出,但又深刻地刻��M��(ji��n)�?sh��)子计算机的计算本质。如今最先进的电(sh��)子计���机在本质上���是一台图灉|���Q�或者凡是计���机可计���的函数都是一般递归函数。现在�h们又�q�一步认识到�Q�目前尚在实验室阶段的DNA计算机、量子计���机�Q�在本质上也是一�U�图灵计���。这说明不同形式的计���、不同“计���器”的计算�Q�在计算本质上是一致的�Q�这���是递归计算或图灵计����?BR>
转自�Q?A >http://cfc.nankai.edu.cn/readings/lijie.htm