1.1、摘要

      貝葉斯分類是一類分類算法的總稱，這類算法均以貝葉斯定理為基礎(chǔ)，故統(tǒng)稱為貝葉斯分類。本文作為分類算法的第一篇，將首先介紹分類問題，對(duì)分類問題進(jìn)行一個(gè)正式的定義。然后，介紹貝葉斯分類算法的基礎(chǔ)——貝葉斯定理。最后，通過實(shí)例討論貝葉斯分類中最簡(jiǎn)單的一種：樸素貝葉斯分類。

1.2、分類問題綜述

      對(duì)于分類問題，其實(shí)誰都不會(huì)陌生，說我們每個(gè)人每天都在執(zhí)行分類操作一點(diǎn)都不夸張，只是我們沒有意識(shí)到罷了。例如，當(dāng)你看到一個(gè)陌生人，你的腦子下意識(shí)判斷TA是男是女；你可能經(jīng)常會(huì)走在路上對(duì)身旁的朋友說“這個(gè)人一看就很有錢、那邊有個(gè)非主流”之類的話，其實(shí)這就是一種分類操作。

      從數(shù)學(xué)角度來說，分類問題可做如下定義：

      已知集合：和，確定映射規(guī)則，使得任意有且僅有一個(gè)使得成立。（不考慮模糊數(shù)學(xué)里的模糊集情況）

      其中C叫做類別集合，其中每一個(gè)元素是一個(gè)類別，而I叫做項(xiàng)集合，其中每一個(gè)元素是一個(gè)待分類項(xiàng)，f叫做分類器。分類算法的任務(wù)就是構(gòu)造分類器f。

      這里要著重強(qiáng)調(diào)，分類問題往往采用經(jīng)驗(yàn)性方法構(gòu)造映射規(guī)則，即一般情況下的分類問題缺少足夠的信息來構(gòu)造100%正確的映射規(guī)則，而是通過對(duì)經(jīng)驗(yàn)數(shù)據(jù)的學(xué)習(xí)從而實(shí)現(xiàn)一定概率意義上正確的分類，因此所訓(xùn)練出的分類器并不是一定能將每個(gè)待分類項(xiàng)準(zhǔn)確映射到其分類，分類器的質(zhì)量與分類器構(gòu)造方法、待分類數(shù)據(jù)的特性以及訓(xùn)練樣本數(shù)量等諸多因素有關(guān)。

      例如，醫(yī)生對(duì)病人進(jìn)行診斷就是一個(gè)典型的分類過程，任何一個(gè)醫(yī)生都無法直接看到病人的病情，只能觀察病人表現(xiàn)出的癥狀和各種化驗(yàn)檢測(cè)數(shù)據(jù)來推斷病情，這時(shí)醫(yī)生就好比一個(gè)分類器，而這個(gè)醫(yī)生診斷的準(zhǔn)確率，與他當(dāng)初受到的教育方式（構(gòu)造方法）、病人的癥狀是否突出（待分類數(shù)據(jù)的特性）以及醫(yī)生的經(jīng)驗(yàn)多少（訓(xùn)練樣本數(shù)量）都有密切關(guān)系。

1.3、貝葉斯分類的基礎(chǔ)——貝葉斯定理

      每次提到貝葉斯定理，我心中的崇敬之情都油然而生，倒不是因?yàn)檫@個(gè)定理多高深，而是因?yàn)樗貏e有用。這個(gè)定理解決了現(xiàn)實(shí)生活里經(jīng)常遇到的問題：已知某條件概率，如何得到兩個(gè)事件交換后的概率，也就是在已知P(A|B)的情況下如何求得P(B|A)。這里先解釋什么是條件概率：

      表示事件B已經(jīng)發(fā)生的前提下，事件A發(fā)生的概率，叫做事件B發(fā)生下事件A的條件概率。其基本求解公式為：。

      貝葉斯定理之所以有用，是因?yàn)槲覀冊(cè)谏钪薪?jīng)常遇到這種情況：我們可以很容易直接得出P(A|B)，P(B|A)則很難直接得出，但我們更關(guān)心P(B|A)，貝葉斯定理就為我們打通從P(A|B)獲得P(B|A)的道路。

      下面不加證明地直接給出貝葉斯定理：

      

1.4、樸素貝葉斯分類

1.4.1、樸素貝葉斯分類的原理與流程

      樸素貝葉斯分類是一種十分簡(jiǎn)單的分類算法，叫它樸素貝葉斯分類是因?yàn)檫@種方法的思想真的很樸素，樸素貝葉斯的思想基礎(chǔ)是這樣的：對(duì)于給出的待分類項(xiàng)，求解在此項(xiàng)出現(xiàn)的條件下各個(gè)類別出現(xiàn)的概率，哪個(gè)最大，就認(rèn)為此待分類項(xiàng)屬于哪個(gè)類別。通俗來說，就好比這么個(gè)道理，你在街上看到一個(gè)黑人，我問你你猜這哥們哪里來的，你十有八九猜非洲。為什么呢？因?yàn)楹谌酥蟹侵奕说谋嚷首罡撸?dāng)然人家也可能是美洲人或亞洲人，但在沒有其它可用信息下，我們會(huì)選擇條件概率最大的類別，這就是樸素貝葉斯的思想基礎(chǔ)。

      樸素貝葉斯分類的正式定義如下：

      1、設(shè)為一個(gè)待分類項(xiàng)，而每個(gè)a為x的一個(gè)特征屬性。

      2、有類別集合。

      3、計(jì)算。

      4、如果，則。

      那么現(xiàn)在的關(guān)鍵就是如何計(jì)算第3步中的各個(gè)條件概率。我們可以這么做：

      1、找到一個(gè)已知分類的待分類項(xiàng)集合，這個(gè)集合叫做訓(xùn)練樣本集。

      2、統(tǒng)計(jì)得到在各類別下各個(gè)特征屬性的條件概率估計(jì)。即。

      3、如果各個(gè)特征屬性是條件獨(dú)立的，則根據(jù)貝葉斯定理有如下推導(dǎo)：

      

      因?yàn)榉帜笇?duì)于所有類別為常數(shù)，因?yàn)槲覀冎灰獙⒎肿幼畲蠡钥伞Ｓ忠驗(yàn)楦魈卣鲗傩允菞l件獨(dú)立的，所以有：

      

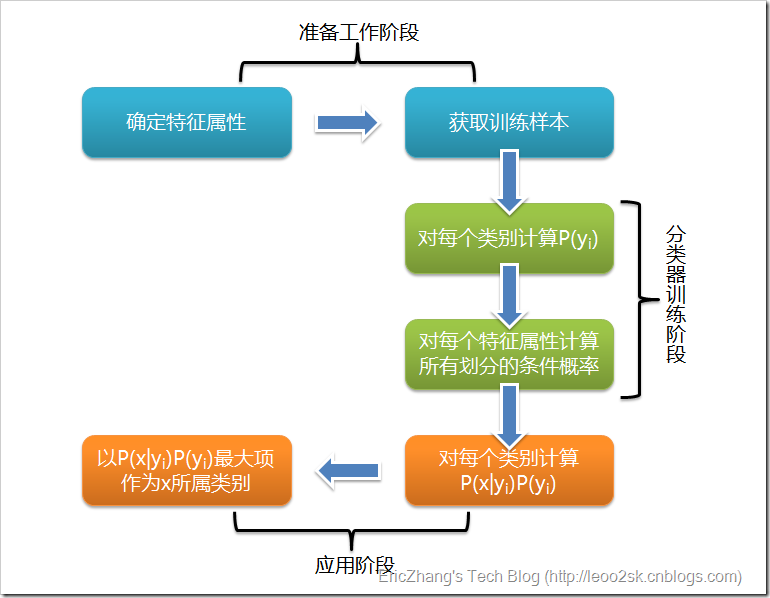
      根據(jù)上述分析，樸素貝葉斯分類的流程可以由下圖表示（暫時(shí)不考慮驗(yàn)證）：

      可以看到，整個(gè)樸素貝葉斯分類分為三個(gè)階段：

      第一階段——準(zhǔn)備工作階段，這個(gè)階段的任務(wù)是為樸素貝葉斯分類做必要的準(zhǔn)備，主要工作是根據(jù)具體情況確定特征屬性，并對(duì)每個(gè)特征屬性進(jìn)行適當(dāng)劃分，然后由人工對(duì)一部分待分類項(xiàng)進(jìn)行分類，形成訓(xùn)練樣本集合。這一階段的輸入是所有待分類數(shù)據(jù)，輸出是特征屬性和訓(xùn)練樣本。這一階段是整個(gè)樸素貝葉斯分類中唯一需要人工完成的階段，其質(zhì)量對(duì)整個(gè)過程將有重要影響，分類器的質(zhì)量很大程度上由特征屬性、特征屬性劃分及訓(xùn)練樣本質(zhì)量決定。

      第二階段——分類器訓(xùn)練階段，這個(gè)階段的任務(wù)就是生成分類器，主要工作是計(jì)算每個(gè)類別在訓(xùn)練樣本中的出現(xiàn)頻率及每個(gè)特征屬性劃分對(duì)每個(gè)類別的條件概率估計(jì)，并將結(jié)果記錄。其輸入是特征屬性和訓(xùn)練樣本，輸出是分類器。這一階段是機(jī)械性階段，根據(jù)前面討論的公式可以由程序自動(dòng)計(jì)算完成。

      第三階段——應(yīng)用階段。這個(gè)階段的任務(wù)是使用分類器對(duì)待分類項(xiàng)進(jìn)行分類，其輸入是分類器和待分類項(xiàng)，輸出是待分類項(xiàng)與類別的映射關(guān)系。這一階段也是機(jī)械性階段，由程序完成。

1.4.2、估計(jì)類別下特征屬性劃分的條件概率及Laplace校準(zhǔn)

      這一節(jié)討論P(yáng)(a|y)的估計(jì)。

      由上文看出，計(jì)算各個(gè)劃分的條件概率P(a|y)是樸素貝葉斯分類的關(guān)鍵性步驟，當(dāng)特征屬性為離散值時(shí)，只要很方便的統(tǒng)計(jì)訓(xùn)練樣本中各個(gè)劃分在每個(gè)類別中出現(xiàn)的頻率即可用來估計(jì)P(a|y)，下面重點(diǎn)討論特征屬性是連續(xù)值的情況。

      當(dāng)特征屬性為連續(xù)值時(shí)，通常假定其值服從高斯分布（也稱正態(tài)分布）。即：

      

      而

      因此只要計(jì)算出訓(xùn)練樣本中各個(gè)類別中此特征項(xiàng)劃分的各均值和標(biāo)準(zhǔn)差，代入上述公式即可得到需要的估計(jì)值。均值與標(biāo)準(zhǔn)差的計(jì)算在此不再贅述。

      另一個(gè)需要討論的問題就是當(dāng)P(a|y)=0怎么辦，當(dāng)某個(gè)類別下某個(gè)特征項(xiàng)劃分沒有出現(xiàn)時(shí)，就是產(chǎn)生這種現(xiàn)象，這會(huì)令分類器質(zhì)量大大降低。為了解決這個(gè)問題，我們引入Laplace校準(zhǔn)，它的思想非常簡(jiǎn)單，就是對(duì)沒類別下所有劃分的計(jì)數(shù)加1，這樣如果訓(xùn)練樣本集數(shù)量充分大時(shí)，并不會(huì)對(duì)結(jié)果產(chǎn)生影響，并且解決了上述頻率為0的尷尬局面。

1.4.3、樸素貝葉斯分類實(shí)例：檢測(cè)SNS社區(qū)中不真實(shí)賬號(hào)

      下面討論一個(gè)使用樸素貝葉斯分類解決實(shí)際問題的例子，為了簡(jiǎn)單起見，對(duì)例子中的數(shù)據(jù)做了適當(dāng)?shù)暮?jiǎn)化。

      這個(gè)問題是這樣的，對(duì)于SNS社區(qū)來說，不真實(shí)賬號(hào)（使用虛假身份或用戶的小號(hào)）是一個(gè)普遍存在的問題，作為SNS社區(qū)的運(yùn)營(yíng)商，希望可以檢測(cè)出這些不真實(shí)賬號(hào)，從而在一些運(yùn)營(yíng)分析報(bào)告中避免這些賬號(hào)的干擾，亦可以加強(qiáng)對(duì)SNS社區(qū)的了解與監(jiān)管。

      如果通過純?nèi)斯z測(cè)，需要耗費(fèi)大量的人力，效率也十分低下，如能引入自動(dòng)檢測(cè)機(jī)制，必將大大提升工作效率。這個(gè)問題說白了，就是要將社區(qū)中所有賬號(hào)在真實(shí)賬號(hào)和不真實(shí)賬號(hào)兩個(gè)類別上進(jìn)行分類，下面我們一步一步實(shí)現(xiàn)這個(gè)過程。

      首先設(shè)C=0表示真實(shí)賬號(hào)，C=1表示不真實(shí)賬號(hào)。

      1、確定特征屬性及劃分

      這一步要找出可以幫助我們區(qū)分真實(shí)賬號(hào)與不真實(shí)賬號(hào)的特征屬性，在實(shí)際應(yīng)用中，特征屬性的數(shù)量是很多的，劃分也會(huì)比較細(xì)致，但這里為了簡(jiǎn)單起見，我們用少量的特征屬性以及較粗的劃分，并對(duì)數(shù)據(jù)做了修改。

      我們選擇三個(gè)特征屬性：a1：日志數(shù)量/注冊(cè)天數(shù)，a2：好友數(shù)量/注冊(cè)天數(shù)，a3：是否使用真實(shí)頭像。在SNS社區(qū)中這三項(xiàng)都是可以直接從數(shù)據(jù)庫(kù)里得到或計(jì)算出來的。

      下面給出劃分：a1：{a<=0.05, 0.05<a<0.2, a>=0.2}，a1：{a<=0.1, 0.1<a<0.8, a>=0.8}，a3：{a=0（不是）,a=1（是）}。

      2、獲取訓(xùn)練樣本

      這里使用運(yùn)維人員曾經(jīng)人工檢測(cè)過的1萬個(gè)賬號(hào)作為訓(xùn)練樣本。

      3、計(jì)算訓(xùn)練樣本中每個(gè)類別的頻率

      用訓(xùn)練樣本中真實(shí)賬號(hào)和不真實(shí)賬號(hào)數(shù)量分別除以一萬，得到：

      

      

      4、計(jì)算每個(gè)類別條件下各個(gè)特征屬性劃分的頻率

      

      

      0.2|C=0)=0.2" alt="" src="http://latex.codecogs.com/gif.latex?P(a_1%3E0.2|C=0)=0.2">

      

      

      0.2|C=1)=0.1" alt="" src="http://latex.codecogs.com/gif.latex?P(a_1%3E0.2|C=1)=0.1">

      

      

      0.8|C=0)=0.2" alt="" src="http://latex.codecogs.com/gif.latex?P(a_2%3E0.8|C=0)=0.2">

      

      

      0.8|C=1)=0.1" alt="" src="http://latex.codecogs.com/gif.latex?P(a_2%3E0.2|C=1)=0.1">

      

      

      

      

      5、使用分類器進(jìn)行鑒別

      下面我們使用上面訓(xùn)練得到的分類器鑒別一個(gè)賬號(hào)，這個(gè)賬號(hào)使用非真實(shí)頭像，日志數(shù)量與注冊(cè)天數(shù)的比率為0.1，好友數(shù)與注冊(cè)天數(shù)的比率為0.2。

      

      

      可以看到，雖然這個(gè)用戶沒有使用真實(shí)頭像，但是通過分類器的鑒別，更傾向于將此賬號(hào)歸入真實(shí)賬號(hào)類別。這個(gè)例子也展示了當(dāng)特征屬性充分多時(shí)，樸素貝葉斯分類對(duì)個(gè)別屬性的抗干擾性。

1.5、分類器的評(píng)價(jià)

      雖然后續(xù)還會(huì)提到其它分類算法，不過這里我想先提一下如何評(píng)價(jià)分類器的質(zhì)量。

      首先要定義，分類器的正確率指分類器正確分類的項(xiàng)目占所有被分類項(xiàng)目的比率。

      通常使用回歸測(cè)試來評(píng)估分類器的準(zhǔn)確率，最簡(jiǎn)單的方法是用構(gòu)造完成的分類器對(duì)訓(xùn)練數(shù)據(jù)進(jìn)行分類，然后根據(jù)結(jié)果給出正確率評(píng)估。但這不是一個(gè)好方法，因?yàn)槭褂糜?xùn)練數(shù)據(jù)作為檢測(cè)數(shù)據(jù)有可能因?yàn)檫^分?jǐn)M合而導(dǎo)致結(jié)果過于樂觀，所以一種更好的方法是在構(gòu)造初期將訓(xùn)練數(shù)據(jù)一分為二，用一部分構(gòu)造分類器，然后用另一部分檢測(cè)分類器的準(zhǔn)確率。