歐氏距離定義： 歐氏距離（ Euclidean
distance）是一個通常采用的距離定義，它是在m維空間中兩個點之間的真實距離。
在二維和三維空間中的歐式距離的就是兩點之間的距離，二維的公式是
d = sqrt((x1-x2)^+(y1-y2)^)
三維的公式是
d=sqrt(x1-x2)^+(y1-y2)^+(z1-z2)^)
推廣到n維空間，歐式距離的公式是
d=sqrt( ∑(xi1-xi2)^ ) 這里i=1,2..n
xi1表示第一個點的第i維坐標,xi2表示第二個點的第i維坐標
n維歐氏空間是一個點集,它的每個點可以表示為(x(1),x(2),...x(n)),其中x(i)(i=1,2...n)是實數,稱為x的第i個坐標,兩個點x和y=(y(1),y(2)...y(n))之間的距離d(x,y)定義為上面的公式.
歐氏距離看作信號的相似程度。 距離越近就越相似，就越容易相互干擾，誤碼率就越高。
目前該距離也會用于Web2.0的數據相似程度的分析，例如：用戶喜好的相似程度。不過筆者不知道為什么是兩變量的差值平方和？得好好再研究研究
====補充====
網上google一下，終于明白了，看下圖，解釋太明顯了
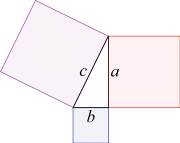
其實就是我們學的最簡單的公式：a
2+b
2=c
2,因此，兩點距離其實就是：sqrt((x1-x2)^+(y1-y2)^)