空間索引
在介紹空間索引之前,先談談什么叫“索引“。對一個數據集做”索引“,是為了提高對這個數據集檢索的效率。書的”目錄“就是這本書內容的”索引“,當我們拿到一本新書,想查看感興趣內容的時候,我們會先查看目錄,確定感興趣的內容會在哪些頁里,直接翻到那些頁,就OK了,而不是從第一章節開始翻,一個字一個字地找我們感興趣的內容,直到找到為止,這種檢索內容的效率也太低了,如果一本書沒有目錄,可以想象有多么不方便…可見書的目錄有多重要,索引有多重要啊!
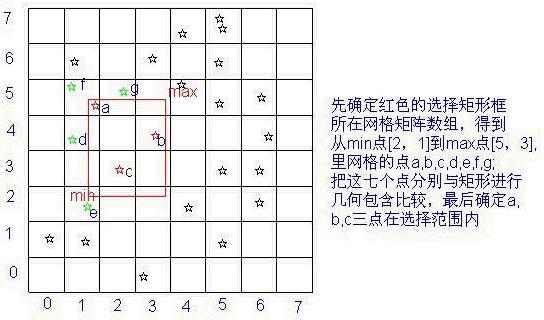
現在大家對索引有了感性認識,那什么是“空間索引“呢?”空間索引“也是”索引“,是對空間圖形集合做的一個”目錄“,提高在這個圖形集合中查找某個圖形對象的效率。比如說,我們在一個地圖圖層上進行矩形選擇,確定這個圖層上哪些圖元被這個矩形所完全包含呢,在沒有”空間索引“的情況下,我們會把這個圖層上的所有圖元,一一拿來與這個矩形進行幾何上的包含判斷,以確定到底哪些圖元被完全包含在這個矩形內。您是不是覺得這樣做很合理呢?其實不然,我們先看一個網格索引的例子:
我們對這個點圖層作了網格索引,判斷哪些點在這個矩形選擇框內,是不需要把這個圖層里所有的點都要與矩形進行幾何包含運算的,只對a,b,c,d,e,f,g這七個點做了運算。可以推想一下,如果一個點圖層有十萬個點,不建立空間索引,任何地圖操作都將對整個圖層的所有圖元遍歷一次,也就是要For循環10萬次;建立索引將使得For循環的次數下降很多很多,效率自然提高很多!
呵呵…想必大家都知道空間索引的好處了,也不知不覺向大家介紹了點圖層的網格索引,還有哪些常用的空間索引呢?這些空間索引又該如何實現呢?帶著這樣的問題,下面介紹幾種常用的空間索引。
網格索引
網格索引就是在一個地圖圖層上,按每個小網格寬△w,高△h打上均勻的格網,計算每個圖元所占據的網格或者所經過的網格單元集合,
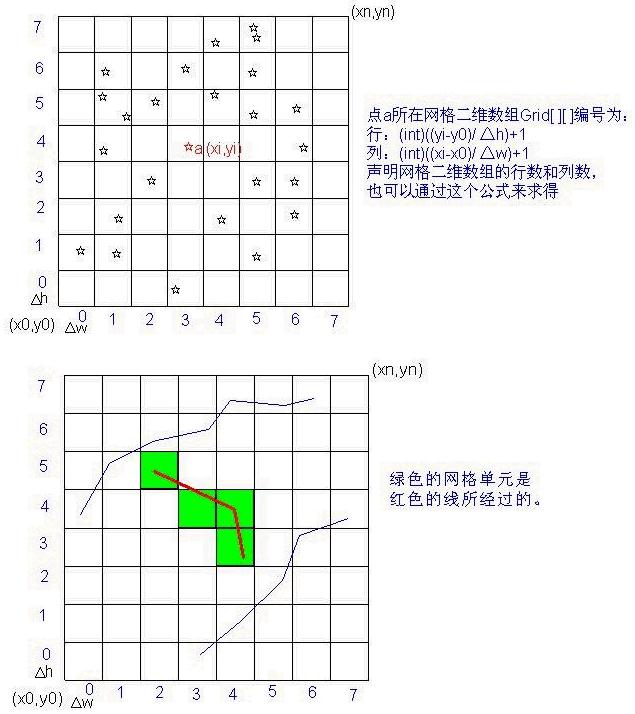
在這些網格單元中,記錄下圖元對象的地址或者引用,比如:聲明一個對象二維數組 List grid[m][n]; m代表網格的行數,n代表網格的列數,每個數組元素為一個“集合對象”,用于存儲這個網格單元所關聯的所有圖元的地址或引用,這樣網格索引就建立好了。下一步,我們該怎么用這個網格索引呢?所有的圖形顯示和操作都可以借助于“空間索引”來提高效率。舉幾個例子來說明“空間索引“的使用:
1,確定所畫矩形左上角和右下角所在的網格數組元素;即可得到這個矩形所關聯覆蓋的所有網格集合;
2,遍歷這個網格集合中的元素,取到每個網格元素List中所記錄的圖元;
3,畫出這些圖元即可。(當然整個過程涉及到兩點:1,屏幕坐標和地圖坐標的互相變換;2,窗口裁減,也可以不裁減)
二、包含判斷,給出一個點point和一個多邊形polygon,判斷點是否在面內,首先判斷這個點所在的網格,是否同時關聯這個polygon,如果不是,表明點不在面內,如果是,可以下一步的精確解析幾何判斷,或者精度允許的情況下,即判斷polygon是包含point的。
另外,Google Map應該也是采用地理網格的方式,對地圖圖象進行索引的,可見一斑,網格索引在圖形顯示,選擇,拓撲判斷上的廣泛應用。但同時也存在很嚴重的缺陷:當被索引的圖元對象是線,或者多邊形的時候,存在索引的冗余,即一個線或者多邊形的引用在多個網格中都有記錄。隨著冗余量的增大,效率明顯下降。所以,很多學者提出了各種方法來改進網格索引,這個將在下面的章節中介紹。而點圖元非常適合網格索引,不存在冗余問題。
四叉樹索引(Quadtree)
類似于前面介紹的網格索引,也是對地理空間進行網格劃分,對地理空間遞歸進行四分來構建四叉樹,本文將在普通四叉樹的基礎上,介紹一種改進的四叉樹索引結構。首先,先介紹一個GIS(Geographic Information System)或者計算機圖形學上非常重要的概念——最小外包矩形(MBR-Minimum Bounding Rectangle):
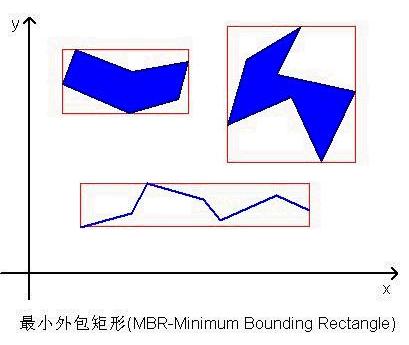
最小外包矩形MBR就是包圍圖元,且平行于X,Y軸的最小外接矩形。MBR到底有什么用處呢,為什么要引入這個概念呢?因為,圖元的形狀是不規則的,而MBR是平行于X,Y軸的規則圖形,設想一下,如果所有的圖元都是平行于X,Y軸的矩形,那針對這樣的矩形進行幾何上的任何判斷,是不是要簡單很多呢?不管我們人自己寫公式算法或者編寫程序運行,是不是都要比原本復雜的圖形幾何運算要簡潔很多呢?答案很顯然。
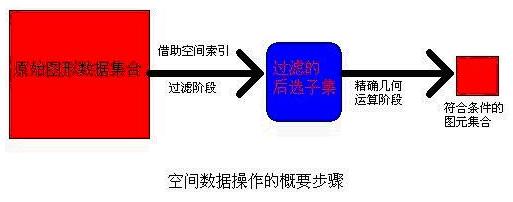
可見,過濾階段,通過空間索引可以排除掉一些明顯不符合條件的圖元,得到后選集合,然后對后選圖元集合進行精確幾何運算,得到最終結果。大家可能會有這樣的疑問,這樣有必要嗎?是不是反而把問題復雜化了?合適的空間索引只會提高計算機的效率,沒有空間索引,我們無疑要對集合中的每個圖元進行精確幾何運算,而這樣的運算是復雜的,是非常占用CPU的,所以需要空間索引,采取少量的內存和簡單的CUP運算,來盡量減少那種高耗CUP的精確運算的次數,這樣做是完全值得的。至于精確的幾何運算到底復雜在哪里,該如何進行精確的幾何運算,將在下面的章節中詳細描述,這里主要介紹過濾階段的空間索引。
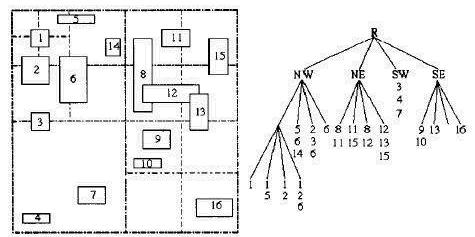
四叉樹索引就是遞歸地對地理空間進行四分,直到自行設定的終止條件(比如每個節點關聯圖元的個數不超過3個,超過3個,就再四分),最終形成一顆有層次的四叉樹。圖中有數字標識的矩形是每個圖元的MBR,每個葉子節點存儲了本區域所關聯的圖元標識列表和本區域地理范圍,非葉子節點僅存儲了區域的地理范圍。大家可以發現,同樣存在一個圖元標識被多個區域所關聯,相應地存儲在多個葉子節點上,比如“6“所代表的圖元,分別存儲在四個分枝上。這樣,就存在索引的冗余,與網格索引存在同樣的弊端。下面我們介紹一種改進的四叉樹索引,或者說是分層的網格索引。
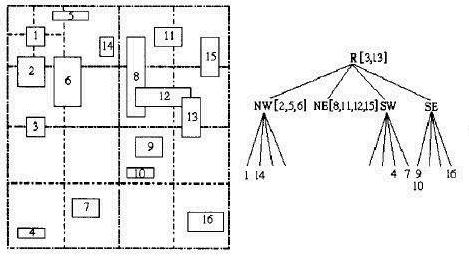
可以看出,3和13分別都跨越了兩個區域,要被一個最小區域完全包含,就只能是根節點所代表的區域,2,5跨越了兩個區域,6跨越了四個區域,要被一個最小區域完全包含,就只能是NW區域。怎么判斷一個圖元被哪個最小區域完全包含呢?從直觀上看,遞歸地對地理空間進行四分,如果圖元與一個區域四分的劃分線相交,則這個圖元就歸屬于這個區域,或者直到不再劃分了,那就屬于這個不再劃分的區域。呵呵。。。可能有點繞口,看圖,結合“最小”“完全包含”這兩個字眼,您就明白了。這顆四叉樹中,圖元的標識不再僅僅存儲在葉子節點上,而是每個節點都有可能存儲,這樣也就避免了索引冗余。同時每個節點存儲本節點所在的地理范圍。
有了四叉樹索引,下面又該如何利用這顆樹來幫助檢索查找呢?還是矩形選擇為例吧!(為什么我總是拿這個例子來說事呢?因為這個例子簡單,容易理解,有代表性!)我們在地圖上畫一個矩形,判斷地圖上哪些圖元落在這個矩形里或者和這個所畫矩形相交。方法很多,這里介紹一種簡單的檢索步驟,如下:
1,首先,從四叉樹的根節點開始,把根節點所關聯的圖元標識都加到一個List里;
2,比較此矩形范圍與根節點的四個子節點(或者叫子區域)是否有交集(相交或者包含),如果有,則把相應的區域所關聯的圖元標識加到List集合中,如果沒有,則以下這顆子樹都不再考慮。
3,以上過程的遞歸,直到樹的葉子節點終止,返回List。
4,從List集合中根據標識一一取出圖元,先判斷圖元MBR與矩形有無交集,如果有,則進行下面的精確幾何判斷,如果沒有,則不再考慮此圖元。(當然,這里只說了一個基本思路,其實還有其他一些不同的方法,比如,結合空間數據磁盤的物理存儲會有一些調整)
總結:改進的四叉樹索引解決了線,面對象的索引冗余,具有較好的性能,而被大型空間數據庫引擎所采用,如ArcSDE,Oracle Spatial等,同時這種結構也適用于空間數據的磁盤索引,配合空間排序聚類,基于分形的Hilbert算法數據組織,將在空間數據格式的定義中發揮重要作用。
posted @ 2009-05-18 09:34 小鋒 閱讀(1850) | 評論 (1) | 編輯 收藏