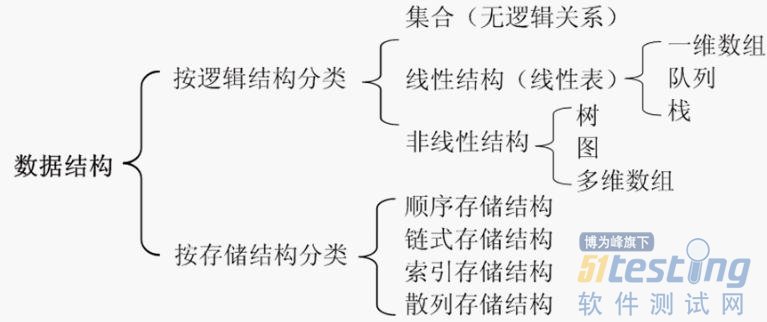
數據結構是計算機存儲、組織數據的方式。常見的數據結構分類方式如下圖：
常用的線性結構有：線性表，棧，隊列，循環隊列，數組。線性表中包括順序表、鏈表等，其中，棧和隊列只是屬于邏輯上的概念，實際中不存在，僅僅是一種思想，一種理念；線性表則是在內存中數據的一種組織、存儲的方式。
順序表
順序表將元素一個接一個的存入一組連續的存儲單元中，在內存物理上是連續的。如下圖：
順序表存儲密度較大，節省空間；但需要事先確定容量，在時間性能方面，讀運算較快，時間復雜度為O(1)；查找運算為O(n/2)，和鏈表同樣；插入運算和刪除運算如果要操作中間一個元素，比如3，那么就需要把3后面的元素全部進行移動，因此時間復雜度相對鏈表要大一些，插入時間復雜度最好為O(0)或最壞為O(n)；刪除時間復雜度為O([n-1]/2)；
鏈表
鏈表擁有很多結點，每個結點前半部分是數據域，后半部分是指針域，指針域指針指向下一個結點；鏈表可分為單鏈表、循環鏈表和雙鏈表。
單鏈表：
從上圖可以看出，單鏈表的上一個結點指針指向下一個結點，最后一個結點的指針域為null。
結點的刪除：
刪除一個結點，如刪除上圖中q結點，只需將p結點中的指針域指向a3，然后將a2釋放掉（free）即可。
結點的插入：
插入一個結點，如插入上圖中s結點，首先將s的指針域指向a2（也就是把s的next賦值為p的next），然后將p結點的指針域指向x即可（p的next指向x）。
循環鏈表與單鏈表唯一不同之處是，循環鏈表的最后一個結點指針不為空，而是指向頭結點。結點的插入和刪除和單鏈表非常相似，就不再示范了。
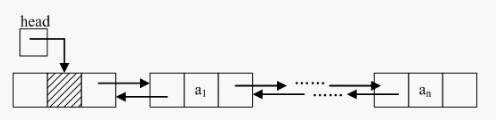
雙鏈表
雙鏈表擁有一前一后兩個指針域，從兩個不同的方向把鏈表連接起來，如此一來，從兩個不同的方向形成了兩條鏈，因此成為雙鏈表。因此，雙鏈表的靈活度要大于單鏈表。
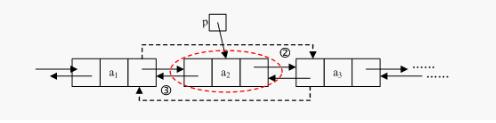
結點的刪除：
雙鏈表的操作比單鏈表要稍顯復雜（按照單鏈表思路來做其實也不難），如上圖，要刪除p節點，首先需要將a1的后驅指向a3，然后將a3的前驅指向a1，最后將p節點釋放掉即可。
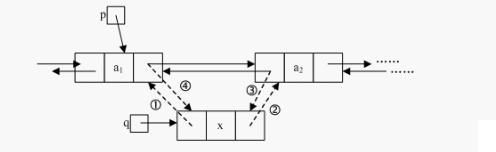
結點的插入：
如上圖，插入q結點，首先要按照方向，將步驟拆分，首先將q節點的前驅指向p結點后驅，緊接著將x后驅指向a2；然后按照順序完成圖中所示的3、4步即可。
從空間性能來看，鏈表的存儲密度要差一些，但在容量分配上更靈活一些。從時間性能來看，查找運算與順序存儲相同，插入運算和刪除運算的時間復雜度為O(1)，要更優于順序存儲，但讀運算則弱一些，為O([n+1]/2)，最好為1，最壞為n。
棧
上面提到棧屬于一個邏輯概念，棧的實現可以用順序也可以用鏈式。它遵循先進后出原則，如下圖：
Java中測試代碼如下：
- package com.snail.test;
-
- import java.util.Stack;
-
- public class TestStack {
-
- public static void main(String[] args) {
-
- Stack<String> stack = new Stack<String>();
- stack.push("NO1");
- stack.push("NO2");
- stack.push("NO3");
-
- System.out.println("初始數量：" + stack.size());
-
- while(!stack.isEmpty()){
- System.out.println(stack.pop());
- }
-
- System.out.println("取完后的數量：" + stack.size());
- }
- }
|
隊列
隊列遵循先進先出的原則，如下圖：
Java中測試代碼如下：
- package com.snail.test;
-
- /**
- *
- * @author Zang XT
- */
- import java.util.Queue;
- import java.util.LinkedList;
- public class TestQueue {
- public static void main(String[] args) {
- Queue<String> queue = new LinkedList<String>();
-
- queue.offer("NO1");
- queue.offer("NO2");
- queue.offer("NO3");
-
- System.out.println("初始數量" + queue.size());
- String str;
- while((str=queue.poll())!=null){
- System.out.println(str);
- }
- System.out.println("取出后數量" + queue.size());
- }
- }
|
運行結果順序為：初始數量3，NO1，NO2，NO3，取出后數量0。
隊列還有一種形式為循環隊列，如下圖：
循環隊列有兩個指針，頭指針head和尾指針tail，尾指針一般指向的不是隊尾元素實際地址，而是指向實際地址的下一個空地址，因此，循環隊列一般犧牲最后一個空間，用來計算該隊列是否滿了，判斷方式是tail+1 = head，既該隊列已滿。
為了盡可能的說清楚，插了大量圖片，希望理解。以后有時間將繼續分析樹、圖等數據結構。