1 最短路徑算法
在日常生活中,我們?nèi)绻枰3M礎(chǔ)地區(qū)和B地區(qū)之間,我們最希望知道的可能是從A地區(qū)到B地區(qū)間的眾多路徑中,那一條路徑的路途最短。最短路徑問題是圖論研究中的一個經(jīng)典算法問題, 旨在尋找圖(由結(jié)點和路徑組成的)中兩結(jié)點之間的最短路徑。 算法具體的形式包括:
(1)確定起點的最短路徑問題:即已知起始結(jié)點,求最短路徑的問題。
(2)確定終點的最短路徑問題:與確定起點的問題相反,該問題是已知終結(jié)結(jié)點,求最短路徑的問題。在無向圖中該問題與確定起點的問題完全等同,在有向圖中該問題等同于把所有路徑方向反轉(zhuǎn)的確定起點的問題。
(3)確定起點終點的最短路徑問題:即已知起點和終點,求兩結(jié)點之間的最短路徑。
(4)全局最短路徑問題:求圖中所有的最短路徑。
用于解決最短路徑問題的算法被稱做“最短路徑算法”, 有時被簡稱作“路徑算法”。 最常用的路徑算法有:Dijkstra算法、A*算法、Bellman-Ford算法、Floyd-Warshall算法、Johnson算法。
本文主要研究Dijkstra算法的單源算法。
2 Dijkstra算法
2.1 Dijkstra算法
Dijkstra算法是典型最短路算法,用于計算一個節(jié)點到其他所有節(jié)點的最短路徑。主要特點是以起始點為中心向外層層擴展,直到擴展到終點為止。Dijkstra算法能得出最短路徑的最優(yōu)解,但由于它遍歷計算的節(jié)點很多,所以效率低。
Dijkstra算法是很有代表性的最短路算法,在很多專業(yè)課程中都作為基本內(nèi)容有詳細的介紹,如數(shù)據(jù)結(jié)構(gòu),圖論,運籌學等等。
2.2 Dijkstra算法思想
Dijkstra算法思想為:設G=(V,E)是一個帶權(quán)有向圖,把圖中頂點集合V分成兩組,第一組為已求出最短路徑的頂點集合(用S表示,初始時S中只有一個源點,以后每求得一條最短路徑 , 就將 加入到集合S中,直到全部頂點都加入到S中,算法就結(jié)束了),第二組為其余未確定最短路徑的頂點集合(用U表示),按最短路徑長度的遞增次序依次把第二組的頂點加入S中。在加入的過程中,總保持從源點v到S中各頂點的最短路徑長度不大于從源點v到U中任何頂點的最短路徑長度。此外,每個頂點對應一個距離,S中的頂點的距離就是從v到此頂點的最短路徑長度,U中的頂點的距離,是從v到此頂點只包括S中的頂點為中間頂點的當前最短路徑長度sat答案 www.jszj123.com
2.3 Dijkstra算法具體步驟
(1)初始時,S只包含源點,即S=,v的距離為0。U包含除v外的其他頂點,U中頂點u距離為邊上的權(quán)(若v與u有邊)或 )(若u不是v的出邊鄰接點)。
(2)從U中選取一個距離v最小的頂點k,把k,加入S中(該選定的距離就是v到k的最短路徑長度)。
(3)以k為新考慮的中間點,修改U中各頂點的距離;若從源點v到頂點u(u U)的距離(經(jīng)過頂點k)比原來距離(不經(jīng)過頂點k)短,則修改頂點u的距離值,修改后的距離值的頂點k的距離加上邊上的權(quán)。
(4)重復步驟(2)和(3)直到所有頂點都包含在S中。
2.4 Dijkstra算法舉例說明
如下圖,設A為源點,求A到其他各頂點(B、C、D、E、F)的最短路徑。線上所標注為相鄰線段之間的距離,即權(quán)值。(注:此圖為隨意所畫,其相鄰頂點間的距離與圖中的目視長度不能一一對等)
圖一:Dijkstra無向圖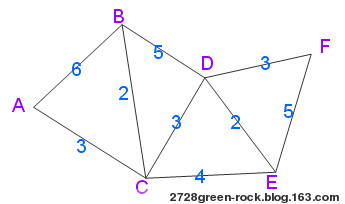
算法執(zhí)行步驟如下表:【注:圖片要是看不到請到“相冊--日志相冊”中,名為“Dijkstra算法過程”的圖就是了】
