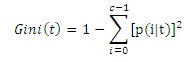轉載請注明出處 http://www.aygfsteel.com/fireflyk/archive/2011/09/25/359447.html
1. 分類
1.1 定義:通過學習得到一個目標函數f,把每個屬性集x映射到一個預先定義的類標號y。
狹隘地說,有大量數據,預先知道所有的類型,但無法分類,通過將數據的多個屬性維度來推測每條數據項屬于哪個類型。(男,高,瘦,帥) -> 極品帥哥,(男,矮,胖,丑) -> 猥瑣男。
嚴格來說,“分類”可以用于描述性建模和預測性建模。
1.2 應用場景
適合預測或描述二元或標稱的,對于序數分類,分類技術不太有效,其他形式的聯系會被忽略。(復習:標稱的,=和≠,教師和工人;序數的,<和>,收入高和收入低)
例如,前幾天看的一個科學研究,個人認為不適合用分類來做。科學家找來志愿者,按臀圍大小分為兩組做智商測試,發現臀圍大的明顯比臀圍小的智商測試結果高。于是得出結論,臀圍大的智商高。我認為,這就是最明顯的一個錯誤,智商高低是序數分類,不能用分類方法來做。它隱藏了一些內在聯系,例如智商高的相對來說愛學習、坐辦公室、少運動導致肥胖、臀圍大。而不是你把臀圍搞大就一定能智商高!
1.3 實現方法
訓練數據 -> 學習模型 -> 模型 -> 應用模型 -> 校驗數據
簡單說就是先訓練,得出結論再校驗。分類方法包括決策樹分類法、基于規則的分類法、神經網絡、支持向量機和樸素貝葉斯分類法。
模型準確率 = 正確預測數 / 總數
2. 決策樹分類
2.1 定義
圖2-1
如上圖,通過提出一系列精心構思的問題,可以解決分類問題,每當一個問題得到答案,后續問題將隨之解決。
根節點、內部節點都是非終結點,是屬性測試條件。葉節點也是終結點,是分類結果。
2.2 建立決策樹
Hunt算法,是許多決策樹算法的基礎,包括ID3,C4.5,CART。
訓練數據集,(Tid, 有房者, 婚姻狀況, 年收入, 拖欠貸款),具體數據見《數據挖掘導論》P94。
大量數據是不拖欠貸款的,所以選取類標號,“拖欠貸款=否”。然后選擇測試條件“有房者”。接下來,再看生成數種,哪個葉子節點是無法確定到類標號的,無法確定的遞歸調用如上步驟,選取測試條件“婚姻狀況”,然后是“年收入”。一棵決策樹建立好了,為何按照這樣的順序?后邊解釋。
測試條件,可以是二元的(男,女),標稱的(單身、已婚、離異),序數的(S號,M號,L號,XL號,分類結果不能是序數的,但是測試條件可以是序數的),連續的(工資是連續屬性)。
2.3 選擇最佳的劃分度量
p(i|t)表示給定節點t中屬于類i的記錄所占的比例,有時候省略t,直接用pi表示。這里介紹不純性(我稱它為區分度,數字越小,區分度越大)度量的一種方法,c是類的個數,
2.3.1 二元屬性劃分
劃分A,結點N1,類C0,4個,類C1,3個;結點N2,類C0,2個,類C1,3個。
|
| N1 | N2 |
| C0 | 4 | 2 |
| C1 | 3 | 3 |
Gini(1) = 1-(4/7)2-(3/7)2 = 24/49
Gini(2) = 1-(2/5)2-(3/5)2 = 12/25
加權Gini = Gini(1) * 7/12 + Gini(2) * 5/12 = 0.486
劃分B,同理得到Gini=0.371,由此說明劃分B更好。
|
| N1 | N2 |
| C0 | 1 | 2 |
| C1 | 4 | 5 |
2.3.2 標稱屬性劃分
與二元屬性(一個屬性,屬性值多元)劃分衡量方法相同,有三元或多元(一個屬性,屬性值多元)的情況,根據計算Gini來決定如何劃分(可以劃分為多路劃分,不局限于兩路劃分)。
2.3.3 連續屬性劃分
把訓練集中每一項都作為一個“<=測試條件”,列出每一個結點下的C0數量和C1數量,計算每一個點的Gini。而事實上,不用每一個點都計算。如《數據挖掘導論》P100中,60,70,75連續且類標號相同,120,125,220連續且類標號相同,所以劃分點選取不能切斷他們,所以這幾個點不用計算Gini值。
2.4 決策樹歸納特點
會有重復的數據碎片,即存在相同兩棵子樹,如圖2-1。
目前為止,每個測試條件只包含一個屬性,對于x1+x2<1,也是可以允許的,稱為斜決策樹。
專注于Java,數據庫性能,Web Server負載,數據挖掘,機器學習等方向